Алфавит языка теории графов.

Разделительные

знаки

Основные символы

Символы объектов

Знаки препинания

скобки

Символы операций

Символы морфизмов и соответствий

a) символика объектов языка теории графов:

Общие символы объектов

Символы сетей, ее видов и типов

Символы объектов

1. C1

2. P1

3. N=<V, ε >

4. M=<U,I>

5. H=<V,E>

Символы элементов V, ε

Индивидуальные символы объектов

1) Icb(v)

2) U={u₁... ul}

3) Ui=<vk,vl>w²

4) ecVk

5) ecV

6) E={e1....ek}

7) U={u1...ut}

8) ε ={e₀, e₁,...e_m}

9) Ui=<vk,vi>V

10) V={v1...vn}

1. On

2. K5

3. K3,3

б=(H |E_j|=2)

1. <V,U,U>

2. <V,E₀,U>

3. <V, U>

4. <V,U>

символы сетей, ее видов и типов

1. общее обозначение сети N=<V,ε>;

2. в том случае, когда Е₀=Ø (Е₀V), то говорят о гиперграфах и записывают H=<V,E>.

Замечание:

1. запись H^’ = <V^’, E^’ > означает, что работают с частью гиперграфа Н: V^’V, E^’E..

2. запись К(Н) означает, что гиперграф Н рассматривают как граф инциденций – двудольный граф с множеством вершин V U E и множеством ребер {<v1,e> : <v2, e> cVE, e E}. Граф К(Н) называют представлением гиперграфа Н.

Матроидом М=<V,I> называют частный случай гиперграфа Н, в котором множество ребер есть независимые подмножества I  B(V), удовлетворяющие условиям:

a) ØI и если AI, BA, то BI.

b) для произвольных А,ВI, таких, что |B|=|A|+1 существует элемент е В\A, такой что AU{e}I. Общим символом для обозначения графов (частный случай гиперграфа) является знак σ, а в том случае, когда необходимо указать, что граф является ориентированным (неориентированным), то пишут:

, где - множество дуг,(U – множество ребер; ). Символ Р_е является обозначением цепи длиной е в гиперграфе Н, а С_е – символ цикла длиной е в Н (С_е есть замкнутая цепь).

Замечание:

1. в графах σ вместо термина цепь используют термины: простой путь σ (для орграфа) и простой маршрут σ (для неорграфа);

2. соответствующие термину «цикл Н» термины в графах: простой контур (для неорграфа) и простой цикл (для орграфа).

Символы элементов сетей V и Е.

• V – символ множества вершин (узлов) сети N, гиперграфа Н, матроида М, графа σ; V={v₁,…v_n}, v_i – вершина (узел).

• ε – символ семейства подмножеств (необязательно различных) множества V, т.е. εV, ε={E₀,E₁,…E_n}={E₀,E}; ;

• U, - символы, соответственно множества ребер (для неографа) и дуг (для орграфа).U={u₁,…u_n}, u_i – ребро, u_i={v_k,v_l}V;

б

Символы сопоставления объектов

) Символы морфизмов и соответствий.

Символы соответствующих элементов множеств

q_v=<V₁,V₂,S>, SV₁xV ₂,

Символы морфизмов μ

<N₁,N₂,m>

Отношение

Отображения Г: V₁ⁿ→V₂

1) N₁N₂

2) <N₁,N₂,Г>

3) <N₁,N₂,Г_f>

<H₁,H₂,m>

<σ₁,σ₂,m>

1) Многозначные отображения <V₁,V₂,Г>

2) Функциональные отображения <V₁,V₂,Г_f>

1) Многозначное отношение <V,R>

2) Функциональное отношение <V,R_f>

1) H₁H₂

2) <H₁,H₂,Г>

3) <H₁,H₂,Г_f>

1) σ₁σ₂

2) <σ₁,σ₂,Г>

3) <σ₁,σ₂,Г_f>

Пояснение к дереву:

- символ изоморфизма объектов (сетей, гиперграфов).

в) Символы операций языка теории графов.

Операции над сетями

Операции композиции над сетями

Операции над сетью (гаперграфом, графом)

-

U

Операции удаления элементов сети



Операция разбиения (гиперграфа, графа)

Операция удаления ребра (дуги)

Операция удаления вершин

Операции над сетью являются способом получения подсети (подгиперграфа, графа) – это т.н. унарные операции. Бинарные операции над сетями являются операциями композиции и служат для образования другой сети (гиперграфа, графа). В читаемом курсе операциями композиции сетей будут операции объединения, пересечения и дополнения.

Гиперграфы.

1) Гиперграф Н – сеть N без выделенных полюсов Е₀, т.е. Н=<V,E>. Для уяснения вводимых понятий рассмотрим пример. Пусть для Н=<V,E> V={v₁, v₂, v₃, v₄, v₅, v₆} E={e₁={v₁}, e2={ v₁, v₃}, e₃={ v₁, v₂, v₃}, e₄=e₅={ v₂, v₄}, e₆={ v₃, v₄, v₅}, e₇=Ø}.

Н

Здесь:

• вершина V₆ называется изолированной;

• ребро е₇ называется пустым ребром:

• ребра е₁,…,е₆ инцидентны своим вершинам;

• вершины, инцидентные ребру, называются смежными (так, v₁ и v₃ инцидентны ребру е₂, являются смежными; являются смежными и вершины v₁, v₂, v₃, т.к. они инцидентны е₃);

• ребра е₄ и е₅ называются кратными ребрами гиперграфа Н.

а плоскости этот гиперграф имеет вид:

Замечание:

а) ребра, для которых e_i  e_j ≠ Ø, называются смежными;

б) число вершин гиперграфа называется его порядком и обозначают |H|;

в) гиперграф Н=<V,E> с мощностью множества вершин |V|=n и мощностью множества ребер |E|=m принято называть (n,m) – гиперграфом (в нашем примере (6,7)).

Отметим, что заданный в примере (6,7) гиперграф можно графически представить как бинарное соответствие:

Здесь:

1) Р – закон сопоставления элементов V и Е.

Так представленный гиперграф H=<(VUE),

{<vi,ej>  VH}> принято называть Кениговым представлением и записывать К(Н).

Очевидно, что это представление можно назвать и графиком инциденций.

2) Гиперграф называют двойственным к гиперграфубез изолированных вершин, если К(Н*)=<E,V,P>

V P  VX E

3) Очевидно (H*)*=H

4) Гиперграф Н=<V,Ø> есть пустой гиперграф. В этом случае такой граф имеет символическую запись О_n, где n=|V| .

5) (n,m) – гиперграф с петлями, т.е. |e_i|=1 называется однородным гиперграфом.

Пример:

e1 e2 e3 e4 e5

v1 v2 v3 v4 v5

6) Отношения смежности есть отношения между вершинами или ребрами, в то время как отношение инцидентности есть отношения между вершинами и ребрами.

7) Всякой прямоугольной матрице из нулей и единиц можно сопоставить гиперграф, для которого указанная матрица есть матрица инцидентности.

8) Число ребер гиперграфа Н, инцидентных данной вершине, называется степенью вершины. В этом случае записывают degv_i=k (так, в нашем примере degv₁=3,degv₆=0, degv₅=1).

9) Число вершин гиперграфа Н, инцидентных данному ребру, называется степенью ребра. В этом случае символическая запись имеет вид deg е_j=|e_j| (так, в нашем примере dege₁=1,dege₃=3, dege₇=0).

10) Гиперграф Н без кратных ребер, степень любого ребра которого равна h, т.е. h=dege_i, называется h-регулярным (h - однородным). Пример:

- триоднородный граф

Замечание:

1. говорят, что регулярный гиперграф представляет h-арное отношение на множестве V.

2. 2-однородный гиперграф с кратными ребрами есть мультиграф.

Пример:

e2

e1 V2

u1 u2

V1 u3 V3

3. 2-однородный гиперграф без кратных ребер есть простой граф. Пример:

e1 V2

e2

u1 u2

V1 V3

4. Гиперграф часто задают и мографом (модельным графом).

Части гиперграфа Н^’ =<V^’,E^’>.

Напоминание:

1. Гиперграф Н_i=<V,E^’> называется частью гиперграфа Н=<V,E>, если Е’E

2. В том случае, когда удалены некоторые вершины из V и инцидентные им ребра гиперграфа Н=<V,E>, то говорят о подгиперграфе Н’ (т.е. в этом случае для Н^’ =<V^’,E^’> V’V, E’E).

3. Подгиперграф Н’, описываемый такой последовательностью инцидентных вершин и ребер - <v₁,e₁,v₂,e₂,…,e_l,v_l+1>, что:

• все вершины кроме, возможно, крайних, различны;

• е₁,…,е_;l – различные ребра;

• v_i,v_i+1e_i i=1,...e называется цепью Р_е длины е.

В этом графе Н:

Р₃=v₂,e₅,v₅,e₄,v₇,e₃,v₈ – цепь длины 3;

Р₂=v₁,e₁,v₂,e₂,v₃ – цепь длины 2.

e5

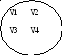
e1

e4

e3

Замечание:

1. если в Р_е е>1 и v_i+1=v₁, то цепь называется циклом С_е=<v₁,e₁,…,v₁,e₁>. В нашем примере С₄=v₂,e₁,v₄,e₃,v₇,e₄,v₅,e₅,v₂ – цикл длины 4; С₅=v₁,e₁,v₂,e₅,v₅,e₄,v₇,e₃,v₄,e₂,v₁ – цикл длины 5.

2. гиперграф не содержит циклов, если его кенигово представление является лесом. Пример:

3. цепь и цикл, если гиперграф является графом (простым графом, мультиграфом), соответственно называется простой цепью и простым циклом. Пример: Для графа σ=<V,u>

u1

v₁,u₁,v₂ простые

v₁,u₁,v₂,u₃,v₄,u₇,v₇ цепи

v₁,u₁,v₂, u₃,v₄,u₂,v₁ – простой цикл

V1 V2 V6

u2 V4 u3 V5

V3 u6

u4 u5

u7 u8

V7 u9 V8

4. в том случае, если последовательности вершин и ребер графа σ=<V,u> все ребра различны, а вершины могут повторяться, то говорят о цепи графа. В нашем примере v₁,u₁,v₂,u₃,v₄,u₇,v₇,u₉,v₈,u₈,v₄ – цепь не является простой;

5. в графе σ говорят о маршруте, если на последовательность вершин и ребер не наложены ограничения;

6. в графе σ говорят о маршруте, если на последовательность вершин и ребер не наложены ограничения;

7. очевидно, что существует биективная функция между цепями (циклами) гиперграфа Н_n,m и его простыми цепями в кениговом представлении К(Н).

Связкость в гиперграфах.

Гиперграф называется связным, если существует цепь Р_е между любыми двумя вершинами v_i,v_jV. В случае связного гиперграфа говорят, что гиперграф Н образует однокомпонентную связкость и записывают это так:

k(H)=1 (для графа Кенига пишут k(K(H))).

Гиперграф Н называется несвязным, если он неоднокомпонентный, т.е. если k(H)>1 (или k(K(H))>1).

Примечание:

a) матрицу М_(D)=||m_ij|| гиперграфа Н М_(D): V×V→{0,1}, для которой

1, если существует цепь из V_i вV_j, V_i≠V_j ,

m_ij= 0, в противоположном случае .

называют матрицей достижимости (связи, связности).

б) все элементы m_ij матрицы достижимости М_(D) для связного неографа равны 1.

в) представление частей гиперграфа и подгиперграфов аналогично представлению гиперграфа. Представление (задание) Н=<V,E> означает задание множества вершин V, множества ребер Е и отношений инцидентности R.

Ниже на вершинах дерева представим широко используемые на практике способы представления графов (частей и подгиперграфов).

Способ представления

Теоретико-множественное задание Н

Матричное представление Н

Представление Н графом инцидентностей

Представление Н списком ребер Е

Представление

σ матрицей смежности

мографом

Представление Н схемой связных обл. плоскости

Представление

σ матрицей Киргофа

Представление Н матрицей достижимостей

Представление Н матрицей инцидентностей

Независимые и зависимые множества гиперграфа.

Множество вершин I B(V) гиперграфа Н называется независимым, если никакие две вершины из этого множества не смежны. Иначе, если I B(V) и I независимы в Н, то порожденный подгиперграф Н’ является пустым, т.е. H’=<V’,Ø> - подгиперграф без ребер (пустой H’).

Замечание:

1. очевидно, что если при этом I’I, то I - тоже независимое множество.

2. подмножества B(V)\I называются зависимыми подмножествами множества V.

3. подмножество ребер I_p B(E) гиперграфа Н такое, что никакие два ребра e_i и e_j из Е не инцидентны одной вершине, называется паросочетанием в гиперграфе Н=<V,E> (или называется независимым множеством ребер в Н).

Иначе, Е’ есть паросочетание для каждых двух ребер e_i, e_j Е’ имеем либо e_i=e_j, либо e_i  e_j=Ø.

Пример (задача о супружеских парах): Пусть Ю и Д – соответственно множество юношей и девушек, и пусть кортеж <x,y> - означает, что юноша х знаком с девушкой у. Тогда парасочетание I_p соответствует возможному множеству супружеских пар, в котором каждая пара образована из юноши и девушки, знакомых между собой, причем каждый человек участвует не более чем в одной паре.

Утверждение:

Всякий гиперграф Н=<V,E> может быть представлен прямоугольной |V|×|E| булевой матрицей инциденций

1, если v_i Е_j ;

μ_n:V×E→ 0, если v_iЕ_j .

Так, матрица инциденций для гиперграфа, представленного выше графически, имеет вид:

	Е1	Е2	Е3	Е4	Е5	Е6	Е7
V1	1	1	1	0	0	0	0
V2	0	0	1	1	1	0	0
V3	0	1	1	0	0	1	0
V4	0	0	0	1	1	1	0
V5	0	0	0	0	0	1	0
V6	0	0	0	0	0	0	0

Замечание1:

Граф Кенига всегда можно представить мографом (модельным графом). В этом случае смежные вершины Н соединяют бинарными ребрами, а при вершинах Н указывают множество смежных ребер {e_i,e_j,…e_l}. Так, для рассматриваемого примера его мограф имеет вид:

V3={e2,e3,e6}

V2={e3,e4,e5}V4={e4,e5,e6}

V1={e1,e2,e3} V6 V5={e6}

Замечание2: Криптографическим представлением гиперграфа Н может быть рисунок. Так для четкого гиперграфа Н имеем:

	е1	е2	е3	е4	е5	е6	е7
v1
v2
v3
v4
v5
v6

e3

e6 V6

V1 e2 e3

e5

e1 V5 e4 V3

V2 V4

Аналогично для нечеткого гиперграфа :

	е1	е2	е3	е4	е5	е6	е7
v1
v2
v3
v4
v5
v6

	е1	е2	е3	е4	е5	е6	е7
v1		0.2
v2	0.3	1					0.9
v3			0.6	0.6	0.6	0.6
v4			1	1	1	1
v5			1			1
v6			0.8			0.8

Здесь список нечетких подмножеств вершин следующий:

E₁={<v₁,0>,<v₂,0.3>,<v₃,0>,<v₄,0>,<v₅,0>,<v₆,0>};

E₂={<v₁,0.2>,<v₂,1>,<v₃,0>,<v₄,0>,<v₅,0>,<v₆,0>};

E₃= E₆={<v₁,0>,<v₂,1>,<v₃,0.6>,<v₄,1>,<v₅,1>,<v₆,0.8>};

E₄= E₅={<v₁,0>,<v₂,0>,<v₃,0.6>,<v₄,1>,<v₅,0>,<v₆,0>};

E₇={<v₁,0>,<v₂,0.9>,<v₃,0>,<v₄,0>,<v₅,0>,<v₆,0>}.

Представление схемой связных областей плоскости этого гиперграфа может следующим:

e3, e6 e2 e2

V6 V1

e7

e1 V2 e4,e5

e3,e6 V5 V3 e3,e6

e4,e5

V4 e3,e6

Замечание3: для графов, помимо матрицы инциденций (которая также может быть весовой) и списка ребер, для обработки на ЭВМ широко используются представления матрицей смежности: μ_с:V×V→A(σ) и матрицей Кирхгофа: μ_k: V×V→B(σ), в которых:

1, если v_i и v_j – смежные вершины графа σ,

a_i,j= 0, если v_i и v_j – несмежные вершины графа σ.

и

-1, если v_i и v_j – смежные вершины графа σ,

в_i,j= 0, если v_i и v_j – несмежные вершины графа σ,

deg v_i, если i=j .

Следует отметить, что в матрице Кирхгофа сумма элементов каждой строки и каждого столбца равны нулю.

Пример:

V={v₁, v₂, v₃, v₄, v₅, v₆};

E={<1,2>,<1,3>,<3,2>,<3,4>,<5,4>,<5,6>,<6,5>}

V2

V5

V1

V4

V6

V3

Задание этого орграфа матрицами смежности, инцидентности и Кирхгофа следующее:

Если граф рассматривать как взвешенный граф направлений:

	v1	v2	v3	v4	v5	v6
v1	2	-1	-1	0	0	0
v2	-1	2	-1	0	0	0
v3	-1	-1	3	-1	0	0
v4	0	0	-1	2	-1	0
v5	0	0	0	-1	2	-1
v6	0	0	0	0	-1	2

	v1	v2	v3	v4	v5	v6
v1	0	1	1	0	0	0
v2	0	0	0	0	0	0
v3	0	1	0	1	0	0
v4	0	0	0	0	0	0
v5	0	0	0	1	0	1
v6	0	0	0	0	1	0

μ_c=

μ_к=

Пример: Для кубического неографа

Матрицы смежности, инцидентности и Кирхгофа следующие:

V3 V4

V1 V6

V1 V5

	1	2	3	4	5	6
1	0	1	1	0	1	0
2	1	0	1	0	1	0
3	1	1	0	1	0	0
4	0	0	1	0	1	1
5	1	1	0	1	0	1
6	0	0	0	1	1	0

μ_c=

	<1,2>	<1,3>	<3,2>	<3,4>	<5,4>	<5,6>	<6,5>
v1	-1	-1	0	0	0	0	0
v2	1	0	1	0	0	0	0
v3	0	1	-1	-1	0	0	0
v4	0	0	0	1	1	0	0
v5	0	0	0	0	-1	-1	1
v6	0	0	0	0	0	1	-1

	<1,2>	<1,3>	<1,5>	<2,3>	<2,5>	<3,4>	<4,5>	<4,6>	<5,6>
1	1	1	1	0	0	0	0	0	0
2	1	0	0	1	1	0	0	0	0
3	0	1	0	1	0	1	0	0	0
4	0	0	0	0	0	1	1	1	0
5	0	0	1	0	1	0	1	0	1
6	0	0	0	1	0	0	0	1	1

μ_и=

	v1	v2	v3	v4	v5	v6
v μк= 1	3	-1	-1	0	-1	0
v2	-1	3	-1	0	-1	0
v3	-1	-1	3	-1	0	0
v4	0	0	-1	3	-1-	-1
v5	-1	-1	0	-1	4	-1
v6	0	0	0	-1	-1	2

Идентификация гиперграфов, заданных своими представлениями.

Будем считать, что гиперграф полностью задан, если все его вершины помечены (в частности пронумерованы). Будем говорить, что гиперграфы Н₁=<V₁,E₁>, Н₂=<V₂,E₂> изоморфны, если существует такая биективная функция (взаимно однозначное соответствие) Гf: V₁→V₂, что для произвольных V_i и V_jV₁ имеем:

(для подмножества заданного множества)

(для упорядоченных подмножеств)

Замечание:

Циклы Н₁ и Н₂ изоморфны, если для них существует биективная функция множеств вершин и множеств ребер, сохраняющее отношения инцидентностей. Обычно изоморфные графы не различают между собой. Так, отвлекаясь от метрических свойств объекта, моделью которого является гиперграф, нет разницы между «мышкой» и «слоном», т.е. с точки зрения теории графов эти объекты изоморфны (это означает, что один и тот же Н можно изобразить по-разному):

Утверждение:

Гиперграфы изоморфны, тогда и только тогда, когда их матрицы инцидентности получаются одна из другой путем соответствующих перестановок строк и столбцов.

Замечание: Аналогичное утверждение можно сделать для:

• матриц смежности изоморфных графов;

• матриц Кирхгофа изоморфных графов.

Для графов σ помимо отношения изоморфизма широко используют отношение гомеоморфизма (не путать с гомоморфизмом). Два графа называются гомеоморфными, если они изоморфны с точностью до вершин второй степени.

Примеры:

a) σ₁=<|V|=4,|u|=6> σ₂=<|V|=6,|u|=8>; б) σ ₁=<|V|=6,|u|=8> σ₂=<|V|=4,|u|=6>

σ₁ гомеоморфен

σ₂

σ₁ гомеоморфен

σ₂

Примечание: Гомеоморфизм и изоморфизм графов является отношением эквивалентности на множестве графов.

Пример: на множестве из 6-ти ниже приведенных графов

построим граф, соответствующий отношению эквивалентности.

Решение:

т.к. отношение эквивалентности на множестве объектов есть совокупность трех свойств – рефлективности, симметричности и транзитивности, то имеем:

Здесь: М₁М={σ₁,σ₂,σ₃,σ₄,σ₅,σ₆}, М_i – множество попарно изолированных графов, т.е. М₁={ σ₁,σ₂,σ₅}. Аналогично М₂М и М₂={ σ₃,σ₄}, М₃М и М₃={ σ₆}. Итак, отношением эквивалентности множество М из 6-ти графов разбивается на три непересекающихся подмножества изоморфных графов М₁М₂=Ø, М₁М₃=Ø, М₂М₃=Ø, M₁M₂M₃=M.

Раскраска гиперграфов.

Раскраска гиперграфов – приписывание цветов вершинам и (или) ребрам гиперграфа, обладающих соответствующими свойствами:

Вершины или (и) ребра гиперграфа можно интерпретировать как раскраску элементов гиперграфа при наложенных требованиях и ограничениях.

Такие задачи часто возникают при проектировании ВС.

Раскраска вершин (ребер) гиперграфа Н=<V,E> называется правильной, если любое ребро е_iE содержит две вершины, окрашенные в разные цвета (если смежные ребра окрашены в разные цвета). Очевидно, что правильную раскраску могут допускать только гиперграфы, каждое ребро которого имеет степень не менее 2, т.е. deg e_i≥2, | e_i |≥2.

Ниже рассмотрим вершинную раскраску гиперграфа без изолированных вершин и | e_i |≥2. Правильную вершинную раскраску Н называют простой раскраской Н.

Гиперграф называют К-цветным, если для него существует правильная раскраска в К цветов (КN).

Хроматическим числом χ(Н) называют наименьшее число цветов, достаточное для правильной окраски гиперграфа Н.

Если χ(Н)=К, то гиперграф называют К-хроматическим.

Операции над гиперграфом и гиперграфами.

Операции над Н=<V,E>

Операция уменьшения числа элементов Н

Операция увеличения числа элементов Н

Операция удаления вершин

Операция добавления вершин в Н

Операция добавления ребер в Н

Расщепление вершин в Н

.....

Операция удаления ребер Н

Операция стачивания ребер Н

Операция перехода к подгиперграфу H’ H

.....

Удаление вершин гиперграфа означает получение подгиперграфа.

Теоретико-множественные бинарные операции над гиперграфами Н_i и H_j есть:

• объединение Н=Н₁UН₂=<V₁,E₁>U<V₂,E₂>=<(V₁UV₂),(E₁UE₂)>

• пересечение Н=Н₁Н₂=<V₁,E₁><V₂,E₂>=<(V₁V₂),(E₁E₂)>

• произведение Н=Н₁×Н₂=<V₁,E₁>×<V₂,E₂>=<(V₁×V₂),(Eсмежные)>,

где <v_i,v_j> V₁×V₂ и < v_k,v_p> V₁×V₂ смежные в гиперграфе тогда и только тогда, когда или v_i=v_k, a v_j,v_p смежные в Н₂, или v_j=v_p, a v_i,v_k смежные в Н₁.

Реализация гиперграфа.

Реализацией гиперграфа Н называется любой граф σ , удовлетворяющий условиям:

• множество вершин гиперграфа Н есть множество вершин графа σ, т.е. |H|=|σ|;

• любое ребро графа σ содержится в некотором ребре гиперграфа Н;

• для любого ребра еЕ порожденный подграф σ(е) является связным.

Говорят, что реализацией ребра еЕ гиперграфа Н=<V,E> является любой связный граф σ_е, число вершин которого есть е V. Поэтому всякая реализация гиперграфа Н является объединением некоторых реализаций всех ребер.

Пример: Пусть Н=<V,E> есть: Для этого гиперграфа реализациями могут быть:

V1 V2 V3 V4 V5

V6 V7 V8 V9

V1 V2 V3 V4 V5

V6 V7 V8 V9

Строгая реализация гиперграфа

А)

Б)

А) нестрогая реализация гиперграфа (т.к. ребра {v8,v4}, {v4,v5}, {v5,v9}, реализующие граф участвуют в реализации двух ребер гиперграфа – е1 и е2)

Задачи построения реализаций часто возникают при топологическом проектировании и изготовлении ИС и печатных узлов. Можно считать, что проектируемый объект (ИС, печатный узел) задается гиперграфом, а его технологическое исполнение – графом, являющимся реализацией заданного гиперграфа. При этом соединять элементы можно произвольным образом, лишь бы граф σ_е обладал наложенными ограничениями, такими, как, например, планарность (т.е. чтобы на плоскости проводники между элементами не пересекались), древовидность (т.е. граф σ_е был деревом – связным графом без циклов).

Пример: пусть для проектируемого печатного узла его моделью является гиперграф такой, что: Н=<V={Э₁, Э₂,Э₃,Э₄}; Е={е₁,е₂,е₃}>, где:

Э1

Э2

Э3

Э4

V1 V3 V6 V11 V8 V9

V2 V5

V4 V10

V7

е₁={Э₁,Э₂}V, е₂={Э₂,Э₄}V, е₁={ Э₁, Э₂,Э₃,Э₄}=V.

Графическое представление заданного гиперграфа Н=<V,E>:

e1 Э1 е1

e2 Э2 е2

Э1 Э3

Э3

e3 е3

Э2 Э4 Э4

Пусть требуется, чтобы реализацией этого гиперграфа был планарный граф, такой, что выводы Э₁, Э₂,Э₃,Э₄ идентичны ребрам е₁,е₂,е₃:

b₃, b₆e₁; b₉, b₁₀e₂; b₄,b₇,b₅,b₈e₃.

Согласно Эйлерову признаку планарности графа |V|-|u|+|Г|=2, где Г – число граней; имеем графовую модель в виде неупорядоченного множества с идентификацией выводов Э₁, Э₂,Э₃,Э₄.

Э1

Э3

V3 u1 V6 u6 e3

V1 V11

V2 V4 V7 Э1 u5 Э3 e1

Э1 Э3

u2 u3

e2

u4 u2

Э2

Э4

V5 V8 Э2 u3 Э4 Э2 Э4

V10 u5 u6 V9

u1

u7

Возможности реализации гиперграфа Н графом  с заданными свойствами (быть деревом, быть планарным графом, быть Эйлеровым или Гамильтоновым графом):

• строгая реализация гиперграфа Н=<V,E> существует тогда и только тогда, когда для любого множества А ребер графа  = <V,u> выполняется неравенство: , гдеE={e₁, e_2….. e_m}; m=|E|, r_i – ранговая функция (функция ранга) матрицы M_i (i=1,m); A V;

• Реализация связного гиперграфа H=<V, E> деревом существует тогда и только тогда, когда граф удовлетворяет условию Хелли, а реберный граф (Н) триангулированный (хордальный);

Пояснение

• Говорят, что множество попарно смежных ребер гиперграфа H=<V, E>, E={e₁, e_2….. e_к} удовлетворяет условию Хелли, если (иначе, если существует по крайней мере одна большая вершина, инцидентная каждому ребру e_i, то гиперграф Н удовлетворяет условию Хелли).

• Граф  = <V,U^~>, разбивающий плоскость на области, ограниченные тремя ребрами. Для max триангулированного графа число ребер равно 3|V|-6.

• Реализация гиперграфа Н плоским графом существует, если граф Н удовлетворяет ослабленному условию Хелли и его реберный граф (Н) – триангулированный.

Пояснение:

Говорят, что граф  = <V,u> плоский, если его можно изобразить на плоскости так, чтобы никакие два его ребра не имели точек пересечения кроме как вершинных. Иначе: граф является плоским, если его можно изобразить без пересечения ребер.

Пример:

Замечание 1

Для всякого представления связного плоского графа без перегородок вершин |V|, число ребер |U| и число граней |Г| (с учетом бесконечности грани) связаны соотношением Эйлера: |V|- |U|+ Г = 2.

Замечание 2

Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Каждая грань максимально плоского графа имеет три вершины и три ребра и потому max-плоский гаф – триангулированный. Говорят, что гиперграф Н удовлетворяет ослабленному условию Хелли, если для любого множества попарно смежных ребер {e₁ , e₂ ….e_k} гиперграф H=<V, E> существуют две такие вершины v₁ , v_i V, что e_i{ v₁ , v_i }0 для каждого i=1,...k

• Реализация гиперграфа Н планарным графом  существует, если реберный граф (Н) гиперграф. Н является планарным.

Жадный (градиентный) алгоритм и матроиды.

Жадный алгоритм – алгоритм решения комбинаторных задач, в котором на каждом шаге возможные в перспективе преимущества приносятся в жертву немедленному приближению к цели.

Утверждение: С помощью жадного алгоритма можно найти независимое подмножество с наибольшим весом.

Пример использования жадного алгоритма.

З

найти такое подмножество из 3-х элементов, чтобы:

- в каждом столбце находилось не более одного выбранного элемента;

- сумма выбранных элементов является наибольшей из возможных.

адача 1

Для матрицы

Решение

У

Напоминание:

Приведенная матрица есть совокупность коэффициентов трех линейных независимых уравнений

e₁ = 7v₁ + 3v₂ + 2v₃

e₂ = 5v₁ + 4v₂ + 3v₃

e₃ = v₁ + 3v₂ + v₃

порядочив каждый из столбцов матрицы А по весу элементов, находи, что I_max3 B(M) равно 15.

Очевидно, что столбцы матрицы А можно трактовать как вектора трехмерного пространства, причем подмножество векторов линейно независимо тогда и только тогда, когда соответствующее им множество столбцов линейно не зависимо.

В этом плане каждая такая матрица порядка mn (m – число элементов в столбце, т.е. число строк матрицы, n – число столбцов матрицы, т. е. число элементов в строке) определяет матроид

M(A)=<V, I>, где V – множество ее столбцов, I – независимые подмножества столбцов таких, что они являются линейно независимыми.

Задача 2

Найти такое подмножество элементов матрицы А, чтобы

- в каждом столбце и каждой строке находилось не более одного выбранного элемента

- сумма выбранных элементов является наибольшей из возможных.

Решение:

Применение жадного алгоритма к матрице А задачи 1 в этой задачи дает подмножество с суммой 12, что не является решением.

Поскольку подмножество

Неправильный результат жадного алгоритма в этой задаче вызван тем, что подобные оптимизационные задачи решаются жадным алгоритмом только для независимых множеств матроида М.

Задача 3 (задача дискретной оптимизации).

Даны конечное множество V, семейство его подмножеств I B(M) и функция W: V R^t. Найти подмножество S  I с наибольшей суммой  W(1)(l S)

Примечание к задаче:

Как Задача 1, так и Задача 2 являются частными случаями этой задачи: в обоих случаях V является н-ом позиций матрицы А, а W ставит в соответствие <I,j> этой матрице число a_ij . При этом для Задачи 1 факт S  I означает, что каждый столбец содержит не более одной позиции из множества S, а для Задачи 2 это означает, что каждый столбец и каждая строка содержат не более одной позиции из множества S  I.

Ответ на вопрос:

«При каких условиях относительно семейства I жадный алгоритм правильно решает оптимизационную задачу для произвольно функции W»

следующий:

комбинаторный объект <V,I> должен быть матроидом M=<V,I>.

Именно в этом случае жадный алгоритм имеет шаги:

1-ый: найти такой элемент v₁V, что W(l₁){l}I

.

.

k-ый (k  2): найти такой элемент e_k  V, что W(e_k)=maxW(l){e₁,...,e_k-1,e_k}I, e ≠e_i, i = 1,...k-1

Если такого элемента нет, то конец.

Замечание

Примером жадного алгоритма является алгоритм Краскала (нахождение остовного дерева максимального веса на ребрах взвешенного графа).

Матроид.

Матроид – гиперграф, определяемый заданием множества V элементов и семейства I независимых подмножеств, т.е. M=<V,I>, где I={I₁,...I_k},I V, аксиомы которых следующие:

- пустое множество  не зависимо;

- каждое подмножество независимого множества независимо;

- для всякого подмножества B I все независимые множества матроида, содержащиеся в B и являющиеся максимальными по включению относительно B, имеют одинаковое число элементов.

Пример

Множество V строк произвольной прямоугольной матрицы порядка mn и семейства I всех подмножеств множества V, составленных из линейно-независимых строк, образуют матроид.

Напоминание

1. Пустой гиперграф H=<V,> есть свободный матроид M=<V, I>

2. Тривиальный матроид М=<V,> есть частный случай гиперграфа с множеством вершин V и одноэлементными подмножествами вершин, где одноэлементное подмножество есть цикл.

Теорема:

Если M=<V,I> есть матроид, то множество S, найденное жадным алгоритмом, является независимым множеством с наибольшим весом. Если же M=<V,I> не является матроидом, то существует такая функция W: V R^t, что S не будет независимым множеством с наибольшим весом.

Замечание:

Мощность максимально зависимого подмножества CV матроида M=<V,I>, называется рангом матроида и обозначается P(C)=max {|A| : a  I^A  C}

Очевидно:

1. что каждые две базы матроида имеют одинаковую мощность

2. что подмножество CV является независимым тогда и только тогда, когда |P(C)|=|C|

Замечание

Матроиды M₁=<V₁,I₁> и |M₂=<V₂,I₂>| изоморфны, т.е. M₁ M₂ если : V₁V₂ - биекция и для любого x V₁ имеется (x) I₂ тогда и только тогда, когда x I₁.

Отметим, что:

1. процесс преобразования матрицы А, реализуемый жадным алгоритмом, это не что иное, как известный из численного анализа метод исключения Гаусса.

2. По окончании работы жадного алгоритма множество S содержит номера ненулевых столбцов – эти столбцы линейно независимы, т.к. после соответствующей перестановки строк они содержат подматрицу размера |S||S| с нулями выше главной диагонали и ненулевыми элементами на диагонали.

Псевдографы.

Гиперграф Н, степени ребе которого deg l_i2 называется псевдографом . В понятие псевдограф включаются понятия: «простой гаф», т.е. 2-однородный гиперграф Н; «нуль-граф» (граф пустого отношения, вполне несвязный граф) – т.е. «тривиальный (пустой) гиперграф» Н; «мультиграф» - гиперграф с кратными ребрами Н такой, что степень каждого его ребра равна 2

(т.е. deg l_i=2); «граф тождественного отношения» - гиперграф Н, все ребра которого – одноэлементные подмножества вершин V.

Графическое представление приведенных понятий может быть следующим:

Примечание

1. рассматриваемые в курсе псевдографы представлены следующей схемой:

2. взвешенный псевдограф в приложениях часто называют направленным (сигнальным) графом, а неограф – линейным (структурным) графом.

Исходные понятия четных псевдографов.

Согласно Бурбаки, граф определяется формулой, гдеV – множество вершин графа ,- множество дуг графа. В этом определении графаисключаются изолированные вершины, поскольку в определение не включается множество вершинV, которое порождает кортежи VV.

Описание графа в смысле Бержа и Кенинга устраняет возможные недоразумения в определении понятия псевдограф с изолированной вершиной. Граф , в смысле Бержа, описывается как соответствиеS между подмножествами V.

Пример:

Sv₁ = {v₂, v₃, v₄}, Sv₂ = {v₁}. Имеем: Sv₃ = , Sv₄ = {v₄}, Sv₅ = {v₃}.

Дополнением графа  называется граф такой, чтои, т.е  и есть разбиение декартова произведенияVV на две части.

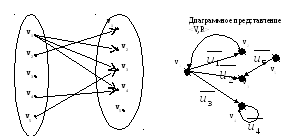
Граф  в смысле Конига описывается как отношение инцидентности и часто называется бихроматическим (двудольным) графом.

Пример:

Пусть представлен в виде двудольного графа <V,U,K> вершин и ребер, такой, что

ему соответствует гиперграф Н и граф  в виде диаграммы:

Замечание

Неограф может рассматриваться как орграф, все дуги которого нестрого параллельны. Примером такого представления может служить схема метрополитена, где двустороннее движение электропоездов отображается ребрами – участниками линий между станциями – вершинами.

Смешанный граф есть множество, на котором заданыU и .

Пример

Степень вершин орграфа degVi есть сумма полустепеней захода и исхода дуг, т.е. .

Среди инцидентных ребер (дуг) псевдографа различают следующие вершины: граничные, висячие, начальные, конечные, внутренние, изолированные, голые, точки сочленения.

Пример

транзитивным замыканием в орграфе называется множество вершин, в которые можно прийти изVi по некоторому пути.

Пример

Пусть

Формально

Орграф называют сильно связным, если (, т.е для любых двух вершин такого графа существует путь, идущий из одной вершины в другую.

Пример:

этот граф сильно связный, а следующий граф не является таковым:

очевидно, что:

1. связный неограф всегда сильно связный

2. бинарное отношение и существование пути из Vi b Vi в орграфе является отношением частичного порядка на множестве вершин V, т.к. оно рефлексивно и транзитивно.

3. Бинарное отношение существование пути из Vi b Vi и наоборот есть отношение эквивалентности, т.к. оно рефлексивно, симметрично и транзитивно.

Подграф ’ графа <V,Г> называют максимально сильно связным, если не существует сильно связного графа ”, строго содержащего’.

Классы графов специального вида.

- Уникурсальный граф – граф, все дуги (ребра) которого составляют простой путь (маршрут) или простой цикл (контур).

- Двудольный граф (бихроматический граф) - граф, в котором можно выделить такие два подмножества V1 и V2 вершин V , что V1V2=V, V1V2= и q=<V1,V2,S>

Пример:

- Дерево ( прадерево) – связный неограф (орграф) с наименьшим числом ребер (дуг); иначе связный граф без циклов, в котором |U|=|V|-1 называется деревом.

Пример:

очевидно, что любое дерево (прадерево) посредством раскраски вершин в два цвета можно представить двудольным графом.

- Лес – несвязный граф, компонентами которого являются деревья. Очевидно, что лес, состоящий из к деревьев, имеет в точности U=|V|-k ребер (дуг).

- Сепарабельный (односвязный, разделимый) граф – связный граф, имеющий хотя бы одну точку сочленения или мост (вершина, удаление которой превращает связный граф в несвязный, называется точкой сочленения, ребро с таким же свойством называется мостом)

Пример:

очевидно, что несепарабельный (неразделимый) граф – связный граф без точек сочленения, означающее, что удаление любой его вершины не нарушает связности нового графа.

- Однородный (регулярный) неограф степени к – граф, степени вершин которого одинаковы.

П

- Полный неограф – однородный граф, все вершины которого попарно смежны. Для этого графа degVi=|V|-1, а число его ребер равно (|V|(|V|-1))/2, т.е. двудольный граф называется полным, если |U|=|V1||V2|.

- Турнир – орграф, если каждые две вершины соединены одной и только одной дугой (иначе, если основанием орграфа является полный неограф).

-Плоский граф – граф, ребра (дуги) которого не пересекаются нигде, кроме инцидентных им вершин.

Планарный граф – граф, изоморфный плоскому графу.

ример:

Замечания:

Достаточным признаком планарности графа является выражение .

Графы, отличающиеся только нумерацией вершин, называются изоморфными.

Разбиение плоскости плоским графом на отдельные области (грани) называют плоской картой. В этом случае критерием планарности связного графа является формула Эйлера |V|-|U|+|Г|=2, где|Г| - число граней карты, включая внешнюю вершину.

О планарных графах говорят, что они имеют плоскую укладку (укладываютя на плоскость).

- Триангулированный граф – максимально планарный граф, т.е. когда при добавлении одного ребра граф перестает быть плоским.

Замечание:

Плоская карта триангулированного графа есть множество граней, ограниченных тремя ребрами (в этом случае плоскую карту называют триангулированной).

Число ребер и граней плоской триангуляции с |V| вершинами равно соответственно |U|=3(|V|-2) и |Г|+2(|V|-2).

- Минимально неплоский граф – неплоский граф, удаление любого ребра которого делает граф плоским.

Пример:

Отметим, что приведенные максимально неплоскостные графы К₅ и К₃₃ лежат в основе теоремы Понтягина – Куратовского: «Граф плоский тогда и только тогда, когда он не сожержит подграфа, гомеоморфного графу К₅ и К₃₃».

- Граф гамильтонов – граф, в котором имеется простой цикл, содержащий каждую вершину этого графа.

Пример:

не гамильтонов граф

гамильтонов граф

- Эйлеров граф – граф, в котором имеется цикл со всеми ребрами графа

Пример:

Эйлеров граф

не Эйлеров граф

- Экстремальный граф – граф, на котором та или иная характеристика принимает свое максимальное или минимальное значение.

Пример: Пусть расстояние между объектов задано матрицей

	V1	V2	V3	V4
V1	0	40	70	90
V2	50	0	90	80
V3	80	50	0	40
V4	70	60	30	0

Требуется определить связный граф такой, чтобы сумма всех весов ребер была минимальной.

Решением этой задачи является экстремальное покрывающее дерево, построенное по алгоритму Краскала – действуя поэтапно, выбирают каждый раз из матрицы ребро с возможно меньшим (большим) значением, добавление которого к уже выбранным ребрам не должно приводить к циклу (в противном случае это ребро отбрасывается).

Имеем:

а) дерево минимального веса;

б) дерево максимального веса; _

Дополнительный граф графа б =<V,U> - граф б =<V,U^*>, множество дуг (ребер) графа U^* которого есть разность множества дуг (ребер) полного графа б=<V,V²> и графа б=<V,U>, т.е. U^*=V²\U

- Граф случайный – граф, ребра и вершины которого могут присутствовать или отсутствовать с определенной вероятностью.

Пример: граф случайный есть вероятная модель ВС, у которого элементы, описываемые вершинами и ребрами, в процессе работы может отказывать и восстанавливаться случайным образом. Показателями такой вычислительной сети могут быть показатели надежности, также как вероятность связности сети в целом, вероятность связности пары выбранных вершин, и т.д.

Части графов.

Граф б΄=<V,U΄> называют частью графа б=<V,U>, если U΄U . Граф б΄=<V΄,U΄>, в котором V΄V, U΄U, называется подграфом графа б=<V,U>. Граф, часть графа <V,U΄> называется суграфом (покрывающим деревом), если удаление некоторых ребер графа <V,U> делает его деревом.

- Разрезом Р связного графа б=<V,U> называется подмножество ребер U΄U, при удалении которых граф распадается на две или больше компоненты связности. Разрез называется простым, если никакое собственное подмножество его ребер не является разрезом данного графа.

- Гамильтонов путь – путь, содержащий все вершины графа U, в котором никакая другая вершина не встречается дважды, а число дуг на единицу меньше числа вершин графа.

Очевидно, что Гамильтонов контур (цикл) – гамильтонов путь, если начальная вершина совпадает с конечной.

- Путь называется простым, если никакая дуга не встречается в нем дважды, и составным в противном случае.

- Путь называется элементарным, если все вершины не встречается дважды, и неэлементарным в противном случае.

- Контур называется элементарным, если все вершины, через которые он проходит в графе б, различны (за исключением только начальной и конечной, которые совпадают).

- Контур называют простым, если все его дуги различны.

Пример:

Пусть <U₁,U₈,U₄,U₅> - простой элементарный путь, путь <U₆,U₇,U₄,U₅> - простой и неэлементарный, путь <U₃,U₄,U₆,U₇,U₄,U₅> - составной и неэлементарный, контур <U₆,U₇,U₄> - простой и элементарный, контур <U_1,U₂,U₅,U₆,U₇,U₄,U₅> - составной и неэлементарный.

- Эйлеровым путем в графе называется простой путь из всех дуг этого графа. Очевидно, что если начальная вершина Эйлерова пути совпадает с конечной вершиной, то такой путь называется Эйлеровым циклом.

Пример: В этом графе <U_1,U₂,U₅,U₄,U₂,U_3,U₄,U_5,U₆> - Эйлеров цикл.

В этом графе нет Эйлерова цикла, но есть Эйлеров путь <U_1,U₂,U₃,U₄,U₁,U_5,U₆,U₃>.

В этом графе существует два эйлерова пути, но нет эйлеровых циклов.

А в этом графе нет ни эйлеровых путей и циклов.

- Подграф называется регулярным степени k, если степень каждой его вершины равна k (т.е. deg V_i=k).

Специфические способы представления графов.

Напомним, что помимо теоретико-множественного задания графов, как бинарных отношений на множестве V, широко используются матричные способы (матрицей инцидентности, матрицей Кирхгофа, матрицей достижимости), списочные (списком вершин, матрицей ребер).

Ниже рассмотрим некоторые другие способы представления сигнальных графов и деревьев.

а) сигнальные графы, соответствующие различным формам записи линейных уравнений.

I. Граф Мейсона (М-граф). М-граф соответствует системе уравнений: xi=∑_j=1ⁿt_ijx_j+∑_m=0^kb_imy_m (i=1,n).

Пример: построим граф б для системы линейных уравнений:

a₁x₁+a₂x₂=(B₁+B₂)y₁

c₁x₁+c₂x₂=0

d₁x₃+d₂x₂=0

g₁x₁+f₁x₃+f₄x₄=0

Решим первое уравнение относительно x_1: x₁ = a₂x₂+(b₁+b₂)y₁ (1) , где a= -a₂/a₁, b₁= B_1/ a_1, b₂₌B_2/ a_1.

Аналогично, разрешая второе уравнение относительно x₂, имеем:

X2=cx1 (2) , c=-c1/c2

x3=dx2 (3) , d=d2/d1

x4=fx3+qx1 (4) , f=f1/f4, g=q1/f4.

Для уравнения (1) имеем взвешенный ортграф б1:

Поскольку уравнение (2) нее содержит новых вершин, то граф, соответствующий уравнениям (1) и (2):

Добавляя вершины х3 и х4 для уравнений (3) и (4), получаем граф системы из четырех линейных уравнений:

В этом графе y1–исток, х4–сток.

Замечание: для построения графа по системе уравнений каждое из них можно разрешить по-разному, что означает, что для системы уравнений возможны различные, но не равновесные графы.

II. Граф Коутса (к-граф) и нуль-граф (N-граф).

К-граф и N-граф соответствуют системе уравнений:

∑_j=1ⁿt_ijx_j-∑_m=0^kl_imy_m =0 (*) (i=1,...n). На N-графе в отличии от М-графа и К-графа, помимо вершин х, y вводятся вершины N_i ,соответствующие нулям уравнения (*)

III. б) задание дерева диаграммой Венна, кодом и символом.

1. Диаграмма Венна дерева Т:

Пример:

Его диаграмма Вена

2. Двоичный код дерева Т.

Дерево Т можно представить двоичным кодом длины 2|U|, если считать направление вдоль ребра по левой стороне за 0, а в противоположном направление – 1.

Пример:

имеем 001001010111

3. Символ дерева Т:

Утверждение: «Любому дереву Т можно поставить во взаимно-однозначное соответствие некоторый символ – упорядоченную последовательность |V|-2 номеров вершин этого дерева (Т)= , среди которых могут быть и повторяющиеся номера вершин».

Получение символа α(Т), и построение дерева Т по его символу осуществляется с привлечением алгоритмов Пруфера.

а) если задано дерево Т с помеченными номерами вершин, то согласно алгоритму Пруфера, процедуры получения символ α(Т) следующие:

- выбираем висячие вершину с наименьшим номером;

- удаляем эту вершину вместе с инцидентным ей ребром и записываем первую компоненту символа номером второй вершины отброшенного ребра;

- повторяем последовательно приведенные процедуры для заданного дерева до тех пор, пока не останутся две висячие вершины, связанные между собой ребром.

Пример:

|V|=11

(Т) = <5,3,1,3,5,5,3,1,1>

б) если задан символ дерева, то построение дерева означает восстановление по компонентам символа висячих вершин и ребер.

Алгоритм Пруффера.

- находим наименьшее число натурального ряда N={1,2,3,...,|V|}, которое не встречается в символе α(Т).

- найденный номер вершины соединяем ребром с вершиной, которая записана в символе дерева первой.

- удаляем номер найденной вершины в пункте 1 из натурального ряда и первый номер из символа (фиксируем N΄N, α(Т)΄α(Т) ).

- повторяем последовательность 1-3. (Пары чисел, оставшиеся в натуральном ряде являются ребром искомого дерева).

Пример: α(Т)=(5,3,1,3,5,5,3,1,1)

Очевидно, что этот символ отображает дерево Т с числом вершин |V| на две больше, чем чисел в символе, т.е.

записываем N=<1,2,3,4,5,6,7,8,9,10,11>.

Наименьшее число, соответствующее в α(Т) – число 2.

Соединяем вершину с номером 2 с вершиной 5 (с первым номером в дереве):

После этого записываем ряд N΄=<1,3,4,5,6,7,8,9,10,11> и α΄(Т)=<3,1,3,5,5,3,1,1>. В N΄ отсутствует номер 2, а в α΄ - номер5.

Наименьшее число ряда N΄, отсутствующее в α΄(Т) -4.

Соединяем ребром вершины с номерами 4 и 3, и т.д.

Замечание:

1. Для изоморфных деревьев с разной нумерацией вершин соответствующие символы различны

2. Символ α(Т) иногда называют кодированием в алфавите обозначения вершин покрывающего дерева.

Основные теоремы, леммы и критерии теории графов.

Теоремы, отражающие свойства графов, рассмотрим в следующей последовательности:

Леммы и теоремы о вершинах и ребрах графа.

1. Лемма о рукопожатиях.

В связном графе = <V, U > сумма степеней всех его вершин – четное число, равное удвоенному числу ребер графа:

_|V|

degV_i = 2|U|

_i=1

Частные случаи:

• для однородного связного графа степени 2: |V| = |U| имеем колесо;

- для полного графа: |V| |V-1| = 2U;

2. В связном орграфе  = <V,U > сумма полустепеней всех его вершин равно числу дуг графа:

_{|V| |V|}

deg⁺V_i = deg ^-V_i = |U|

_{i=1 i=1}

Следствия из леммы о рукопожатиях:

1. Число вершин нечетной степени любого связного графа – четно

2. Число вершин кубического однородного графа всегда четно 3|V| = 2|U|

3. Во всяком графе с числом вершин |V|  2 найдутся по меньшей мере 2 вершины с одинаковыми степенями.

4. Если в графе с числом вершин |V| > 2 в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени «0» , либо в точности одна вершина степени |V-1|