Напоминание: Следует различать в понимании объектный язык (предметный) и метаязык.

Объектный язык – язык, который изучается; метаязык – язык, с помощью которого изучается объектный (в нашем случае русский язык, графы, метаформулы и т.д.).

Пример:

(x U y), ((x U y)∩z) – формулы объектного языка, но формулы U_j=1ⁿx_j и ∩_j=1ⁿx_j – метаформулы (т.е. сокращенная запись: (…(х₁U х₂)U х₃)U…U х_n)…), (…(х₁∩ х₂)∩ х₃)∩…∩ х_n)…)).

Очевидно, что для множества целых чисел Z, как реляционной системы, ε=1. Отметим здесь же, что всякое дискретное множество М счетно (т.е. |M|=|N| - все элементы М можно пронумеровать элементами N), однако не всякое счетное множество дискретно (так множество {1,1/2,1/3,…,1/n,…} является счетным, но не дискретным, т.к. с номером n  N расстояние между соседними элементами стремится к нулю).

Символы правил сопоставления А₃.

1.1 Общие символы для обозначения правил соответствия элементов 2^x множеств.

• если некоторые элементы одного множества М₁ сопоставляются некоторым элементам другого множества М₂ по тому или иному правилу (обозначают символом S), то говорят о соответствии q=<M₁,M₂,S>, где SM₁× M₂ (запись q_~=<M₁,M₂,S_~> означает нечеткое соответствие)

• Если все элементы первого множества сопоставляются некоторым элементам второго множества по какому-то правилу, то говорят об отображении Г элементов первого множества. Запись в этом случае имеет вид: q=<M₁,M₂,Г> (или Г: М₁→М₂).

• В том случае, когда отображение Г является функциональным (однозначным), то используя символ , записываютq=<M₁,M₂,Г_f> ( или Г_f : М₁→М₂)/

• Символ отношения R используют, когда сопоставляются элементы одного и того же множества, т.е. когда М₁=М₂. Факт сопоставления элементов множества М записывают парой <M,R>.

• Если отношения R функционально (однозначно), то для его обозначения принимают символ f, т.е. q=<M,R_f>=<M,f>.

С целью более быстрого усвоения языка теории множеств поясним исходные его выражения.

Графическое пояснение:

S Г q=

X

Сопоставление двух алгебраических систем по тому или иному правилу M обозначают символом μ, т.е. μ=< M₁,M₂,M> и называют морфизмом двух алгебраических систем.

2.2 Индивидуальные символы для обозначения правил сопоставления 2-х множеств.

Индивидуальными (именными) знаками отношений являются символы:

,,,,,,,,,,,, которые означают:

- символ принадлежности элемента множеству (пример записи хМ);

- символ не принадлежности элемента множеству (хМ);

() - символ строгого включения (не включения) подмножества во множество;

() - символ равносильности (не равносильности) множеств (языковых выражений);

() - символ нестрогого включения (не включения) одного множества в другое;

,,,- символ отношений строго меньше, строго больше, меньше и больше.

Символы операций А₂.

2.1 Общие символы для обозначения операций теории множеств.

Символ , где i – арность операции, а j – индекс (номер) операции

будет использоваться для обозначения произвольной алгебраической операции.

Пример:

- унарная операция (т.е. : М→М);

- бинарная операция (т.е. : М² →М).

Для неалгебраической операции будем использовать символ σ.

Замечание:

В том случае, когда нет акцента на арность операции, то будем использовать символ f только с индексом.

2.2 Индивидуальные символы для обозначения операций теории множеств.

• Символ X принят для обозначения неалгебраической теоретико-множественной операции полного (декартового) произведения (пример M₁× M₂).

• Символы ,,\,–,соответственно обозначают алгебраические операции объединения, пересечения, разности, дополнения и прямой суммы на множестве всех подмножеств заданного множества.

Языковые выражения теории множеств.

Правильно построенным языковым выражением будем считать инфиксное, т.е. такое, как показано ниже.

• Запись хМ означает, что элемент х является элементом множества М.

Выражение х={a₁, a₂, a₃ } означает, что элемент х является множеством из 3-х элементов.

• Формулы МХ,YZ, AUB=M, K= M₁∩ M₂, M₃\M₄=P, М читаются, соответственно как: М есть собственное подмножество множества Х, что аналогично выражению МХ, но МХ; множествоY есть несобственное подмножество множества Z; М есть объединение множеств А и В; множество К есть пересечение множеств M₁ и M₂; множество Р есть разность множеств M₃ и M₄; множество М есть дополнение множества М.

• Выражение М=Х трактуется как представление одного и того же множества разными символами и аналогично тому, что МХ и ХМ.

• Понятие мощности множества (расширение понятия числа элементов конечного множества на бесконечное) записывается с помощью прямых скобок: |M|=n – множество М содержит n элементов, т.е. М={x₁, x₂,…, x_n}. |X|=|N| - множество Х равномощно множеству всех натуральных чисел. |D|>|N| - мощность множества всех действительных чисел больше мощности множества всех натуральных чисел. |Q|< |Y| - мощность множества рациональных чисел меньше мощности множества Y.

• Запись М=Ø аналогична записи |M|=0.

Примечание 1:

Префиксные и постфиксные записи языковых выражений теории множеств будем использовать как сокращенные способы записи больших выражений.

Способы задания множеств

Перечислением элементов множеств

Описание элементов

Описание характеристических свойств множеств

Описание множеств, порожденных процедурами над элементами

• Задание множеств перечислением его элементов принято для конечных множеств небольшой мощности или для бесконечных множеств, когда ясно, что понимается под таким множеством.

Пример 1. N = {1, 2, 3, …}

Пример 2. Спецификация cборочного чертежа печатного узла задаёт перечислением множества ЭРИ и конструктивов.

Пример 3. Множество M = {x, y, z} состоит из трёх элементов, порядок перечисления которых не имеет значения, т.е. {x, y, z} = {y, x, z} = … = {z, y, x}

• Описание множества характеристическим свойством его элементов означает наличие этого свойства у каждого из них.

Пример 4. М = {x  N: 1 ≤ x < 5}, u=N.

Эта запись (читается: множество M состоит из элементов х, принадлежавших универсуму N таких, которые больше или равны 1 и меньше 5, аналогична заданию множества M перечислением его элементов: М = {1, 2, 3, 4}.

Пример 5. Множество M = {x²  N; x – простое число} задано квадратами простых чисел.

Пример 6. Множество корней уравнения х² – 1 = 0 для u=Z и u=N имеет следующее описание: M₁ = {x  Z: x² – 1 = 0}={-1;1}; M₂={xN:x²-1=0}={1}.

Пример 7. Задание множества М как множества кортежей таких, что M = {< x, y>  D²: x+y = 3} аналогично его заданию в виде М = {x  D, y  D: x + y = 3}

Пример 8. Множество рациональных чисел Q способом описания можно представить так: Q = {<x,y>  Z²: x/y, x  Z, y  Z \ {0}}, т.е. Q есть множество всех целых чисел, дробных (положительных и отрицательных) и нуля.

Пример 9. Декартово произведение A  B = {<a,b>: a  A, b  B} представляет множество пар таких, что первая компонента принадлежит множеству A, а вторая - множеству B.

Пример 10. Теоретико-множественные операции на универсальном множестве U можно записать c агрегатной и атрибутивной точек зрения так:

A=xU: xA, А=(х<= u)→(x<A)

AB=xU: xA или xB, AUB=(x<=A)V(x<=B)

A∩B=xU: xA и xB, A∩B=(x<=A)Λ(x<=B)

A\B=xU: xA и xB, A\B=(x<=A) Λ(x<B)

AB=xU: xA\B и xB\A, AB=(x<=A\B) Λ(x<=B\A)

• Заданные множества с помощью порождающей процедуры, означает указание алгоритма порождения элементов этого множества.

Пример 1:

Основные теоретико-множественные операции с нечеткими подмножествами, заданного универсума можно описать так:

A_~B_~=xU: f_A~ B_~(x)= max (f_A~ (x), f_B~ (x)),

A_~∩B_~=xU: f_A~ ∩ B_~(x)= min (f_A~ (x), f_B~ (x)),

A_~ =xU: f_A~ (x)=1-f_A~(x),

Замечание:

1) A\B= A∩B,

2) AB = (A∩B)  (A∩B) ,

3) AA = U,

4) A∩ A Ø.

Пример 2:

Подмножество М всех натуральных нечетных чисел, описываемое с помощью порождающей процедуры, имеет вид: M=xN: x=1+2n, nN.

В этой записи на объектном языке множество М есть множество всех чисел вида 1+2n, а порождающей процедурой для элементов М является вычисление формулы (1+2n), в которой nN является исходным объектом.

П

n

∩X_i

i=1

ример3: M=xU: 

В этом множестве X_i являются исходными объектами для построения множества М, а операция пересечения есть порождающая процедура для заданного числа nN пересекаемых исходных подмножеств X_i.

Пример 4: M=xT: A_x├ t

В этом множестве порождающей процедурой теорем t является исчисление (Т-теория, A_x -множество аксиом, ├ - символ отношения дедуктивной выводимости).

Напоминание:

Запись М={ xu: P(x)} следует читать «множество М есть совокупность элементов х, которые обладают свойством Р». Здесь предикат Р(х) как распознающая процедура означает форму высказывания х<=P, подстановка элемента множества u в которое делает ее высказыванием (т.е. указывает принадлежность или непринадлежность элемента множества u множеству М).

Наглядное представление задаваемых множеств.

Ниже рассмотрим диаграмму Венна и графики индикаторов (функций принадлежности, характеристических функций).

А) Диаграмма Венна.

Диаграмма Венна является наглядным представлением множеств и отношений (операций в частном случае) между ними.

Исходным множеством диаграммы Венна является универсальное (основное) множество u (совокупность всех объектов изучаемой области). Его обычно представляют прямоугольником:

u

Подмножества М_i в множестве u принято представлять внутренней частью

простой замкнутой кривой, полностью лежащей внутри прямоугольника u:

Дополнение подмножества М_i на диаграмме изображается множеством точек (элементов), не принадлежащих М_i:

М₁, М₂u

u

… М_i ……… u …… ……... … ……. ……………………

М_i = u\ М_i

М_iu

М_i={ x u: xM_i}

Элементы подмножеств

хМ_i

З

М₂ u

амечание:

Для нечеткого подмножества имеем: для любого хu: μ_м~(х)=1- μ_м~(х) отношения включения между двумя множествами М₁и М₂ на диаграмме имеют вид:

М₁М₂ u

(М₁\ М₂=Ø) М₁∩ М₂= М₁

М₁∩ u= М₁ М_i U u= u

(М_iu)~ x[(xM)→(x u)]

Основные алгебраические операции над подмножествами А и В на диаграмме, изображаемой следующим образом:

U

АUВ={x u:xAVxB};

Пример: A={a,b,c}, B={b,c,d}.

Имеем: АUВ={a,b,c,d}.

Замечание:

Для нечетких подмножеств x u: xA или xB=>xA_~ U B_~

A∩B={x u: xAΛ xB}

Пример: A={a,b,c}, B={b,c,d}.

Имеем: A∩B={b,c}.

В случае A∩B=Ø, диаграмма Венна имеет вид:

U

U

Замечание:

Для нечетких подмножеств А_~ и В_~ V x u: μ_A∩B(x)=min(μ_A(x), μ_B(x)).

U

A\B={ x u: xAΛ xB}

Пример: A={a,b,c}, D={b,c,d,e}

Имеем: A\B={a}

HO: B\A={d,e}, т.е. A\B≠ B\A и (B\A) \С≠ B\(A \С).

U

AB=x u: xАΛВ, xА, xВ}={ x u: x((AUB)\(A∩B))

Пример: A={a,b,c}, B={b.c,d}. Имеем: AB=a, d}.

(х не принадлежит области пересечения)

Примечание:

1.Выше приведенные диаграммы Венна для четких подмножеств и операций позволяют наглядно пояснить свойства бинарных алгебраических операций.

Так записьAUB= ВUА означает коммутативность операции U. Аналогично, A∩B = В∩А.

AU(BUС)=(AUB)UС ассоциативность

A∩(B∩С)=(A∩B)∩С операций U и ∩.

AU(B∩С)=(AUB)∩(AUС) – дистрибутивность Uотносительно ∩.

A∩(BUС)=(A∩B)U(A∩С) – дистрибутивность ∩ относительно U.

2. Из диаграммы Венна можно установить, что:

AUØ=А; A∩u=А A∩BA

AUА= u; A∩А=Ø A∩BB

AUА=А; A∩А=А AAUB

AUu=u; A∩Ø= Ø BAUB

Если A\B= Ø, то AB (A\B)U(A∩B)=A A=B  AB и BA

3. Из диаграмм Венна видно, что одни алгебраические операции над подмножествами можно выразить через другие алгебраические операции.

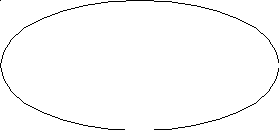
4. Диаграмма Венна для нечетких подмножеств можно представить как «размытые» замкнутые кривые. Пример: А_~={<0,1>,<1,9/10>,<2,7/10>,<3,1/2>,<4,5/17>,<5,5/101>,<6,0>}. Имеем:

u

9/10 7/20 1/2 5/17 5/101

Здесь u={0,1,2,3,4,5,6}, а характеристическая функция μ_A~(х):u→{1,9/10,7/20,1/2,5/17,5/101,0}

Б) Индикаторы.

Ниже приведем наглядное представление простейших отношений и операций с нечеткими подмножествами данного множества, используя индикаторы:

0, if xА,

μ_A~(х): А→{0,1} или μ_A~(х)=

[0,1], if xA.

Напоминание: Четкое подмножество, как и частный случай нечеткого подмножества данного множества, задается характеристической функцией вида:

0, if xА,

μ_A(х): А→{0,1}или μ_A(х)=

1, if xA.

Рассмотрим прямоугольную систему координат, на оси ординат откладываются значения μ_A~(х), а на оси абсцисс в произвольном порядке расположены элементы u. Пример:

На этой характеристике степень принадлежности каждого элемента нечеткому подмножеству изображена ординатой, а заштрихованная часть наглядно изображает нечеткое подмножество А_~ и все нечеткие подмножества, содержащиеся в А_~, т.е. А_~u. Такое представление позволяет сделать зримым простые отношения и операции на нечетких множествах ^– , U, ∩, \,.

μ_A(х) A_~

x u

Данным способом можно представить отношения включения нечеткого подмножества данного множества, операции дополнения, объединенияU и пересечения ∩, а с учетом того факта, что

А_~\ B_~= А_~∩B_~ и А_~B_~= (А_~∩ B_~)U( А_~∩B_~) можно визуально представить операции разности двух нечетких множеств данного множества и дизъюнктивной их суммы.

Замечание:

1) для подмножеств А_~ U А_~≠ u;

2) соответствующие пары символов Ø и u, U и ∩, называются двойственными символами;

3) для пустого множества Ø индикатор такой, что x u: μ_Ø(х)=0;

4) для универсума u индикатор такой, что x u: μ_u(х)=1.

Очевидно, что предикатное представление позволяет сделать зримыми теоретико-множественные отношения , = и операцииU, ∩, /, - ,  как на четких, так и на нечетких подмножествах заданного множества.

Пример1:

Пусть M = {a, b, c, d, e, f}, M₁ = {a, c, e, f}, M₂ = {a, b, c}, M₃ = {a, c}. Т.к. M₁M и M₂M, то

M₁= {<a,1>, <b,0>,<c,1>, <d,0>, <e,1>,<f,1>}

M₂= {<a,1>, <b,1>,<c,1>, <d,0>, <e,0>,<f,0>}

M₁ U M₂ = {<a,1>, <b,1>,<c,1>, <d,0>, <e,1>,<f,1>}

M₁ ∩ M₂ = {<a,1>, <b,0>,<c,1>, <d,0>, <e,0>,<f,0>}

M₁= {<a,0>, <b,1>,<c,0>, <d,1>, <e,0>,<f,0>}

А т.к. M₃M₁ и M₃M₂ , то

M₃ = {<a,1>, <b,0>,<c,1>, <d,0>, <e,0>,<f,0>}

M₁ U M₃= {<a,1>, <b,0>,<c,1>, <d,0>, <e,1>,<f,1>} = M₁

M₂ U M₃= {<a,1>, <b,1>,<c,1>, <d,0>, <e,0>,<f,0>} = M₂

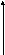
F(M₁) F(M₂) F(M₃)

1 1 1

a b c d e f

a b c d e f

a b c d e f

0 M 0 M 0 M

F(M₁ U M₂) F(M₁ ∩ M₂)

1 1

a b c d e f

a b c d e f

0 M 0 M

Пример2:

Пусть М = {a, b, c, d, e, f}

M_1~ = {<a,5/6>, <b,0>, <c, 1/2>, <d,0>, <e, 9/10>, <f , 99/100>} M

M_2~ = {<a,1>, <b,5/7>, <c, 1/3>, <d,0>, <e, 0>, <f ,0>} M

В этом случае: M_1~ U M_2~ = {<a,1>, <b,5/7>, <c, 1/2>, <d,0>, <e, 9/10>, <f ,99/100>}

M_1~ ∩ M_2~ = {<a,5/6>, <b,0>, <c, 1/3>, <d,0>, <e, 0>, <f , 0>}

Графики рисуются аналогично, как и в примере 1.

Пример:

Пусть M = {a, b, c, d} = {<a,1>, <b,1>, <c,1>, <d,1>}, M_1~ = {<a,0,3>, <b,0,2>, <c,1>, <d,0>}

Очевидно, чтоM_1~ = {<a,0,7>, <b,0,8>, <c,0>, <d,1>}

Вэтом случаеM_1~ U M_1~ < > 

M_1~ ∩ M_1~ < > 

Действительно:

M_1~ U M_1~ = {<a; 0,7>, <b; 0,8>, <c, 1>, <d, 1>} M

M_1~ ∩ M_1~ = {<a; 0,3>, <b; 0,2>, <c; 0>, <d; 0>}M

Примечание

1) С учетом того факта, что А_~\В_~ = А_~ ∩ В_~ и А_~ В_~ = (А_~∩В_~) U (А_~∩В_~) можно визуально представить операции разности и дизъюнктивной суммы двух нечетких подмножеств данного универсума.

2) Принято пары символов <, U>, <∩, U> называть двойственными (дуальными) символами.

3) Для универсума U его индикатор такой, что x  U: f_u (x) =1. Исходя из изложенного, отметим:

• Каждое бесконечное подмножество счетного множества счетно;

• Объединение счетного множества счетных подмножеств есть счетное множество, т.е.: , где |М_I| = |N|.

• Каждое бесконечное множество содержит в качестве подмножества множество мощности χ₀, что означает существование кардинальных чисел, не являющихся натуральными.

• Не существует множества наибольшей мощности (так же, как нет наибольшего натурального числа)

• Д

  |M|

  2

  2

  ля любого бесконечного множества первая мощность, превосходящая мощность этого множества, есть мощность множества всех его подмножеств (это теорема

Г. Кантора |M|<|B(M)|=2^|M|). В частности, никакие два из множеств |M|, 2^|M| , ….

M=N получается бесконечно много различных кардинальных чисел.

Любое кардинальное число α можно отождествить с наименьшим порядковым числом мощности α. В частности, х₀ соответствует порядковому числу ω₀, х₁ – ординалу ω₁ и т.д. Таким образом, шкала ординальных чисел является подшкалой шкалы порядковых (трансфинитных, ординальных) чисел.

В) Понятие о трансфинитных числах.

Трансфинитное (ординальное) число (ординал), как обобщение понятия порядкового числа на бесконечные упорядоченные множества, есть порядковый тип вполне упорядоченного множества.

Примеры:

1) Для М = {x₁ , x₂ , … , x_n} на котором задан порядок =, порядковое число записывается так: Ord M = |{1 , 2 , 3 , … , n} |= n = Card M;

2) Наименьшее бесконечное ординальное число ω есть Ord N = ω;

3) Для <Q, ≤ > и <Д, ≤ > ординалы обозначают символами {, λ }, т.е. Ord Q =  Ord Д = λ;

4) Множество, состоящее из числа 1 и чисел вида , упорядоченных отношением, имеет порядковый тип ω+1 , т.е.

Ord{ и ,nN} = ω+1

В приведенных примерах множества являются линейно-упорядоченными (т.е. реляционными системами вида ) с первым элементом.

Так, числа натурального ряда N, расположенные в порядке возрастания, образуют линейно-упорядоченное множество<N, ≤ >, первым элементом которого является число 1. Однако, линейно-упорядоченное множество <N, ≥ > не имеет первого элемента.

В случае, когда все непустые подмножества линейно-упорядоченного множества имеют первый элемент, говорят о вполне упорядоченном множестве.

Пример: Все числа натурального ряда N, расположенные в порядке убывания, т.е. когда <N,≥>, образуют линейно-упорядоченное, но не вполне упорядоченное множество (в этом случае ни одно бесконечное подмножество не имеет первого элемента). Итак, множество М с заданным бинарным отношением порядка и удовлетворяющее условиям:

1. либо x<y, либо y<x;

2. x≤x (рефлексивность);

3.(антисимметричность);

4.(транзитивность).

5. В любом непустом подмножестве М_iМ существует такой элементa , что ax для всех xМ_i есть вполне упорядоченное множество.

Два упорядоченных множества А и В называются подобными (или имеют один и тот же порядковый тип), если между их элементами можно установить взаимо-однозначное соответствие, сохраняющее порядок элементов (т.е. <A, ≤ > и <B, ≤ > - изоморфные реляционные системы). Очевидно, что все конечные вполне упорядоченные равномощные множества подобны между собой.

Пример:

Упорядоченные множества А={a₁, a₂, a₃} и B={b₁, b₂, b₃} подобны между собой, <A, < > и <B, < > имеют вид:

A Г_f = Г_f ^‘ B

|A| = |B|OrdA = OrdB

Очевидно, что:

1) не существует множества всех порядковых чисел (также как не существует и наибольшего ординала);

2) вполне упорядоченным бесконечным множеством различной мощности соответствуют различные трансфинитные числа (ординалы);

3) в отличие от конечных множеств , бесконечные вполне упорядоченные множества могут быть равномощными , не будучи подобными (т.е. определяемые различными ординалами).

Пример.

Для вполне упорядоченного множества <N, ≤ > трансфинитным числом является число ω , т.е.

Ord N = ω , а для упорядоченного множества <М, ≤ >, где CardM = |{xZ: x=1 и }| =x_0, где nN, трансфинитным числом будет ω+1 , т.е. Ord {xZ⁺: x=1 и } = ω+1.

Основы комбинаторного анализа.

Комбинаторный анализ (комбинаторика) – раздел дискретной математики , объектом изучения которого являются задачи выбора и расположения элементов заданного множества по тем или иным заданным правилам.

Каждое порядковое число α можно представить в виде α=ℓ+n, где ℓ - предельное порядковое число (т.е. число, не имеющее предшественников), nN, а сумма понимается как сложение порядковых типов.

Рассмотрим несколько ее классических задач.

Задача 1.

Дано:

|M|=n, |Y|=m. Сколько существует функциональных отображений Г_ф: MY ?

Решение:

Множество функциональных отображений элементов множества М во множество элементов Y есть множество кортежей вида:

{

n

П({x_i}×y)

i=1

<x₁,Г_f(x₁₎>,…,< x_n, Г_f(x_n) >} , где x₁ , x₂ , … , x_nM; Г_f(x₁₎,…,Г_f(x_n) Y; |{ Г_f(x₁₎,…,Г_f(x_n)}| ≤ m.

Поскольку эти кортежи длины n являются элементами полного произведения ,

то имеем {<x₁, y₁>, <x₁, y₂>,...<x₁,y_m>}{<x₂, y₁>, <x₂, y₂>,...<x₂,y_m>}... {<x_n,y₁>, <x_n,y₂>,...<x_n,y_m>}. Из того, что |{<x_i,y₁>,<x_i,y₂>,...,<x_i,y_m>}| = m, а число таких сомножителей n(i=1,n), помечаем, что мощность множества всех функциональных отображений Г_f: M→Y равна mⁿ (т.е. |Y|^|M|).

Замечание.

1) Полученная формула может рассматриваться как формула элементарной комбинаторики для числа размещений из m по n с повторениями элементов М, т.е. P₁(m,n)=mⁿ. В этом случае элементы множества М называются частицами (шарами!), элементы Y – ячейками (урнами!), а Г_f определяет заполнение различных ячеек различными частицами.

2) Традиционной интерпретацией P₁(m,n) является способ окраски элементов множества М (Y трактуется как множество «красок», а Г_f(x)Y - как цвет окраски элемента xM).

Примеры.

• Из символов алфавита мощностью 32 можно составить пятибуквенные слова (цепочки, векторы, кортежи) 32⁵ способами.

• Окрасить полы в 3-х комнатах пятью цветами возможно 125 вариантами (5³).

• Мощность множества всех четких подмножеств данного множества B(м) (булеан) равна . (В этом случае говорим об индикатореM_i). Действительно, каждое собственное подмножество M_i и несобственные подмножества Ф и М исходного множества М можно задать своей характеристической функцией (индикатором). Очевидно, что для |M| = n таких характеристических функций 2ⁿ , т.к. в Ø : M  Y |Y|=2. Поэтому |B(M)| = 2^|M| .

• Мощность множества всех нечетких подмножеств данного множества B_~(м) равна k^|M| , где k – число степеней принадлежности элемента x нечетному подмножеству, |B_~(м)|=k^|M|. Действительно, в этом случае индикатор каждого нечеткого подмножества можно найти из

Г_ф: MY , когда |Y| = к (очевидно |B(м)| < |B_~(м)|).

Задача2.

Для |М|=n и |Y|=m определить функциональное отображение Г_ф: MY такое, что

|{Г_ф(х1), Г_ф(х2),…, Г_ф(хn)}|=m, .

Решение.

В данной постановке задача интерпретируется как размещение частиц в ячейках без повторений.

Элемент y₁ множества можно выбрать m способами, элемент y₂ – m-1 способами, и т.д. Это дает m(m – 1)...(m – n + 1) возможностей выбора последовательностей .

Итак, число размещений из m по n без повторений равно: .

Примеры.

1. Из трех цифр 1,2,3 можно построить девять двузначных чисел: 11,12,13,21,22,23,31,32,33

(исходя из Ф₁(3,2)=3²), среди которых шесть двузначных чисел не имеют повторения исходных цифр: 12,13,21,23,31,32. (исходя из ).

2) Десять микросхем можно разместить на плате с десятью позициями для них по горизонтали 10! = 3628800 способами (исходя из Ф₂ (10,10) = 10!).

Замечание. Ф(m,m) часто называют перестановкой.

Задача 3.

Определить число всех k-элементарных подмножеств n-элементного множества M.

Решение.

Поставленная задача решается с привлечением сочетания из n по k:

Пример. Для множества, состоящего из 3-х элементов, M={a,b,c} определить число подмножеств, состоящих из 1-го элемента, 2-х и 3-х элементов и не содержащих ни одного элемента.

Имеем ;;;.

Очевидно, что |B(м)| = =8 и .

Замечание.

1) Сочетания являются биномиальными коэффициентами бинома Ньютона: .

2) Принимая в биноме Ньютона x=1 , имеем: .

Отсюда следует, что мощность множества всех подмножеств заданного множества равна 2ⁿ, т.е.

|B(м)| = , где |M|=n.

3) Для сочетаний имеют место зависимости:

Последнее тождество тесно связанно с треугольником Паскаля для нахождения :

Задача 4.

2

3 3

4 6 4

5 10 10 5

Определить число разбиений n-элементного множества M на k блоков.

Решение.

Поскольку разбиение множества М на подмножества должно удовлетворять уравнениям иØ, , что задача решается с привлечением чисел Стирлинга 2-го рода (здесь- множество всех разбиений множества М наk блоков).

Числа Стирлинга можно определить через следующие соответствия:

;

для k>n;

для 0<k<n;

для n0;

для n>0;

;

Пример. .

Действительно: .

Этим расчетом мы решили задачу подсчета числа разбиений множества |М| = 4 на два блока.

Задача перечисления сводится к нахождению блоков разбиения. Имеем:

; ;;;;;.

Замечание. Формально число Стирлинга 2-го рода определяется выражением:

.

Задача 5.

Определить множество всех различных разбиений n-элементного множества М.

Решение.

Число всех разбиений n-элементного множества М есть число Белла

Так, если n=4, то .

Задача 6.

Определить мощность множества, заданного своим подмножествами.

Решение.

Подобные задачи решаются с привлечением принципа включения-исключения.

Очевидно, что |AUB| = |A| + |B| - |A∩B|. Это видно из диаграммы:

|A U B U C| = |A| + |B| + |C| - |A∩B| - |B∩C| - |A∩C| + |A∩B∩C|.

Ив общем случае:

.

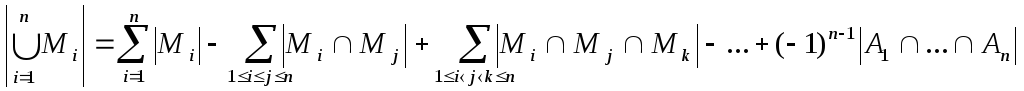
Замечание.

Если множество М задано n блоками разбиения (а не как в общем случае – блоками покрытия), что - это так называемое обобщенное правило суммы.

Аксиоматики теории множеств.

Ι. Аксиоматика содержательно построенных множеств.

а) Канторовская («наивная», классическая) теория множеств, базирующаяся на интуитивных аксиомах, является противоречивой содержательной теорией конечных и актуально-бесконечных четких подмножеств данного множества.

Противоречивость этой теории обусловлена, прежде всего, агрегатной точкой зрения и интуитивными принципами, лежащими в понимании актуальной бесконечности.

Интуитивные принципы объемности (экситенциональности) и абстракции (свертывания) сформулированы Кантором в виде:

• Множества А и В считаются равными, если они состоят из одних и тех же элементов.

• Для любого свойства P(x) существует множество М всех элементов x, обладающих этим свойством.

Именно принцип абстракции делает Канторовскую теорию противоречивой (парадоксальной). Отказ от этого принципа исключает возможность появления в «наивной» теории множеств известных парадоксов Рассела и Кантора.

В соответствии с традиционными логическими представлениями парадокс Рассела формализуется следующим образом:

(xM) ~ ך (xx) (1); где М – множество всех множеств, не являющихся элементами самих себя;

ך, ~ - соответственно операторы отрицания и эквивалентности.

Символ М является термином конкретного множества и, следовательно, входит в область значений переменной x. Поэтому из (1) получаем противоречивое следствие:

(ММ) ~ ך(ММ) (2).

Это антиномия (парадокс) показывает, что в классической теории множеств с «множеством всех множеств» работать нельзя.

Парадокс Кантора является следствием применения к «множеству всех множеств U» понятия булеан В(U). Итак, имеем следующее противоречие: В(U)U , но |В(U)|>|U|. Эта антиномия доказывает не существование множества всех множеств.

Замечание.

Если парадокс Кантора возникает для бесконечных множеств, содержащих себя в качестве своего элемента, то парадокс Рассела связан с множествами, не содержащими себя в качестве своих элементов.

б) В рамках атрибутивного подхода к понятию множества теорема Кантора: |В(U)|=2^|U| не имеет места, но сохраняется и получает чисто логическую интерпретацию, все основные теоретико-множественные понятия. При этом парадокс Рассела получает простое объяснение: символ x в (1) является переменной для объектов, в то время как М – одноместный предикат, обозначающий определенное свойство; следовательно, не входит в область значений переменной x, а поэтому переход от (1) к (2) недопустим.

Именно в рамках атрибутивной точки зрения на множество содержательная теория множеств становится непротиворечивой.