Основные понятия содержательной теории множеств.

Производные понятия

Исходные понятия

Алгебраические системы

Соответствия и

морфизмы

множество

отношения

инцидентности

элементтыт

Подмножества данного множества

Операции

Алгебраические

Не алгебраические

четкие

нечеткие

Основные производные понятия содержательных теории множеств.

Определение1.

Множество А, каждый элемент которого является элементом другого множества М, называется подмножеством данного множества М.

Символическая запись А  М (здесь  - символ отношения включения всех элементов А в М, А является несобственным подмножеством М) и АМ (А – собственное подмножество М).

Графической интерпретацией отношения включения между множеством может быть

Диаграмма Вена:

собственное подмножество несобственное подмножество

U

U

Пример1:

M={a,b,c}. Подмножеств 8: собственных 6 ({a},{b},{c},{a,b},{b,c},{a,c}), несобственных 2 ({a,b,c},)

Т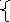ак же для заданного множества все его подмножества могут быть представлены с помощью характеристической функции (индикатора):

F(x)= 0, если хМ; (или условно: f_A(х):М0,1)

1,если х М.

Пример2:

Дано: М={a,b,c}. Представить все его подмножества с помощью индикатора.

Решение:F(x)= 1, если хМ → хА;

0,если х М → х А.

1)М={<a,1>,<b,1>,<c,1>} – индикатор для множества М;

2)А₁={<a,1>,<b,1>,<c,0>} – индикатор для множества А₁ , {a,b}

3)A₂={<a,1>,<b,0>,<c,1>} – {a,c}

4)A₃={<a,0>,<b,1>,<c,1>} − {b,c}

5)A₄={<a,1>,<b,0>,<c,0>} – {a}

6)A₅={<a,0>,<b,1>,<c,0>} – {b}

7)A₆={<a,0>,<b,0>,<c,1>} − {c}

8)A₇={<a,1>,<b,1>,<c,1>} – {a,b,c}

9)A₈={<a,0>,<b,0>,<c,0>} – 

Пояснения:

1. Кортеж – это конечная последовательность, допускающая повторяющиеся элементы данного множества (или данных множеств), обозначается: <a1,a2,a3...an>.(см. опр.2 ниже)

2) В этих выражениях (1-9) множество есть множество кортежей (спаренных векторов), первой компонентой которых являются элементы множества M, а второй компонентой – единица/ноль (т.е. принадлежность/непринадлежность элемента множества M множеству A).

3) Говорят что индикатор f_A(х) множества А, определенный на множестве М, задает четкое подмножество А множества М.

4) Если степень принадлежности элемента множестваM множеству A_~ есть субъективно множественная оценка F_A~(x)= 0, если хА,

[1,0],если хА;

то говорят о нечетком подмножестве A_~ множества М (множество М всегда четко!), и записывают A_~  М.

Логическая экспликация (разъяснение) понятия подмножества А множества М с агрегатной и атрибутивной точек зрения следующие:

х(() (1)

( (2)

где метасимволы  и следует считать соответственно как “эквивалентность” и “если…то”.

Примеры:

а) Множество красавиц МГИЭМа, есть нечеткое подмножество A_~ всех студенток МГИЭМ M, т.е. A_~ М (это очевидно потому, что понятие “красавица” для каждого человека субъективно и, следовательно, степени оценки красоты той или иной студентки различны для различных людей).

б) Пусть M={0,1,2,3,4,5,6,7,8,9}. Привести подмножество ”большие цифры”. Возможный вариант (субъективный):

A={<0,0>,<1,0>,<2,1/1000>,<3,1/100>,<4,1/10>,<5,0.5>,<6,0.6>,<7,0.7>,<8,0.9>,<9,1>}. Здесь первая компонента каждого кортежа есть цифра множества M, а вторая компонента этих же кортежей есть степень оценки принадлежности цифры к искомому подмножеству.

Определение2. Конечная последовательность, допускающая повторения элементов данного множества (или данных множеств), называется кортежом (n-кой, вектором, набором, упорядоченным множеством).

Условно кортеж записывают последовательностью элементов заданного множества в угловых скобках (пусть А={a,b,c}, тогда: < a,a,b> - кортеж длины 3 или тройка, <a,b> - пара).

Примеры:

1.Слово в алфавите A есть кортеж.

2.Команда в программе для ЭВМ есть последовательность символов из алфавита языка программирования.

3.Алфавит русского языка есть кортеж длины 32.

4.Программа для ЭВМ есть кортеж кортежей.

5.Координаты точки в n-мерном пространстве образуют кортеж.

Пояснения:

1.В условной записи кортежа элементы, его образующие, называются компонентами (координатами).

2.Число компонент кортежа называется его длиной. Так, принято кортеж длиной два <a₁,a₂> называть парой (или упорядоченной парой), кортеж длины три <x₁,x₂,x₃> - тройкой

3.Кортеж длины n можно интерпретировать как n-мерный вектор, или как точку в n-мерном пространстве, а каждую компоненты кортежа можно рассматривать в этом случае как проекции вектора на соответствующие оси.

Определение3. Декартовым (прямым) произведением множеств M_i(i=1…n) называется множество, элементами которого являются кортежи длиной n такие, что каждая

j-ая компонента есть элемент множества M_j.

П_i=1.._nМ_i =М₁ * М₂ * …*М_n = {<x₁,x₂,...,x_n>: x_jM_j, j=1..n}

Замечание:

В том случае, если M₁=M₂=…=M_n =М, то говорим об универсальном полном отношении и записываем: Мⁿ (M², M³ и т.д.)

Пример 1. Сколько вариантов окраски квадрантов круга возможно, если допускается пять цветов краски.

Решение: Поставленная задача всех вариантов окраски круга решается с привлечением математического понятия универсального отношения Mⁿ.

, , ,…………,

Очевидно, что кортеж длины 4, каждая компонента которого есть цвет краски, есть элемент декартового произведения. Пусть цвета краски образуют множество M = {к, б, з, с, ф}. Тогда М⁴ = М  М  М  М и М⁴ = 5⁴ = 625 (здесь условная запись |Mⁿ| означает число картежей длины 4).

Пример 2. Всё множество координат всех клеток шахматной доски можно записать декартовым произведением вида {a,b,c,d,e,f,g,h}  {1,2,3,4,5,6,7,8} = {<a,1>, …, <a,8>, <b,1>, …, <b,8>, …, <h,8>}. M₁={a,b,c,d,e,f,g,h}, M₂={1,2,3,4,5,6,7,8}, имеем число всех пар, т.е. |M₁M₂|, равным 64.

Определение 4. Подмножество S декартового произведения П_i=1.._nМ_i называется n-арным соответствиeм элементов множеств M_i.

Формально S  П_i=1.._nМ_i.

Частные случаи.

1. Если n=2, то говорят о бинарном соответствии S  M₁  M₂ и пишут: q=<M₁,M₂,S>

2. Если говорят о подмножестве кортежей универсального отношения Mⁿ, то имеют в виду n-арное отношение R, т.е. R  Mⁿ.

3. R  M² называют бинарным отношением на множестве M ( пишут: q=<M,R₂>).

4. Однозначное n-арное отношение есть n-местная функция

Пример функции:

р

В этом случае R_f P² является функциональным (однозначным) бинарным отношением на множестве Р

p

Пример не являющийся функцией:

p

Это функциональное соответствие элементов двух множеств, т.е. S_f P×T

t

Пример. Пусть M = {х₁,х₂,х₃} и R ={<x₁, x₁>,< x₂, x₁>,< x₃, x₁>}.

Рассматривая множество первых координат кортежей отношения, как его область определения, а множество вторых координат, как область значений бинарного отношения, представим функцию как частный случай соответствия элементов множества М.

М R_f M

Замечание. Поскольку S является подмножеством, то можно говорить о нечётких соответствиях, отношениях, функциях.

Определение 5. Алгебраической n-арной (n-местной) операцией на множестве M называется n-местная функция у = f(x₁,x₂,…,x_n), у которой область определения аргументов x_i и область значений функции совпадают (n  N).

Формальная запись f: MⁿM означает, что алгебраическая операция функциональна (однозначна) и замкнута.

Пояснение.

1. Тот факт, что алгебраическая операция является частным случаем бинарного однозначного соответствия (отражается в её формальной записи f: Mⁿ  M.), можно пояснить графически:

М_n M_n

R_f

Очевидно, что алгебраическая операция может быть не всюду определенной, т.е. быть частичной, на множестве элементов М, а также может быть и нечеткой.

1. Поскольку алгебраическая операция по n элементам множества M определяет (n+1) элемент этого же множества M, то n-местную алгебраическую операцию можно рассматривать и как (n+1)-арное однозначное отношение на множестве M.

2. Если f: M  M, то говорят об унарной (одноместной) алгебраической операции; f: M²  M, то имеют в виду бинарную (двухместную) алгебраическую операцию.

Определение6. Алгебраической системой A называется кортеж <M,O,R>, первая компонента которой M есть непустое множество, вторая компонента O – множество алгебраической операций, третья компонента R – множество отношений на множестве M.

Пояснение.

1. Множество M алгебраической системы A называют несущим, или основным множеством.

2. Совокупность алгебраических операций и отношений алгебраической системы называют сигнатурой . В этом случае алгебраическая система записывается парой <M, >.

3. Алгебраическая система <M,O> называется универсальной алгеброй (или просто алгеброй), если на основном множестве M множество отношений R пусто (т.е. R = ).

4. Алгебраическая система A = <M,R> называется реляционной системой (или моделью), если на основном множестве M заданы только отношения R (т.е. в этом случае пусто множество операций O, что означает O = )

Приведем в систему все множество символов, используемых в читаемом курсе.

Алфавит языка теории множеств.

А=А₁А₂А₃А₄

Основные символы

А₁А₂А₃

Вспомогательные (разделительные) символы

Символы

операций А₂

индивидуальные

общие

Знаки препинания

скобки

точка

двоеточие

круглые ( )

фигурные {}

прямые | |

угловые < >

Символы соответствий А₃

Символы объектов А₁

Индивидуальные

(собственные) символы соответствий

Общие символы соответствий

Индивидуальные (именные) символы объектов

Общие символы

объектов

Индивидуальные символы функций

индивидуальные символы отображений

индивидуальные символы отношений

функций

отображений

отношений

множеств

множеств

элементов множеств

элементов множеств

1. Общие символы множеств и элементов множеств.

Общим обозначением множеств и элементов множеств соответственно являются заглавные и строчные буквы любого алфавита естественного языка (часто с индексами для одного символа).

Пример:

а) x,y,z – элементы множества М, т.е. M={x,y,z};

б) х₁, х₂, х₃ – элементы множества Х, т.е. X={ х₁, х₂, х₃}.

2. Индивидуальные символы множеств:

Z – множество целых чисел;

N – множество натуральных чисел;

Q – множество рациональных;

D - множество действительных чисел.

В(М) – булево множество (множество всех подмножеств данного множества М).

П(М) – множество разбиений множества М.

U – универсальное множество (множество, содержащее в качестве своих подмножеств любое множество).

Ø – пустое множество (часто записывают и так: {}, |M|=0 ).

3. Индивидуальные символы элементов множеств.

Примем за имена конкретных элементов натуральные числа nN.

Примером далее изучаемых структурированных множеств является алгебраическая система <M, , ,  > (где O = {, } – множество из операции объединения  и операции дополнения , а R = {} – множество, состоящее из отношения включения ).

Алгебра Кантора (алгебра множеств) <B(M), , >, (несущим множеством которой является булеан B(М) (т.е. множество всех подмножеств данного множества М), а множеством операций

O= {, , } - булевы операции объединения , пересечения  и дополнения ), алгебра логики.

Примерами реляционной системы является: метрическое пространство <M,P>, (где P – метрика), языки науки - <A,S₁>, < A,S₁,S₂> ( здесь А - множество символов алфавита, S₁,S₂ –соответственно, отношения синтаксиса и семантики).

Примером <M,R> является так называемое дискретное множество, т.е. множество (оно всегда дискретно!), на котором задано расстояние, причем любое из них не меньше некоторой величины ε.

Символический язык содержательных теорий множеств.

В процессе изучения курса будем различать объектный язык теории множеств и метаязык, средствами которого изучается объектный язык. Под языком теории множеств будем понимать реляционную систему L=<A,R>=< A,S₁,S₂>, основным множеством которой являются символы алфавита A, а отношения синтаксиса позволяют получать синтаксически правильные языковые выражения, среди которых выделяют формулы F.

В этом плане L = <A,R>, B  A  A²  … Aⁿ, F B.

Определение7. Алфавитом языка A теории множеств называют множество непересекающихся подмножеств символов объектов A₁, операций A₂, правил сопоставления A₃, и разделительных знаков A_4.

Формально A = A₁  A₂  A₃  A₄

A₁  A₂ = , A₁  A₃ = , A₁  A₄ = , A₂  A₃ = , A₂  A₄ = , A₃  A₄ =  (в этом случае говорят, что множество A разбито на подмножества). Графически это может быть представлено так:

Синтаксис языка L часто описывают формальной грамматикой. В этом случае формальная порождающая грамматика- кортеж, состоящий из множества терминальных Т (основных) символов, нетерминальных N символов, начального символа J и множества продукций P, т.е.

J =<T, H, J, P>, где J - грамматика

TH=A, TH=, Jначальный символ (это нетерминальный символ)

Символический язык теории множеств может быть записан с помощью порождающей грамматики:

<T={X,Y,Z,…. ,Z_x, , , , , , , , , , ,  },

H={J,K}, J, P={J(JJ), J(JJ), J(J), J(JJ), J(JJ), J(JJ), J(JJ), J(JJ), J(JJ)

Этот язык теории множеств как множество формул F основные символы этой формальной порождающей процедуры (основные символы- обозначения множеств),