
- •Глава 4. Вычислительная математика.
- •Рекомендуемая литература
- •Дополнительная
- •Методология решения задач вычислительной математики
- •Исходные понятия
- •Элементарная теория погрешностей
- •Оценка погрешности
- •2.Метод Лагранжа.
- •3.Метод Ньютона.
- •0 X
- •I. Метод проб
- •II.Метод хорд
- •III.Метод Ньютона (метод касательных)
- •Комбинированный метод хорд и касательных
Комбинированный метод хорд и касательных
Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее.
Пусть
дано уравнение
![]() ,
корень
,
корень![]() отделен и находится на отрезке
отделен и находится на отрезке![]() .
Применим комбинированный метод хорд и
касательных с учетом типа графика
функции.
.
Применим комбинированный метод хорд и
касательных с учетом типа графика
функции.
Если
![]() ,
то метод хорд дает приближение корня с
недостатком, а метод касательных – с
избытком:
,
то метод хорд дает приближение корня с
недостатком, а метод касательных – с
избытком:
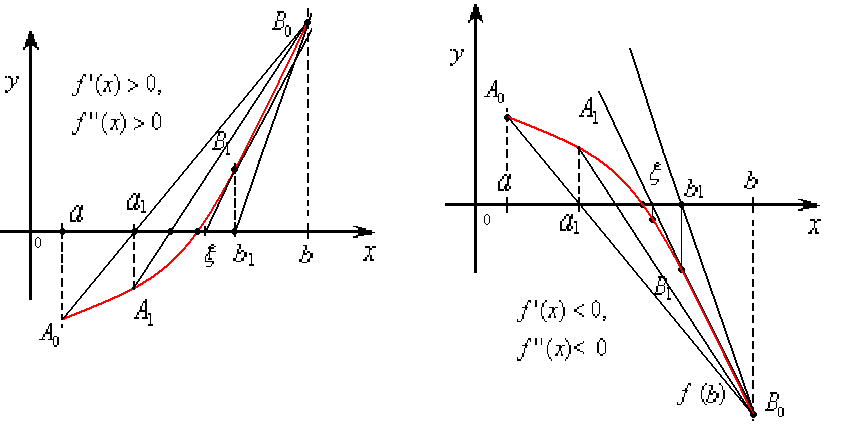
Если
же
![]() ,
то методом хорд получаем значение корня
ч избытком, а методом касательных – с
недостатком:
,
то методом хорд получаем значение корня
ч избытком, а методом касательных – с
недостатком:
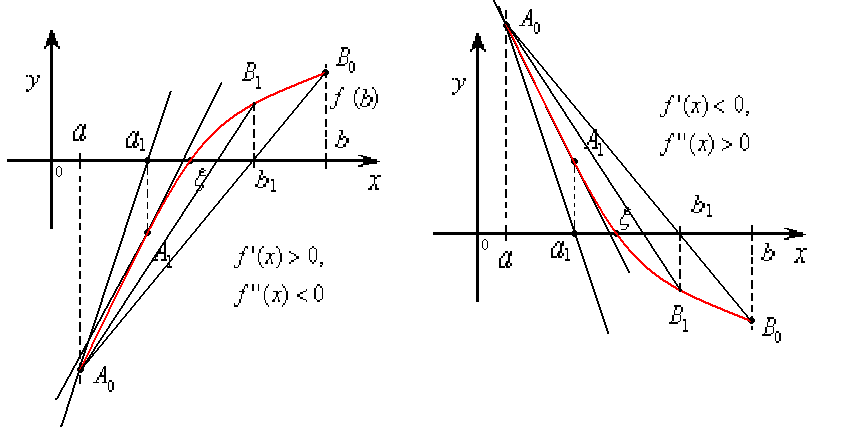
Однако,
во всех случаях искомый корень
![]() заключен между приближенными корнями,
получающимися по методу хорд и по методу
касательных, т.е. выполняется неравенство:
заключен между приближенными корнями,
получающимися по методу хорд и по методу
касательных, т.е. выполняется неравенство:![]() ,
где
,
где![]() -
приближенное значение корня с недостатком,
-
приближенное значение корня с недостатком,![]() - с избытком.
- с избытком.
Вычисления следует вести в таком порядке:
-если
![]() ,
то со стороны концаa
лежат
приближенные значения корня, полученные
по методу хорд, а со стороны конца b
– значения, полученные по методу
касательных, и тогда:
,
то со стороны концаa
лежат
приближенные значения корня, полученные
по методу хорд, а со стороны конца b
– значения, полученные по методу
касательных, и тогда:
![]() ;
;![]() .
.
Поскоку
теперь искомый корень
![]() находится на отрезке
находится на отрезке![]() ,
то, применяя к этому интервалу
комбинированный метод, получаем:
,
то, применяя к этому интервалу
комбинированный метод, получаем:![]() ;
;![]() и вообще:
и вообще:![]() ;
;![]() .
.
-если
же![]() ,
то со стороны концаa
лежат
приближенные значения корня, полученные
по методу касательных, а со стороны
конца b
– значения, полученные по методу хорд,
и тогда:
,
то со стороны концаa
лежат
приближенные значения корня, полученные
по методу касательных, а со стороны
конца b
– значения, полученные по методу хорд,
и тогда:
![]() ;
;![]() .
.
Комбинированный
метод очень удобен при оценке погрешности
вычислений. Процесс вычислений
прекращается, как только станет
выполняться неравенство:
![]() .
.
За
приближенное значение корня следует
принять
![]() ,
где
,
где![]() -
приближенное значение корня
-
приближенное значение корня![]() с недостатком,
с недостатком,![]() - с избытком.
- с избытком.
Пример
Комбинированным
методом хорд и касательных уточнить до
![]() корни уравнения
корни уравнения![]() .
.
Решение
отделим корни аналитически. Имеем:
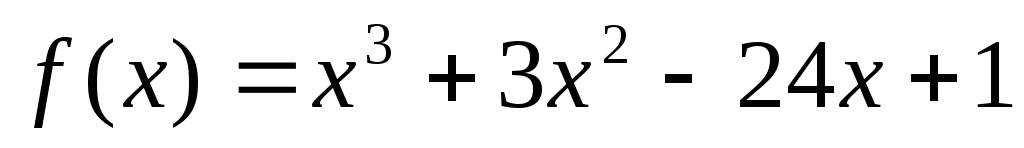 ,
,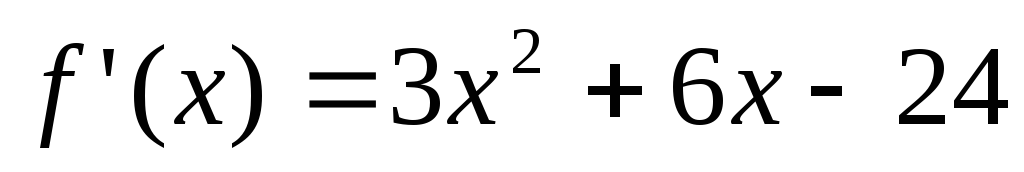 ,
т.е. корни производнойx1=-4,
x2=2.
,
т.е. корни производнойx1=-4,
x2=2.
Составим таблицу знаков функции:
|
x |
-∞ |
-4 |
2 |
+∞ |
|
sign f(x) |
- |
+ |
- |
+ |
Данное
уравнение имеет три действительных
корня:
![]() .
.
Уменьшим промежутки нахождения корней до длины, равной 1:
|
x |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
sign f(x) |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
- |
+ |
Итак,
![]() .
.
2)уточним комбинированным методом хорд и касательных корень, лежащий в интервале (-7;-6).
Имеем
f(-7)=-27<0,
f(-6)=37>0
и
![]() ,
,![]() ,
,![]() .
Это означает, что применяем формулы:
.
Это означает, что применяем формулы:![]() ;
;![]() .
Здесьa0=-7,
b0=-6.
Вычисления сведем в таблицу:
.
Здесьa0=-7,
b0=-6.
Вычисления сведем в таблицу:
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
0 |
-7 |
1 |
49 |
-343 |
-27 |
81 |
64 |
-0,333 |
-6,667 |
|
-6 |
36 |
-216 |
37 |
-0,578 |
-6,578 | ||||
|
1 |
-6,667 |
0,089 |
44,49 |
-296,34 |
-1,985 |
73,345 |
6,037 |
0,027 |
-6,640 |
|
-6,578 |
43,27 |
-284,63 |
4,052 |
-0,060 |
-6,638 | ||||
|
2 |
-6,640 |
0,02 |
|
|
|
|
|
|
|
|
-6,638 |
|
|
|
|
|
Из
таблицы следует, что
![]()
3)
Определим
![]() Имеемf(0)=1>0,
f(1)=-19<0
и
Имеемf(0)=1>0,
f(1)=-19<0
и
![]() ,
,![]() ,
,![]() .
Как и в случае нахождения
.
Как и в случае нахождения![]() (воспользовавшись теми же формулами,
но в которыхa0=0,
b0=1),
строим таблицу для уточнения искомого
корня. В результате получаем
(воспользовавшись теми же формулами,
но в которыхa0=0,
b0=1),
строим таблицу для уточнения искомого
корня. В результате получаем
![]() .
.
4)
Для уточнения приближенного корня
комбинированным методом хорд и касательных
на интервале (3;4) имеем: f(3)=-17<0,
f(4)=7>0
и
![]() ,
,![]() ,
,![]() .
.
Расчетные
формулы в этом случае следующие:
![]() ;
;![]() .
Построив таблицу последовательных
вычислений, находим, что
.
Построив таблицу последовательных
вычислений, находим, что![]() .
.
Метод итерации (метод последовательных приближений)
Пусть на отрезке [a,b] отделен вещественный корень непрерывной функции f(x).
Заменим уравнение f(x)=0 эквивалентным ему уравнением x=φ(x).
Выберем каким либо способом x0 є [a,b] и подставим его в уравнение x=φ(x); тогда имеем x1= φ(x0). Затем это значение x1 подставим снова в правую часть x=φ(x) , то получим х2= φ(x1).
Повторяя этот процесс последовательность, чисел хn= φ(xn-1),которая может сходиться (т.е. х0 , х1 , х2 , ….. , хn , … имеет предел , который и является корнем уравнения f(x)=0) или расходится (в этом случае х0 , х1 , х2 , ….. , хn , … не имеют предела).
Условия , при котором итерационный процесс сходится , формируется в теореме : если уравнение x=φ(x) на отрезке [a,b] a= φ(x)=b имеет единственный корень и во всех точках этого отрезка производная f '(x) удовлетворяет неравенству | φ' (x)|≤q<1, то итерационный процесс сходится ,а нулевое приближение х0 можно взять любое число из отрезка[a,b] .
Очевидно , что чем меньше | φ' (x)| , тем лучше сходимость итерационного процесса .
Для лучшего уяснения сути метода итерации приведем геометрические итерации a,b,c,d.
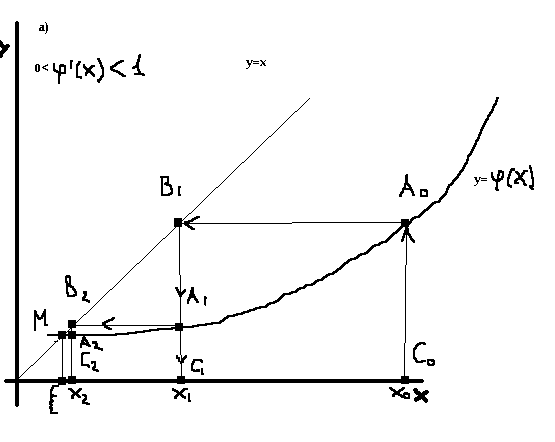 Здесь
ξ – абцисса точки пересечения функций
т.е. искомый корень f(x)=0
; х0 первое ( начальное ) приближение
корня , x0
є [a,b];
x1=φ(x0)
(т.к. А0 С0= φ(x0),
B1C1
= А0 С0= x1
), х2 = φ(x1)
, х3 = φ(x2),
…. φ(xn-1)=xn.
Здесь
ξ – абцисса точки пересечения функций
т.е. искомый корень f(x)=0
; х0 первое ( начальное ) приближение
корня , x0
є [a,b];
x1=φ(x0)
(т.к. А0 С0= φ(x0),
B1C1
= А0 С0= x1
), х2 = φ(x1)
, х3 = φ(x2),
…. φ(xn-1)=xn.
Последовательное приближение х0 , х1 , х2 , ….. , хn , … (общие абциссы точек графиков обеих функций ) монотонно убывают , что характеризует сходящийся итерационный процесс (каждая последующая приближение хn ближе к истинному корню ξ чем каждое предыдущее xn-1 ). Отметим , что в рассматриваемом случае 0< φ' (x)<1 , кривая φ(x) пересекает биссектрису у=х в точке М=(ε, φ(ε)) и при х>ξ кривая у= f(x) лежит под биссектрисой
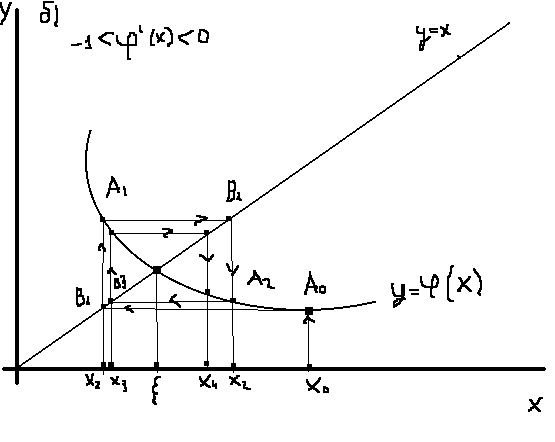 Здесь
φ' (x)<0
, но по абсолютной величине меньше 1 ,
т.е. | φ' (x)|<1.
Здесь
φ' (x)<0
, но по абсолютной величине меньше 1 ,
т.е. | φ' (x)|<1.
Итерационный процесс и в этом случае сходится , однако приближения колеблются около точного значения корня ξ. В отличие от случая «а», где ломанная линия А0 , B1 , A1 , B2 ,A2……… имеет вид лестницы, ломаная линия А0 , B1 , A1 , B2 ,A2……… случая «б» имеет вид спирали .
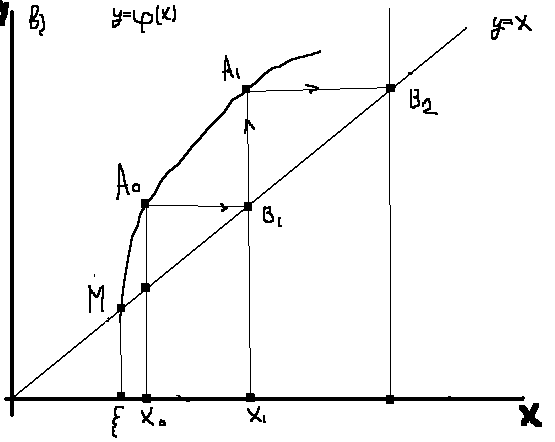
Здесь | φ' (x)|>1 , кривая у= φ(x) пересекает биссектрису у=х в точке М=(ξ, φ(ξ)) и при х>ξ лежит над биссектрисой .В таком случае итерационный процесс расходится .
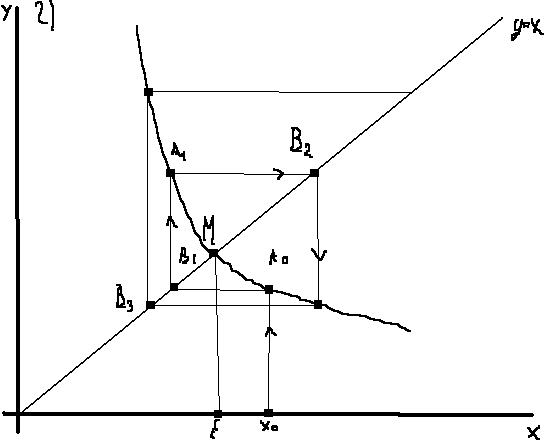 Здесь
| φ' (x)|>1.Последовательные
приближения удаляются от точного
значения корня ξ т.е. итерационный
процесс
расходится .
Здесь
| φ' (x)|>1.Последовательные
приближения удаляются от точного
значения корня ξ т.е. итерационный
процесс
расходится .
Итак , если в некоторой окрестности [a,b] корня ξ уравнение х=φ(x) производная φ' (x) сохраняет постоянный знак выполняется неравенство
| φ' (x)|≤q<1, причем φ' (x)>0, то последовательностные приближения
φ(xn-1)=xn (n є N , x0 є [a,b]) сходятся к корню монотонно . В том же случае , если φ' (x)<0 , то последовательные приближения колеблются около точного значения корня ξ.
Проверкой точности является следующее соотношение
|ξ- xn |≤(q/(1-q))| xn – xn-1 |, где «q» определяется из выражения | φ' (x)|≤q<1.
Если ставится условие , что истинное значение корня ξ должно отличатся от приближенного значения на величину Δ , то |ξ- xn |≤Δ и | xn – xn-1 |≤Δ((1-q)/q)
Пример
Методом итераций уточнить до 10^(-4) корень уравнения 5х³ - 20х² +3=0 , заключенный на отрезке [0,1].
Решение
Данное уравнение следует привести к виду х= φ(x) .Это можно сделать по разному, например:
х=х+(5х²-20х+3), где φ1(x)=5х²-19х+3;
х=((20х-3)/20)^(1/3) , где φ2(x) =((20х-3)/20)^(1/3);
х=((5х³+3)/20) , где φ3(x)=((5х³+3)/20)
Поскольку условие достаточности | φ' (x)|≤q<1 характеризует сходимость итерационного процесса ,то определим φj(x) для вычисления последовательных приближений :
| φ'1 (x)|=|15x²-19|>1 на [0,1] ;
| φ'2 (x)|=|(1/3)*(( (25)^(1/3) *4) / ((20x-3)^(2)) ^(1/3))|>0 на [0,1] ;
| φ'3 (x)|=|((15х²)/20)|=(3/4)x²<1 на [0,1] ;
Следовательно , можно воспользоваться функцией φ3(x) для ?????? приближенного корня по формуле :
Xn = (5х³n-1 +3)/20
За начальное приближение возьмем max φ'(x) на [0,1] , т.е. х0=0,75=q
Пользуясь формулой | xn – xn-1 |≤(ε*(1-q))/q,
Определим какой должна быть разность | xn – xn-1 | ,что бы была достигнута заданная конечность , т.е.
| xn – xn-1 |≤(0,0001(1-0,75))/0.75=0.00003
Таким образом когда обсолютная величина разности | xn – xn-1 | не превзойдет 0,00003 , итерационный процесс следует прекратить и считать заданную точность достигнутой.
Вычисления сведем в таблицу:
|
xn |
х³n |
Xn+1 = φ(xn) |
|
0.75 |
0.42188 |
0.25547 |
|
0.25547 |
0.016777 |
0.154144 |
|
0.154144 |
0.005652 |
0.151413 |
|
0.151413 |
0.005443 |
0.151361 |
|
0.151361 |
0.005442 |
0.151361 |
Из этой таблицы
х4 – x5=0,1541413-0,151361=0,0000 , т.е.
ξ=0,151361
Пример
Найти методом итераций наименьший положительный корень( с пятью значащими цифрами) уравнения !
Cos(x ) –(1/x)sin(x)=0.
Решение
Заменяем исходное уравнение эквивалентным ему: х=tg(x) и построив график функции y1=x; y2=tg(x), находим что х0=(3π)/2=4.7.
Однако к уравнению х=tg(x) непосредственно метод итераций применить нельзя, т.к. при любом значении х φ' (x)=( tg(x))'=(1/cos²(x)) больше единице (т.е. не соблюдается достаточное условие сходимости итерационного процесса | φ' (x)<1| ).
Поэтому перейдем к обратным функциям , т.е. к уравнению
φ' (x)=(arctg(x))'=(1/(1+x²))<1 при x≠0
Уравнением x= arctg(x), эквивалентное исходному уравнению
Cos(x ) –(1/x)sin(x)=0, решаем при помощи формулы
Xn =arctg(xn-1) , где х0=4,7
Итерационный процесс заканчиваем тогда, когда с необходимой точностью совпадут значения xn и xn-1
Выполнив вычисления приведенные в таблице
|
n |
0 |
1 |
2 |
3 |
|
xn |
4.7 |
4,50 |
4,94 |
4,4934 |
|
Arctg(xn) |
4.50 |
4.494 |
4.4934 |
4.4934 |
Получаем х=4,4934
Пример
Вычислит с точностью до ε=10^(-5) корень уравнения (е^(x))-x²=0
Решение
Перепишем заданное уравнение в виде (е^(x))=x²
И отделим корни графически
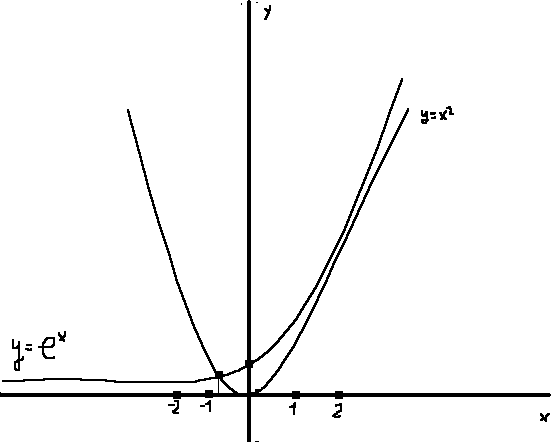 Единственный
корень уравнения (е^(x))-x²
лежит в интервале [-0.8;-0.7]
Единственный
корень уравнения (е^(x))-x²
лежит в интервале [-0.8;-0.7]
Действительно :
f(-0,8)= (е^(-0,8))-0,8²=0,44933-0,64=-0,19607<0 ,
f(-0,7)= (е^(-0,7))-0,7²=0,49659-0,49=0,00659>0 ,
т.е. f(-0.8)*f(-0.7)<0.
Методом проб сузим интервал[a,b]. В котором находится корень ξ .
Имеем : [-0.725;-0.7].
Из уравнения(е^(x))-x²=0 получаем х=-((е^х)^(1/2)) (пер знаком радикала стоит знак минус, т.к. известно, что корень ξ отрицателен ).
Проверим каким является итерационный процесс для функции
φ(x)= -(х/(e^2))
φ'(x)=-(1/2)e^(x/2); | φ'(-0.725)|=0.34727;
|φ' (-0.7)|=0.35230,
Поскольку |φ' (x)|<1 ,на [-0.725;-0.7] , то итерационный процесс сходится, т.е. удовлетворяется требование |φ'(x)|≤q<1.
Возьмем q=0.36 ,а т.к.ε=10^(-5), то из(q/(1-q)) | xn – xn-1| ≤ε получаем
| xn – xn-1|≤ ε((1-q)/q) и | xn – xn-1|≤10^(-5)(1-0.36)/(0.36)=18*10^(-5)
Таким образом, требуемая точность будет достигнута, если выполняется неравенство | xn – xn-1| ≤ 0.00002 .
В качестве нулевого приближения можно взять любую точку отрезка
[-0.725;-0.7]. Примем х0=-0,7.
Вычисления сведем в таблицу
|
n |
xn |
xn/2 |
e^( xn/2) |
|
0 |
-0.7 |
-0.35 |
-0.70460 |
|
1 |
-0.70460 |
-0.35230 |
-0.70307 |
|
2 |
-0.70307 |
-0.35154 |
-0.70360 |
|
3 |
-0.70360 |
-0.35180 |
-0.70342 |
|
4 |
-0.70342 |
-0.35171 |
-0.70348 |
|
5 |
-0.70348 |
-0.35174 |
-0.70346 |
|
6 |
-0.70346 |
|
|
Т.к. | x6 – x5|=|-0.70346+0.70348|=0.00002 , то ξ≈-0,70346
Методы решения систем линейных уравнений.
Решение матричных уравнений.
Матричное уравнение
![]() ,
где А - собственная матрица, Х –
вектор-столбец неизвестных, В –
вектор-столбец свободных членов системы:
,
где А - собственная матрица, Х –
вектор-столбец неизвестных, В –
вектор-столбец свободных членов системы:
А=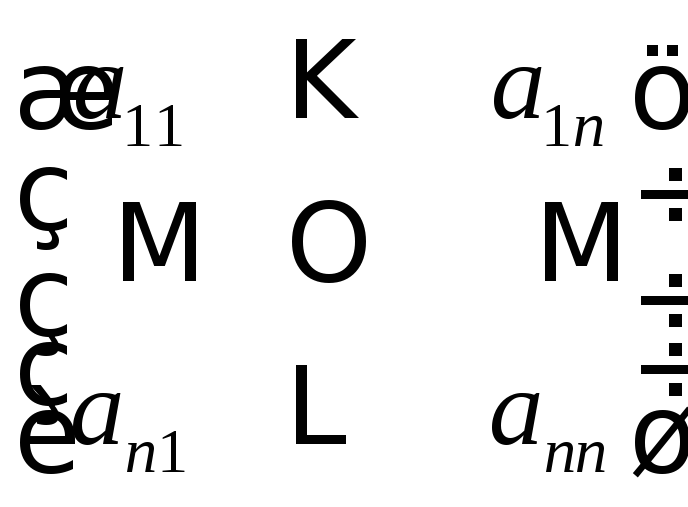 ,
Х=
,
Х=![]() ,
В=
,
В=![]() ,
решается умножением обеих его частей
на обратную матрицу
,
решается умножением обеих его частей
на обратную матрицу![]() :
:
![]()
Поскольку
![]() (где
Е – единичная матрица), то
(где
Е – единичная матрица), то![]() .
Отсюда
.
Отсюда![]() .
.
Нахождение обратной матрицы называется обращением данной матрицы. Обратную матрицу
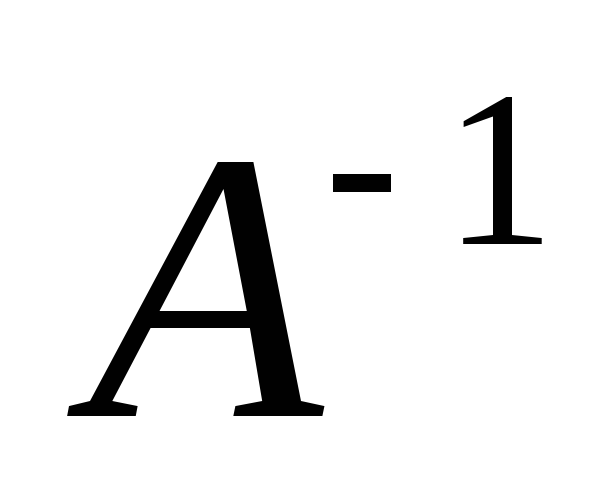 неособенной матрицы А (т.е. если
неособенной матрицы А (т.е. если
 )
находят по следующей схеме:
)
находят по следующей схеме:
Вычисляют определитель -
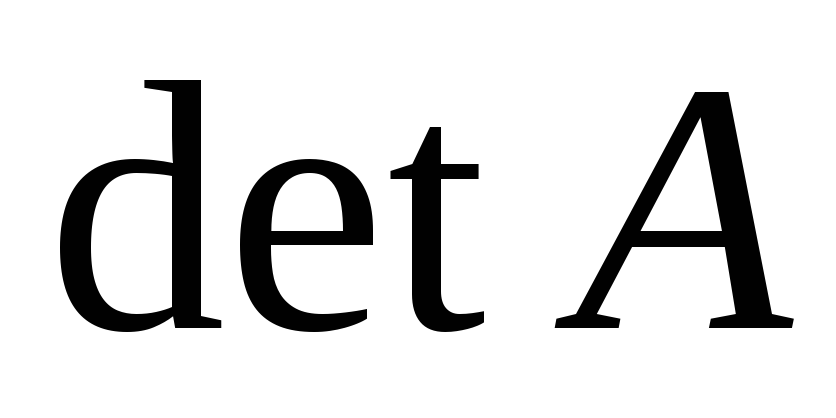 ;
;Вычисляют алгебраические дополнения к элементам матрицы А и составляют матрицу, союзную по отношению к данной
 ;
;Находят обратную матрицу по формуле
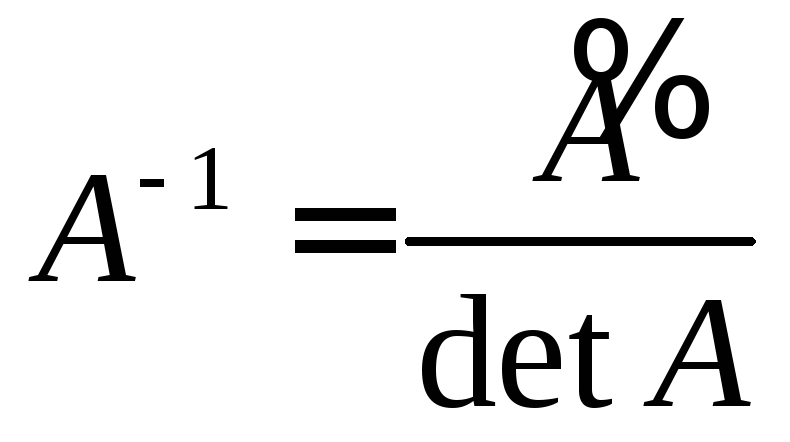 .
.
Союзная
матрица
![]() по отношению к данной матрице А есть
транспонированная матрица алгебраических
по отношению к данной матрице А есть
транспонированная матрица алгебраических![]() всех элементов матрицы А:
всех элементов матрицы А:
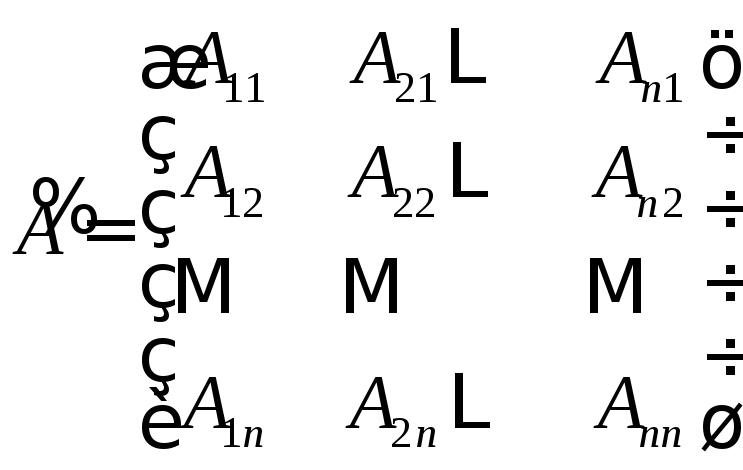
Пример: Используя матричную запись, решить систему линейных уравнений:

Решение:
Имеем
![]() ,
т.е.:
,
т.е.:
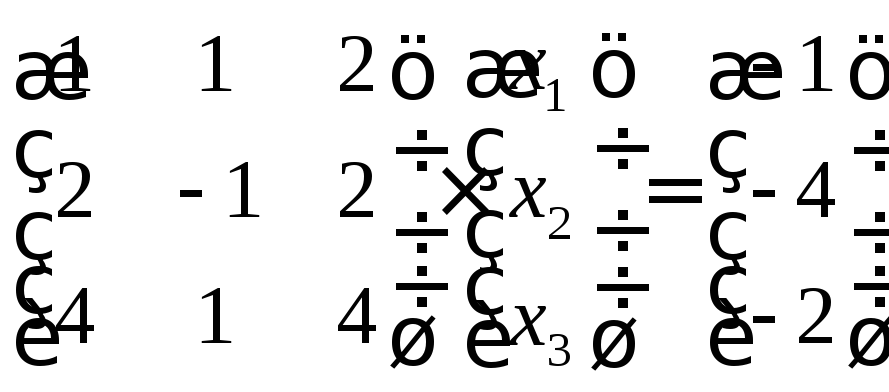 Находим
Находим
![]() :
: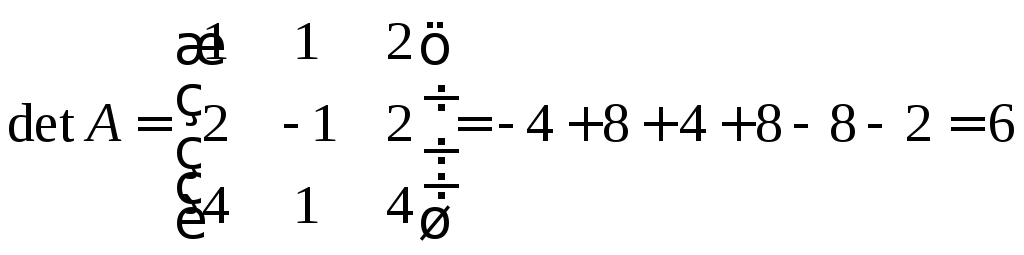 ;
;
![]() ;
;
![]()
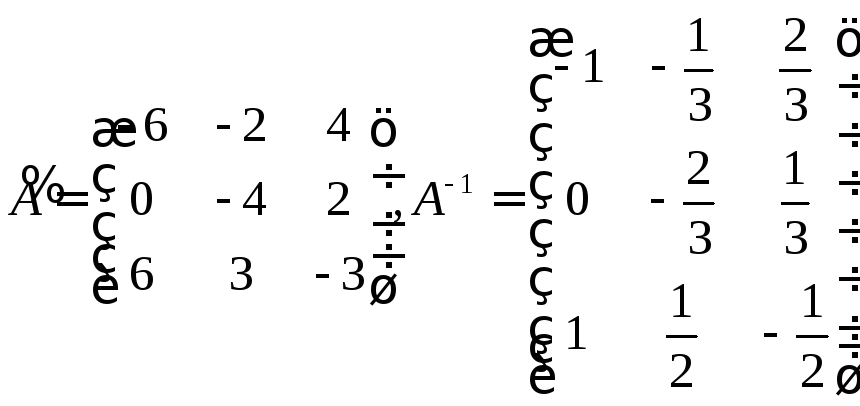 .
Поскольку
.
Поскольку
![]() ,
то
,
то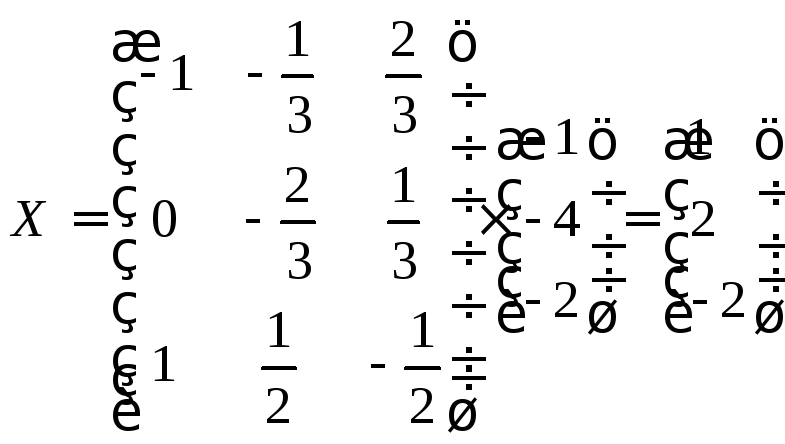 .
Отсюда
.
Отсюда![]()
Замечание:
Если
порядок матрицы А большой, то рассмотренный
метод обращенной матрицы требует сложной
вычислительной работы. Пользуясь
разложением квадратной матрицы А на
произведение двух треугольных, можно
легко вычислить обратную матрицу
![]() ,
а именно, если
,
а именно, если![]() ,
то
,
то![]() .
В этом случае обратные матрицы
.
В этом случае обратные матрицы![]() для треугольных матриц
для треугольных матриц![]() находятся
сравнительно просто (обратная матрица
неособенной треугольной матрицы есть
такая же треугольная матрица того же
типа и структуры). Отметим, что если
квадратная матрица А имеет отличные от
нуля диагональные миноры (это миноры
определителя матрицы, на главных
диагоналях которых стоят диагональные
элементы матрицы), т.е.:
находятся
сравнительно просто (обратная матрица
неособенной треугольной матрицы есть
такая же треугольная матрица того же
типа и структуры). Отметим, что если
квадратная матрица А имеет отличные от
нуля диагональные миноры (это миноры
определителя матрицы, на главных
диагоналях которых стоят диагональные
элементы матрицы), т.е.:
 что
ее можно разложить на произведение двух
треугольных матриц (верхней и нижней).
Это разложение единственно, если
диагональным элементам одной из
треугольных матриц заранее дать отличные
от нуля значения (например, положить их
равными единице).
что
ее можно разложить на произведение двух
треугольных матриц (верхней и нижней).
Это разложение единственно, если
диагональным элементам одной из
треугольных матриц заранее дать отличные
от нуля значения (например, положить их
равными единице).
Искомые
элементы треугольных матриц
![]() находят следующим образом:
находят следующим образом:
Перемножают матрицы
 ;
;Приравнивают соответствующие элементы матрицы-произведения
 элементам заданной матрицы А, а именно
элементам заданной матрицы А, а именно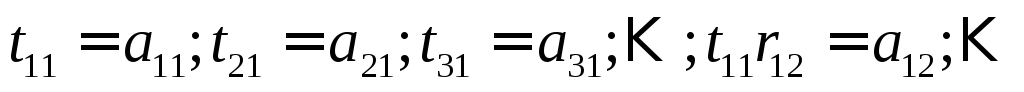 - решают сначала одночленные, затем
двучленные и т.д. уравнения.
- решают сначала одночленные, затем
двучленные и т.д. уравнения.
Пример:
Для
матрицы
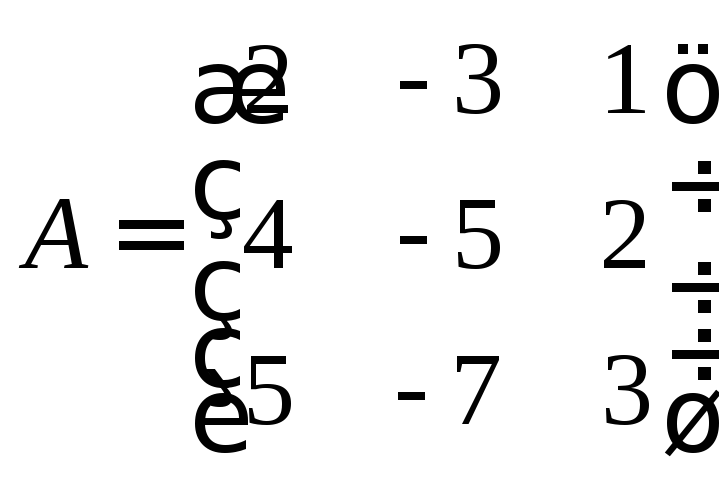 найти обратную, разложив данную матрицу
на произведение двух треугольных.
найти обратную, разложив данную матрицу
на произведение двух треугольных.
Решение:
Вычисляем:
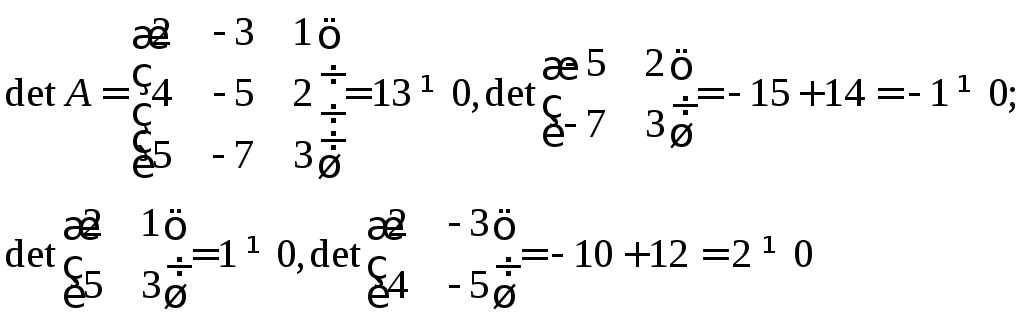
Т.е.
А можно представить как
![]() ,
т.е.:
,
т.е.:
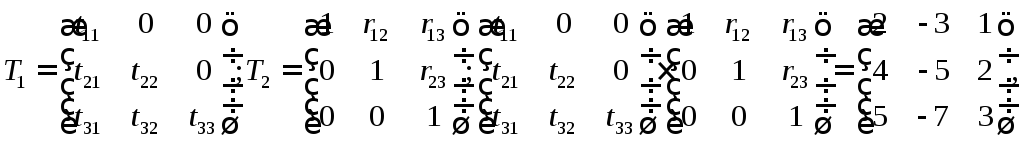 или
или
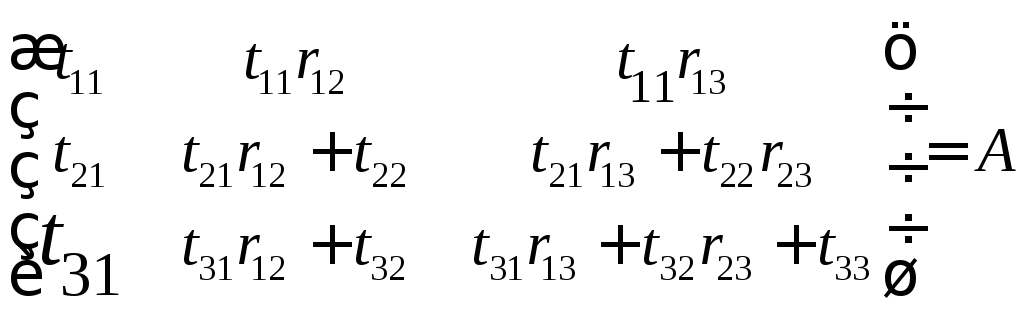
Составляем уравнения:
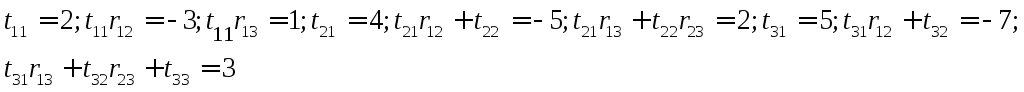
Решая эти уравнения, находим:
![]() .
Следовательно:
.
Следовательно:
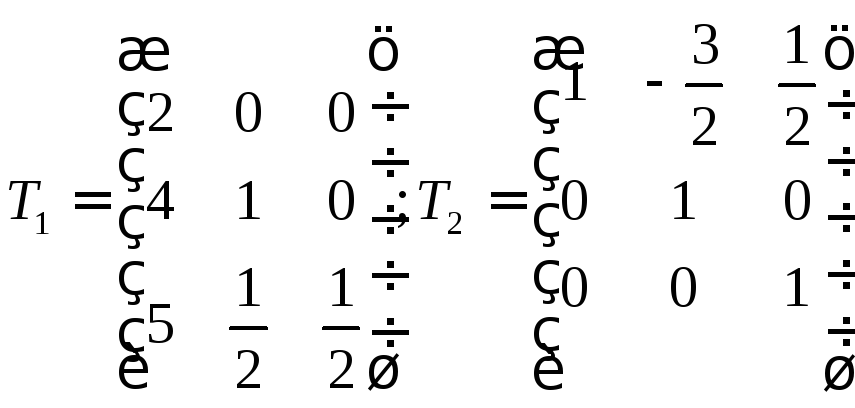 .
Для нахождения обратной матрицы
.
Для нахождения обратной матрицы
![]() найдем
найдем![]() .
Пусть
.
Пусть![]() =
= ,
тогда
,
тогда![]() ,
или
,
или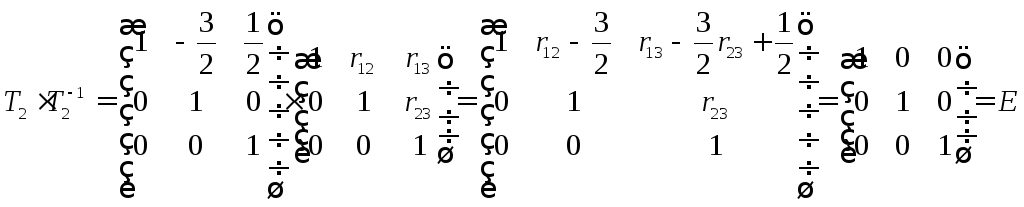
Составляем
уравнения:
![]() ,
отсюда находим:
,
отсюда находим:![]() .
Следовательно:
.
Следовательно: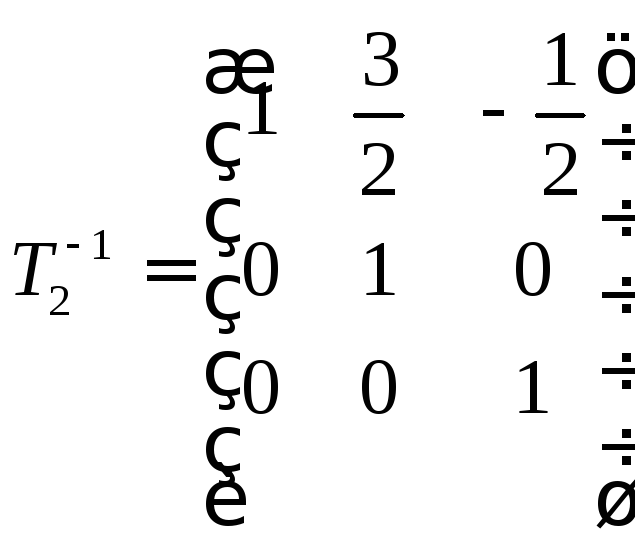 .
Найдем
.
Найдем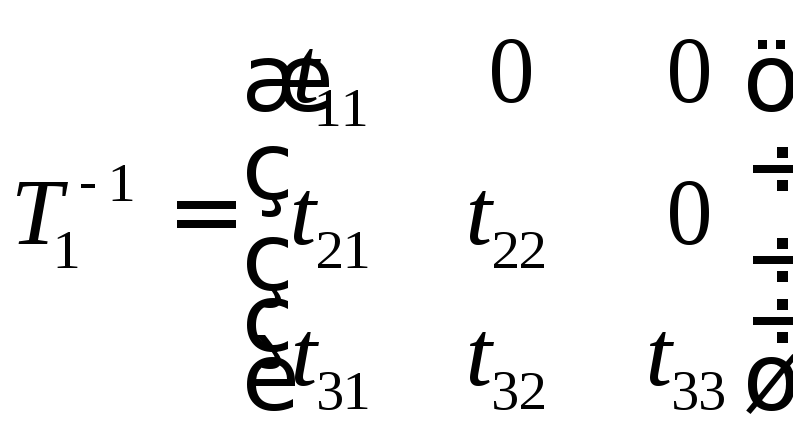 ,
учитывая, что
,
учитывая, что![]() :
:
![]() ,
отсюда находим элементы обратной матрицы
,
отсюда находим элементы обратной матрицы
![]() :
:
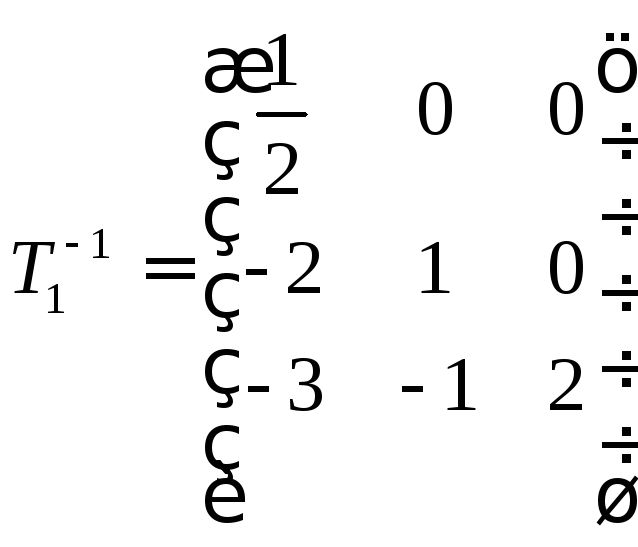 .
Обратная матрица
.
Обратная матрица
![]() :
: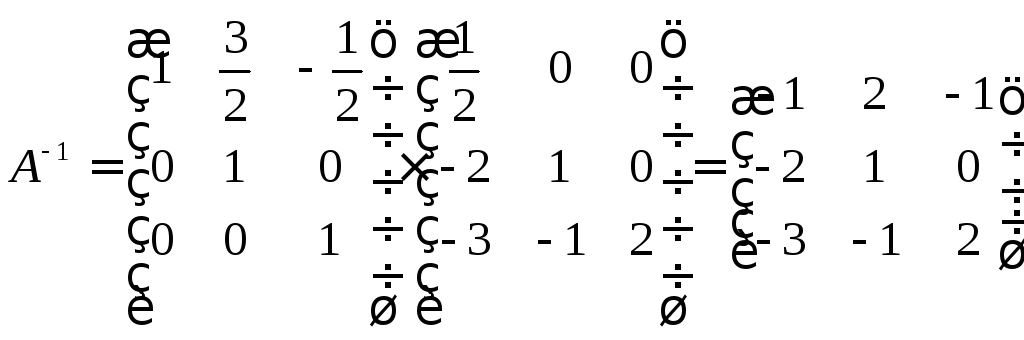
Формулы Крамера для решения системы линейных уравнений.
Если
определитель
![]() квадратной системы линейных уравнений
квадратной системы линейных уравнений![]() не равен нулю, то эта система имеет
единственное решение и это решение
находиться по формулам Крамера:
не равен нулю, то эта система имеет
единственное решение и это решение
находиться по формулам Крамера:![]() где
где![]() ,
,![]() - определитель, получаемый из
- определитель, получаемый из![]() заменой к-ого столбца на столбец свободных
членов
заменой к-ого столбца на столбец свободных
членов![]() .
.
Пример:
Решить по формулам Крамера систему линейных уравнений:
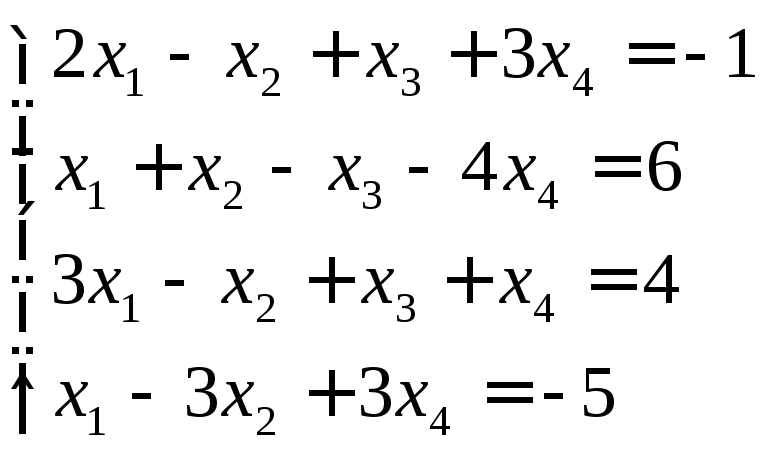
Решение.
Находим определители
![]() ,
раскладывая их на миноры по элементам
последней строки:
,
раскладывая их на миноры по элементам
последней строки: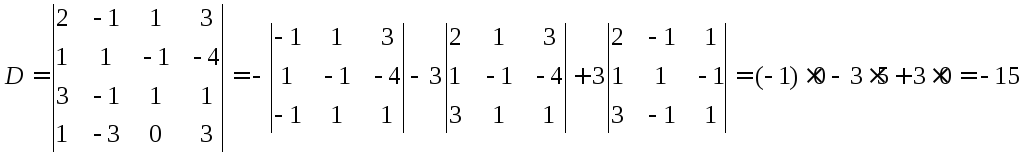 (здесь
первый и третий миноры равны нулю, т.к.
имеют пропорциональные столбцы).
(здесь
первый и третий миноры равны нулю, т.к.
имеют пропорциональные столбцы).
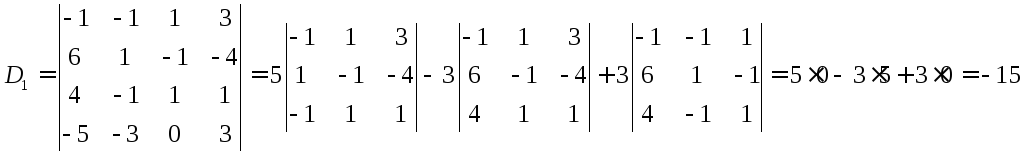
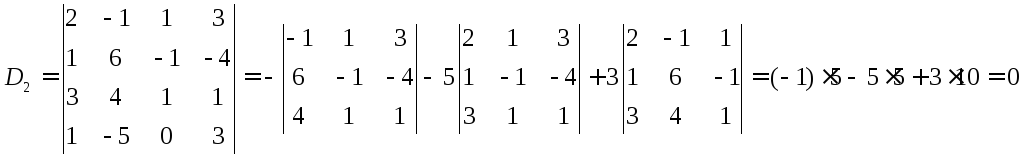
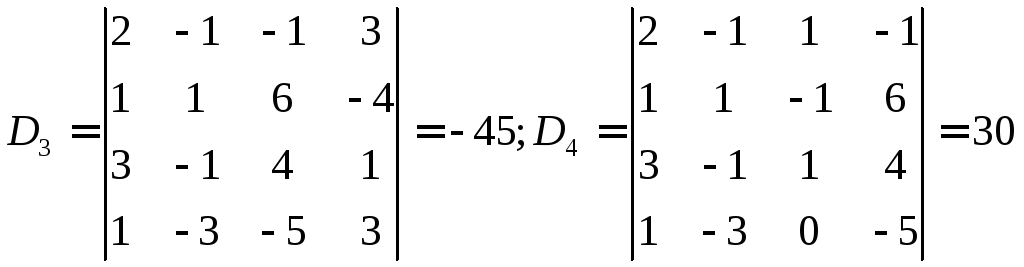
Теперь
по формулам Крамера получаем решение
системы:
![]()
Замечание. Решение линейных неоднородных уравнений большой размерности по формулам Крамера очень громоздко. На практике такие системы решают другими методами. Наиболее распространенным методом среди них является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных (в результате чего, данная система уравнений преобразуется к эквивалентной системе, решение которой не составляет труда).
Решение системы уравнений методом Гаусса (методом последовательного исключения неизвестных)
Метод Гаусса – прямой (точный) метод решения совместных систем линейных уравнений, дающий возможность получить решение посредством конечного числа арифметических действий.
Процесс решения системы уравнений методом Гаусса состоит из прямого и обратного хода.
Прямой ход – преобразование заданной системы уравнений к эквивалентной системе с верхней треугольной матрицей.
Обратный ход – получение решения системы.
Пример.
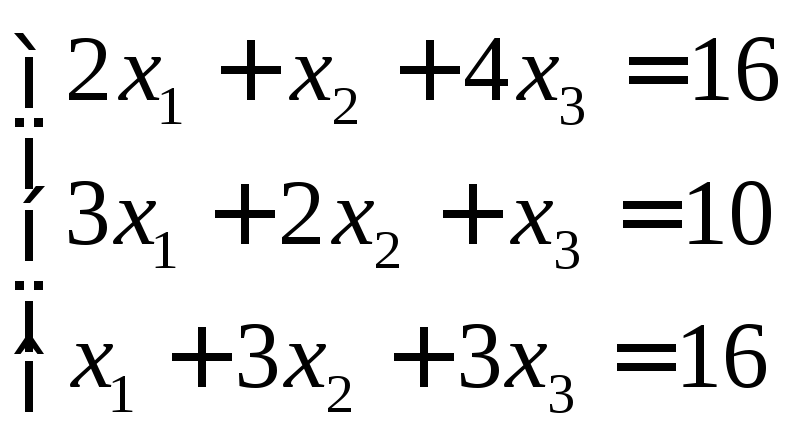
Поскольку
эта система совместна, т.е.
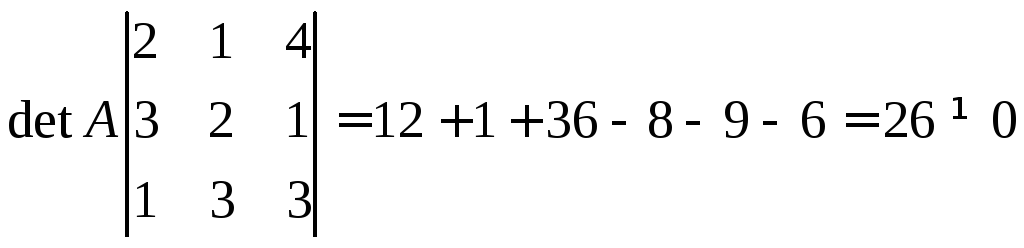 ,
а число переменных ровно числу уравнений,
(т.е. система является определенной
системой 3-его порядка), то ее решение
единственно. Прямой ход включает
следующие преобразования расширенной
матрицы:
,
а число переменных ровно числу уравнений,
(т.е. система является определенной
системой 3-его порядка), то ее решение
единственно. Прямой ход включает
следующие преобразования расширенной
матрицы:
Преобразованная система уравнений имеет вид:
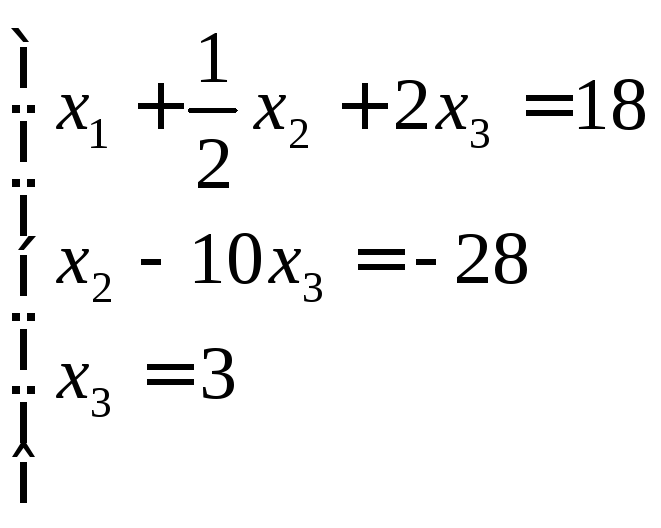 Обратный
ход:
Обратный
ход:
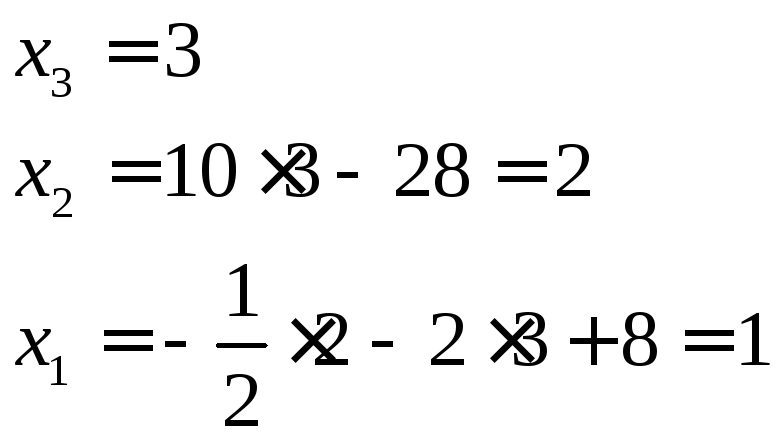
а) схема единственного деления.
Операции прямого и обратного хода удобно вести по вычислительной схеме единственного деления. Как для системы 3-х уравнений с 3-мя неизвестными имеем вычислительную схему:
|
ходы
|
№ строки
|
Коэффициенты
при
|
Свобоныые члены |
Контроль | |||
|
|
|
|
Контрольные суммы |
Строчные суммы | |||
|
Прямой ход
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
| |
|
3 |
|
|
|
|
|
| |
|
4 |
1 |
|
|
|
|
| |
|
5 |
- |
|
|
|
|
| |
|
6 |
- |
|
|
|
|
| |
|
7 |
- |
1 |
|
|
|
| |
|
8 |
- |
- |
|
|
|
| |
|
9 |
- |
- |
1 |
|
|
| |
|
Обратный ход |
10 |
- |
- |
1 |
|
|
|
|
11 |
- |
1 |
- |
|
|
| |
|
12 |
1 |
- |
- |
|
|
| |
В
этой схеме:
![]() - ведущий элемент;
- ведущий элемент;![]() ;
;![]() -
ведущий элемент;
-
ведущий элемент;![]() ;
;![]() ;
;![]() - контрольные суммы, над которыми
выполняются те же действия, что и над
остальными элементами строки.
- контрольные суммы, над которыми
выполняются те же действия, что и над
остальными элементами строки.
Пример.
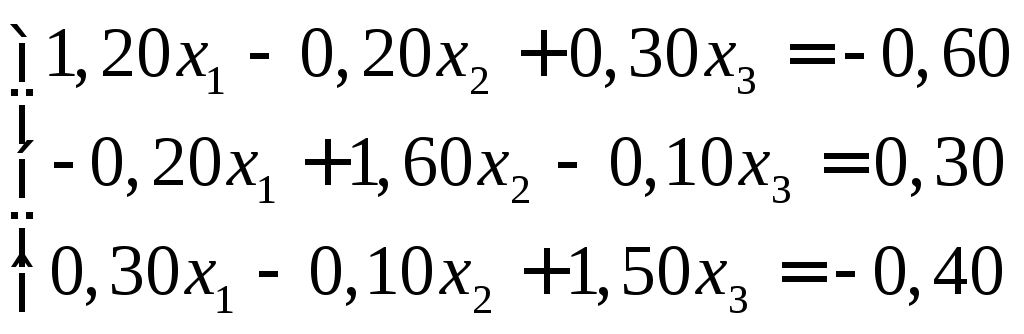
По схеме единственного деления решение этой системы уравнений проводиться в следующей последовательности:
1) в первые три строки схемы единственного деления вписываются коэффициенты и свободные члены каждого уравнения данной системы и для этих строк выписываются контрольные и строчные суммы (на этом этапе эти суммы совпадают между собой; на следующем этапе они будут служить целям контроля);
2)
делим все числа первой строки на ведущий
элемент
![]() ,
или, что удобнее, умножаем их на число,
обратное ведущему элементу:
,
или, что удобнее, умножаем их на число,
обратное ведущему элементу:![]() (далее всюду в промежуточных результатах
будем сохранять два запасных десятичных
знака).
(далее всюду в промежуточных результатах
будем сохранять два запасных десятичных
знака).
Округляя полученные произведения до четырех десятичных знаков, выписываем их в четвертую строку таблицы.
Так,
![]() .
.
Строчная сумма четвертой строки равна 1-0,1667+0,2500-0,5000=0,5833, а контрольная сумма (1,20-0,20+0,30-0,60)*0,8333=0,70*0,8333=0,5833. Совпадение строчной и контрольной сумм означает отсутствие вычислительных ошибок.
3)
вычислив коэффициенты
![]()
![]() вычислительной системы
вычислительной системы
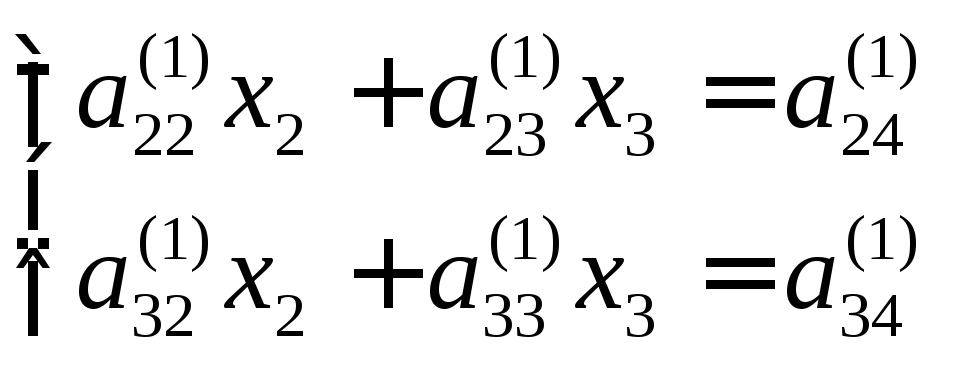 ,
где
,
где
![]() .
Заполним строки 5 и 6 схемы единственного
деления. Очевидно:
.
Заполним строки 5 и 6 схемы единственного
деления. Очевидно: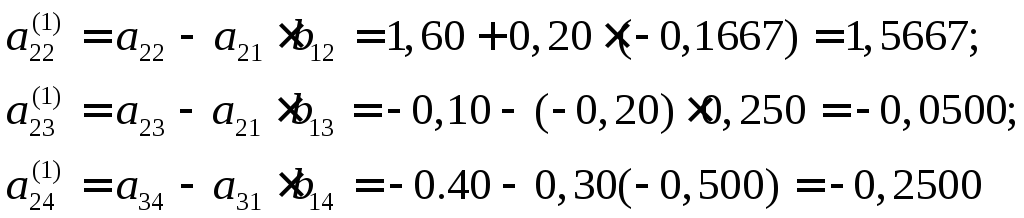
4) повторяем процесс, т.е. строки 7 и 9 заполняем по тому же правилу, что и строки 4 и 8 – по правилу заполнения строк 5 и 6. Текущий контроль вычислений осуществляется вычислением контрольных сумм и сравнением их со строчными для каждой строки
|
Ходы |
№ строки |
Коэффициенты
при
|
Свободные члены |
Контроль | |||
|
|
|
|
Контрольные суммы |
Строчные суммы | |||
|
Прямой ход
|
1 |
1,20 |
-0,20 |
0,30 |
-0,60 |
0,70 |
0,70 |
|
2 |
-0,20 |
1,60 |
-0,10 |
0,30 |
1,60 |
1,60 | |
|
3 |
0,30 |
-0,10 |
1,50 |
-0,40 |
1,30 |
1,30 | |
|
4 |
1 |
-0,1667 |
0,2500 |
-0,5000 |
0,5833 |
0,5833 | |
|
5 |
- |
1,5667 |
-0,0500 |
0,2000 |
1,7168 |
1,7168 | |
|
6 |
- |
-0,5000 |
1,4250 |
-0,2500 |
1,1250 |
1,1250 | |
|
7 |
- |
1 |
-0,0319 |
0,1276 |
1,0957 |
1,0957 | |
|
8 |
- |
- |
1,4234 |
-0,2436 |
1,1798 |
1,1798 | |
|
9 |
- |
- |
1 |
-0,1711 |
0,8289 |
0,8289 | |
|
Обратный ход |
10 |
- |
- |
1 |
-0,1711 |
0,8289 |
0,8289 |
|
11 |
- |
1 |
- |
0,1221 |
1,1221 |
1,1221 | |
|
12 |
1 |
- |
- |
-0,4368 |
0,5631 |
0,5632 | |
5)
числа, заполняющие 4, 7 и 9 строки схемы,
представляют собой коэффициенты и
свободные члены простейшей системы
трех уравнений:
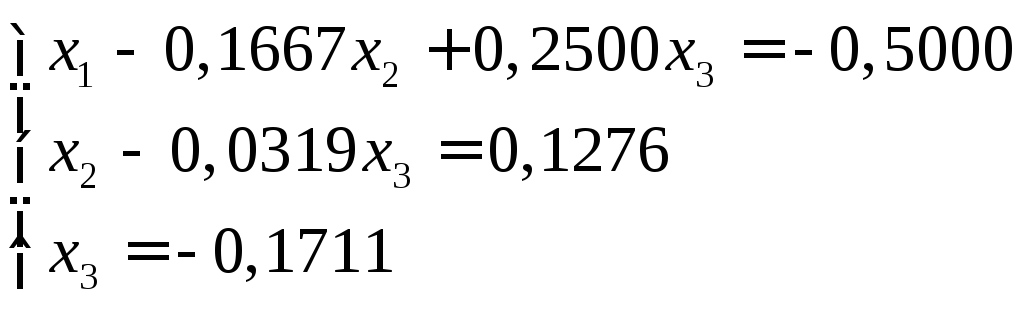 эквивалентной
данной. Решение этой системы осуществляется
по формулам обратного хода:
эквивалентной
данной. Решение этой системы осуществляется
по формулам обратного хода:
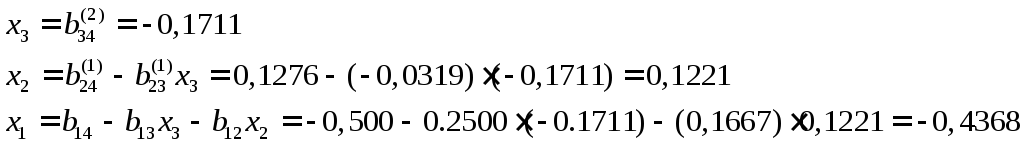
Для
контроля обратного хода вычисляют числа
![]() ,
которые должны быть связаны с найденным
решением данные системы соотношениями:
,
которые должны быть связаны с найденным
решением данные системы соотношениями:![]() .
.
Действительно,
решение данной системы![]() связано с решением системы
связано с решением системы![]() указанной
зависимости
указанной
зависимости![]()
![]() и
учитываем, что
и
учитываем, что
![]() )
)
Хорошее
совпадение контрольных и строчных сумм
в рассмотренном примере говорит о том,
что запасных знаков было удержано
достаточно. Округляя найденные значения
![]() окончательно
получаем:
окончательно
получаем:![]() .
.
Б) Схема с выбором главного элемента. Эту схему вычислений, лучшей по точности из всех вычислительных схем по методу Гаусса, проиллюстрируем на этом же примере. Первые три строки схемы, за исключением третьего столбца, заполняются аналогично схеме единственного деления:
|
Ходы |
№ строки |
|
Коэффициенты
при
|
Свободные члены |
Контроль | |||
|
|
|
|
Контрольные суммы |
Строчные суммы | ||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Прямой ход |
1 |
0,125 |
1,20 |
-0,20 |
0,30 |
-0,60 |
0,70 |
0,70 |
|
2 |
-1 |
-0,20 |
1,60 |
-0,10 |
0,30 |
1,60 |
1,60 | |
|
3 |
0,062 |
0,30 |
-0,10 |
1,50 |
-0,40 |
1,30 |
1,30 | |
Выбираем
в таблице наибольший по модулю коэффициент
![]() (который будем называть главным
элементом). Имеем
(который будем называть главным
элементом). Имеем![]() =1,60
(в таблице выделен цветом). В третьем
столбце выписываются взятые с обратным
знаком частные от деления на главный
элемент
=1,60
(в таблице выделен цветом). В третьем
столбце выписываются взятые с обратным
знаком частные от деления на главный
элемент![]() всех элементов столбца, содержащего
главный элемент (в данном случае пятого
столбца). Прибавляя теперь к каждой из
строк схемы (столбцы 4-8) строку с главным
элементом, умноженную предварительно
на соответствующий множитель и третьего
столбца, получим:
всех элементов столбца, содержащего
главный элемент (в данном случае пятого
столбца). Прибавляя теперь к каждой из
строк схемы (столбцы 4-8) строку с главным
элементом, умноженную предварительно
на соответствующий множитель и третьего
столбца, получим:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Прямой ход |
4 |
0,193 |
1,175 |
- |
0,288 |
-0,563 |
0,900 |
0,900 |
|
5 |
-1 |
0,288 |
- |
1,494 |
0,381 |
1,399 |
1,401 |
Здесь контроль производиться так же, как и в схеме единственного деления.
Выполненные
действия привели к исключению из исходной
системы неизвестной
![]() .
В оставшейся системе (строки 4 и 5) выбираем
новый главный элемент (это коэффициент
при
.
В оставшейся системе (строки 4 и 5) выбираем
новый главный элемент (это коэффициент
при![]() ,
т.е. 1,494).
,
т.е. 1,494).
Все последующие действия выполняются аналогично предыдущим, т.е. получаем:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Прямой ход |
6 |
|
1,119 |
- |
- |
-0,489 |
0,630 |
0,630 |
В
результате последней операции исключена
неизвестная
![]() ,
и прямой ход завершен.
,
и прямой ход завершен.
Строки, содержащие последовательно выбираемые главные элементы, - строки 2, 5 и 6 дают систему, эквивалентную данной:
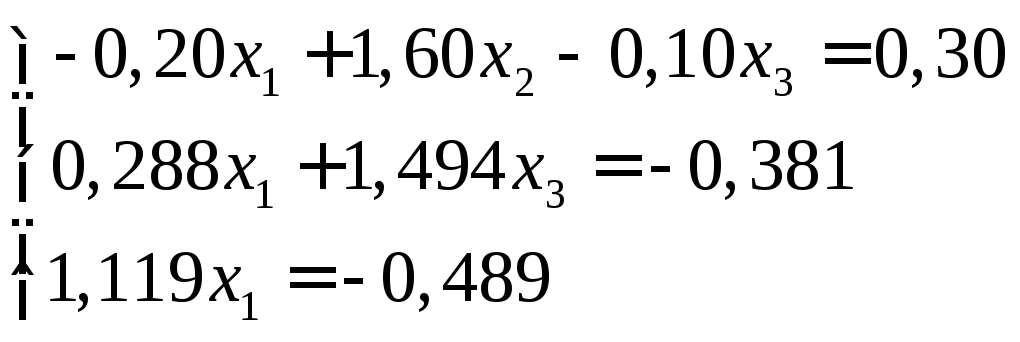
Обратный ход:
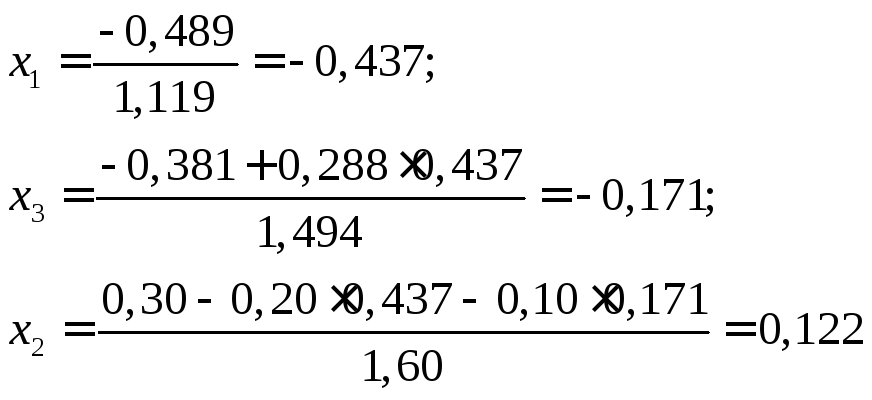
Полностью схема с выбором главного элемента для нашего примера имеет вид:
|
Ходы |
№ строки |
|
Коэффициенты
при
|
Свободные члены |
Контроль | |||
|
|
|
|
Контрольные суммы |
Строчные суммы | ||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Прямой ход
|
1 |
0,125 |
1,20 |
-0,20 |
0,30 |
-0,60 |
0,70 |
0,70 |
|
2 |
-1 |
-0,20 |
1,60 |
-0,10 |
0,30 |
1,60 |
1,60 | |
|
3 |
0,062 |
0,30 |
-0,10 |
1,50 |
-0,40 |
1,30 |
1,30 | |
|
4 |
-0,193 |
1,175 |
- |
0,288 |
-0,563 |
0,900 |
0,900 | |
|
5 |
-1 |
0,288 |
- |
1,494 |
-0,381 |
1,399 |
1,401 | |
|
6 |
|
1,119 |
- |
- |
0,489 |
0,630 |
0,630 | |
|
7 |
|
1 |
- |
- |
-0,437 |
0,563 |
0,563 | |
|
8 |
|
- |
- |
1 |
-0,171 |
0,828 |
0,829 | |
|
9 |
|
- |
1 |
- |
0,122 |
1,122 |
1,122 | |
Округляя
запасной знак, окончательно получаем:
![]() =-0,44;
=-0,44;![]() =-0,12;
=-0,12;![]() =-0,17.
=-0,17.
Итерационные методы решения систем линейных уравнений.
В отличие от прямых (точных) методов, итерационные методы являются бесконечно повторяющимися процессами. Если этот процесс сходящийся, то на каждом последующем шаге получается более точное приближение к искомому решению данной системы уравнений.
а) Метод простой итерации.
Для
итерационных методов систему линейных
уравнений
![]() приводят к виду
приводят к виду![]()
![]() .
В качестве начального приближения
.
В качестве начального приближения![]() целесообразно взять свободные члены
целесообразно взять свободные члены![]() системы, а дальнейшиеk-
ые приближения строить по формулам:
системы, а дальнейшиеk-
ые приближения строить по формулам:
![]()
Если
каждая из последовательностей приближений
![]() имеет предел
имеет предел![]() ,
то совокупность чисел
,
то совокупность чисел![]() является решением заданной системы.
является решением заданной системы.
Действительно,
так как
![]() .
.
б) Достаточный признак сходимости итерационного процесса.
Если
максимальная сумма модулей коэффициентов
при неизвестных
![]() каждого уравнения системы меньше
единицы, т.е.
каждого уравнения системы меньше
единицы, т.е.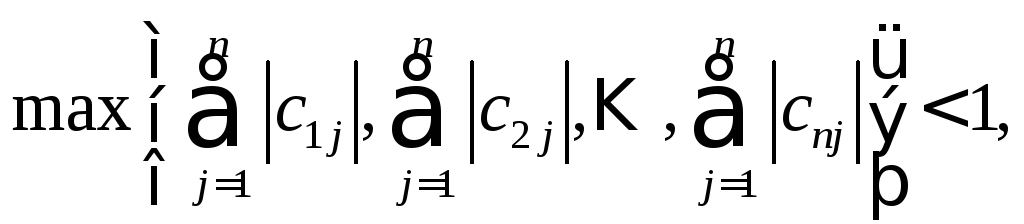 то процесс итерации сходится.
то процесс итерации сходится.
Пример: Исследовать систему уравнений на сходимость итерационного процесса.
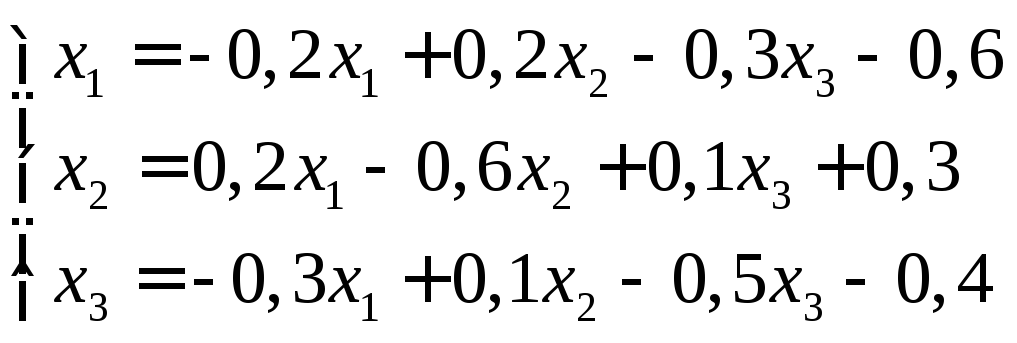
Решение.
Имеем:
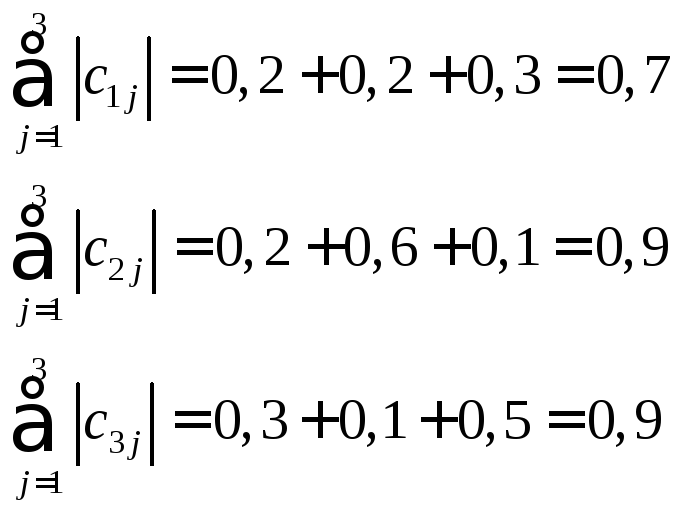
Проверка:
![]() ,
то итерационный процесс для заданной
системы трех уравнений сходиться.
,
то итерационный процесс для заданной
системы трех уравнений сходиться.
в) Решение системы уравнений методом простой итерации.
Рассмотрим пример решения систем уравнений методом итерации:
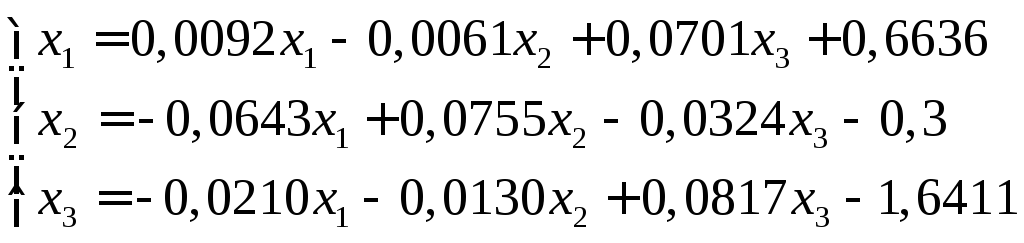
предполагая, что абсолютные погрешности коэффициентов и свободных членов системы не превышают 0,00005.
Решение.
Для заданной системы уравнений удовлетворяется условие достаточности сходимости итерационного процесса.
Примем
за начальные приближения решения
![]() свободные члены системы:
свободные члены системы:
![]()
Последующие вычисления приближений выполняем по формулам:
![]() Результат
вычислений сведем в таблицу:
Результат
вычислений сведем в таблицу:
|
Приближенно |
Коэффициенты
при
|
Свободные члены | ||
|
|
|
| ||
|
|
0,0092 |
-0,0061 |
0,0701 |
0,6636 |
|
|
-0,0634 |
0,0755 |
-0,0324 |
-0,8172 |
|
|
-0,0210 |
-0,0130 |
0,0817 |
-1,6411 |
|
|
0,636 |
-0,8172 |
-1,6411 |
|
|
|
0,55974 |
-0,86838 |
-1,77849 |
|
|
|
0,54937 |
-0,86119 |
-1,78657 |
|
|
|
0,54866 |
-0,85966 |
-1,78740 |
|
|
|
0,54859 |
-0,85948 |
-1,78747 |
|
|
|
0,54859 |
-0,85945 |
-1,78749 |
|
|
|
0,54859 |
-0,85945 |
-1,78749 |
|
В данном случае пятое и шестое приближения решения системы имеют пять одинаковых десятичных знаков. Округляя запасной знак, окончательно имеем:
![]()
г) О приведении линейной системы к виду, пригодному к методу итерации.
Для любой системы с невырожденной матрицей существуют сходящиеся итерационные методы решения. Однако, не всегда эти методы удобны для практических вычислений.
Поэтому
приведение системы линейных уравнений
![]() к виду
к виду![]() должно осуществляться так, чтобы
выполнялся признак достаточности
должно осуществляться так, чтобы
выполнялся признак достаточности![]() .
.
В
том случае, если диагональные элементы
матрицы А отлична от нуля, т.е.
![]()
![]() ,
и
,
и![]()
![]() :
то систему
:
то систему![]() можно записать в виде:
можно записать в виде:
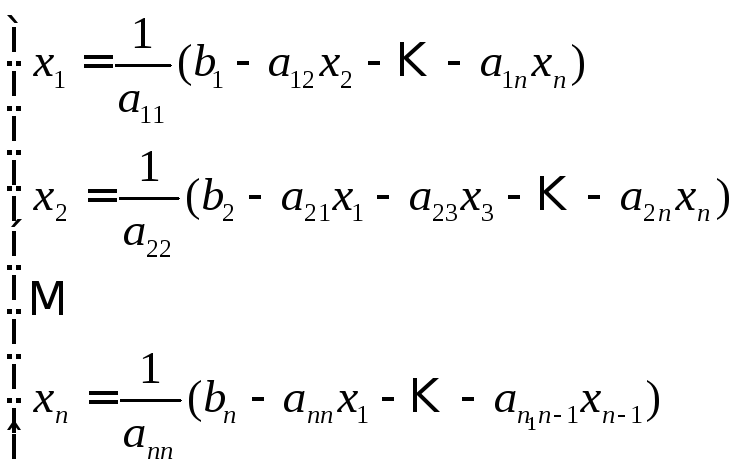 ,
,
а
элементы матрицы С будут:
![]()
При
этом, очевидно, модули диагональных
коэффициентов
![]() матрицы
матрицы![]() больше суммы модулей всех остальных
коэффициентов (не считая свободных
членов) строк этой матрицы, т.е.
больше суммы модулей всех остальных
коэффициентов (не считая свободных
членов) строк этой матрицы, т.е.![]()
![]() .
.
Пример.
Привести к виду, пригодному для метода итерации, систему:
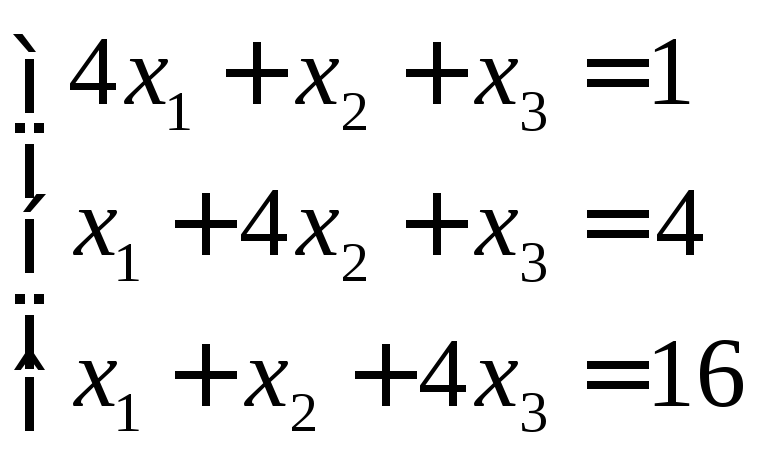
Решение:
В
этой системе
![]() ,
,![]() .
Имеем:
.
Имеем:
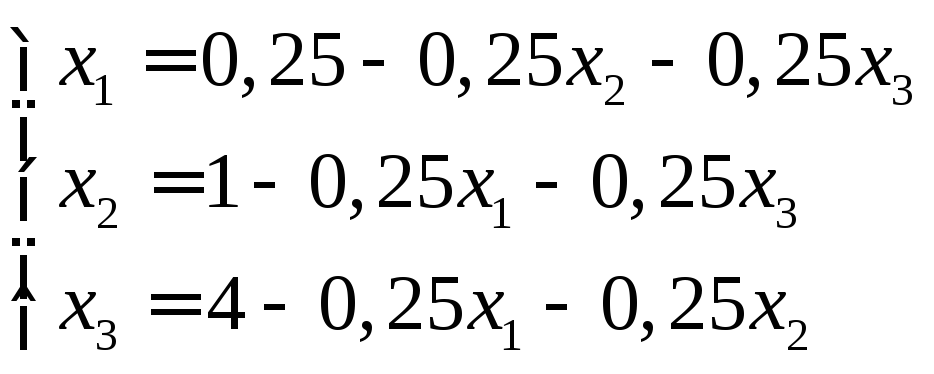
Для
полученной системы выполняются условия
сходимости:
![]()
Пример. Система:
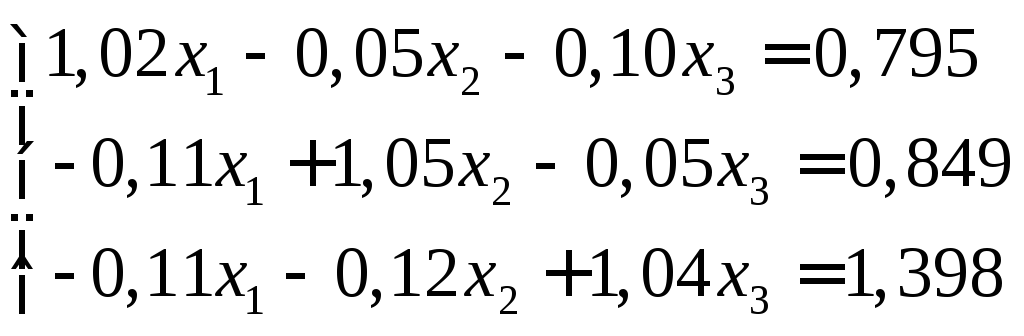
имеет матрицу, в которой диагональные элементы близки единице, а все остальные – значительно меньше единицы. Поэтому для применения метода итерации естественно записать заданную систему в виде:
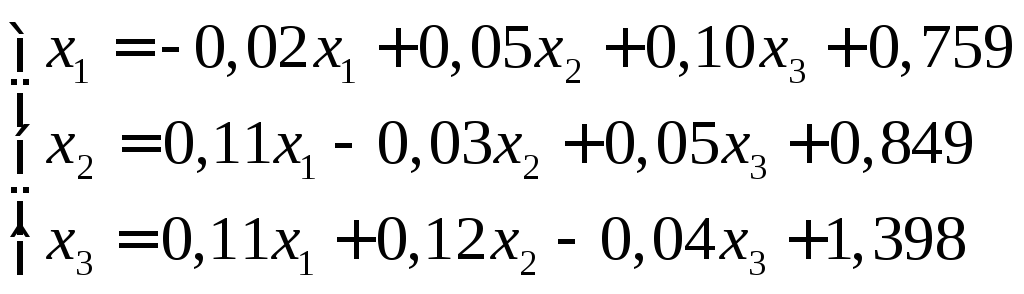
Условия сходимости для полученной системы выполняются, т.к.:
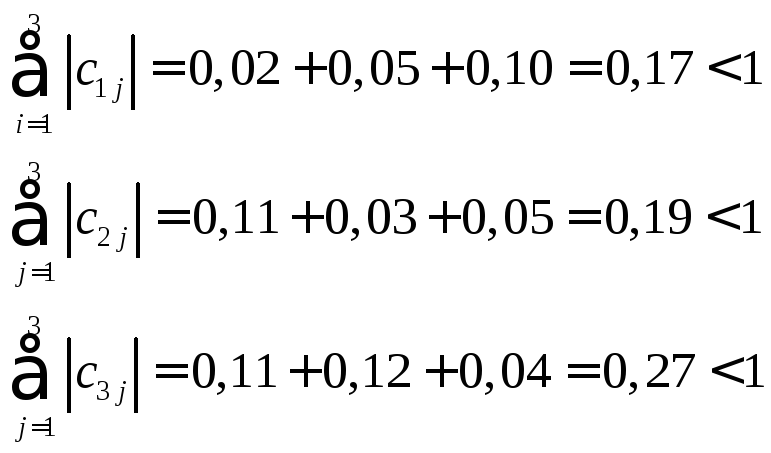
д) Метод Зейделя.
Итерационный метод Зейделя решения линейных систем уравнений представляет собой видоизменение метода простой итерации.
В
этом методе линейная система задается
в виде
![]() ,
а приближения строятся по формулам:
,
а приближения строятся по формулам:
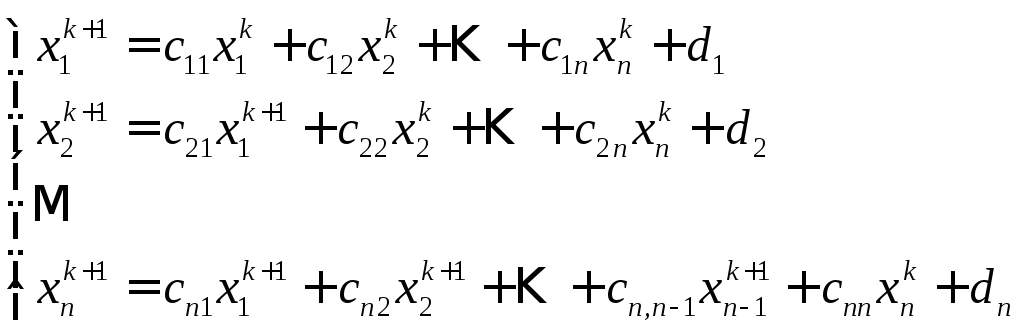
Обычно этот метод дает лучшую сходимость, чем метод простой итерации. При этом условия сходимости остаются верными и для метода Зейделя.
Пример. Методом Зейделя решить систему:
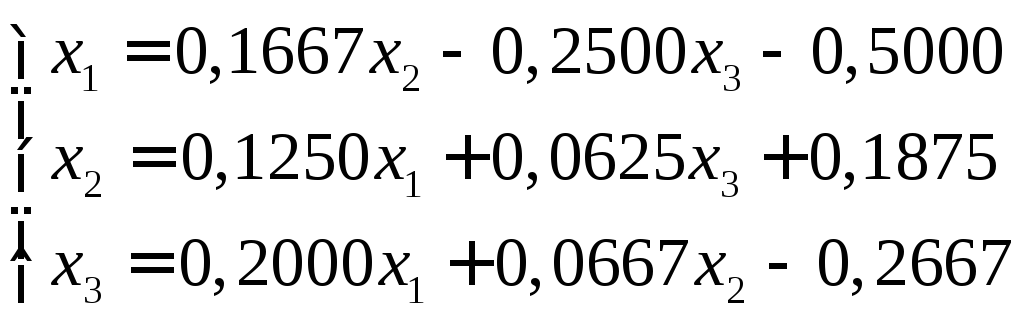
Решение.
Поскольку достаточные условия сходимости итерации процесса выполнены, т.е.: 0,1667+0,2500<1; 0,1250+0,0625<1; 0,2000+0,0667<1, то имеем решение системы.
Последовательные приближения для k=0; k=1:
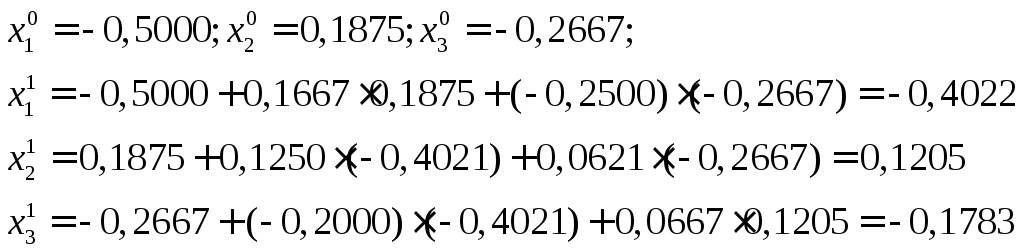
Результаты вычислений сведем в таблицу:
|
Приближенно |
Коэффициенты
при
|
Свободные члены | ||
|
|
|
| ||
|
|
0 |
0,1667 |
-0,2500 |
-0,5000 |
|
|
0,1250 |
0 |
0,0625 |
0,1875 |
|
|
-0,2000 |
0,0667 |
0 |
-0,2667 |
|
|
-0,5000 |
0,1875 |
-0,2667 |
|
|
|
-0,4021 |
0,1205 |
-0,1783 |
|
|
|
-0,4353 |
0,1220 |
-0,1715 |
|
|
|
-0,4368 |
0,1222 |
-0,1711 |
|
|
|
-0,4368 |
0,1222 |
-0,1711 |
|
Таким
образом:
![]()
Численное интегрирование.
Задачей численного интегрирования является нахождение определенного интеграла, если подинтегральная функция задана таблично.
Ниже рассмотрены простейшие формулы приближенного интегрирования (часто называемые квадратурными формулами).
а) Метод прямоугольников.
Этот метод основании
на непосредственном определении
интеграла:
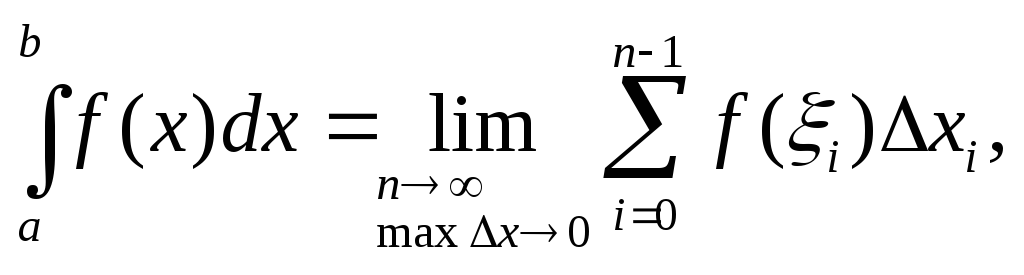 где
где![]() интегральная сумма, соответствующая
некоторому разбиению отрезка
интегральная сумма, соответствующая
некоторому разбиению отрезка![]() и некоторому выбору точек
и некоторому выбору точек![]() на отрезках разбиения.
на отрезках разбиения.
Принимая интегральную
сумму за приближенное значение
определенного интеграла, запишем
квадратные формулы левых
![]() и правых
и правых![]() прямоугольников:
прямоугольников:
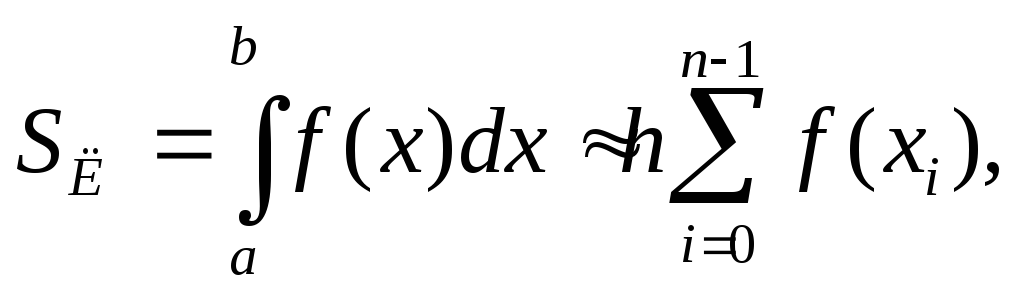
![]() —шаг,
—шаг,
![]() ;
;
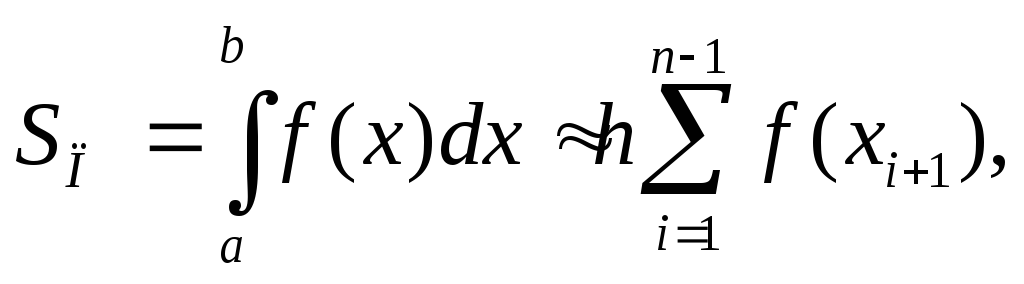
![]() —шаг,
—шаг,
![]() .
.
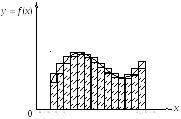
Очевидность этих формул следует из графической интерпретации приближенной площади криволинейной трапеции: ступенчатыми фигурами.
Пример.
С помощью формул левых и правых
прямоугольников вычислить
![]() ,
пологая
,
пологая![]() .
.
Решение.
Точками разбиения служат
![]() а значения подинтегральной функции
а значения подинтегральной функции![]() в этих точка таковы:
в этих точка таковы:
![]()
По формулам левых
и правых прямоугольников численные
значения заданного интеграла равны:
![]() ,
,![]()
Имеем,
![]() .
.
Очевидно, что
увеличение числа разбиений отрезка
![]() дает более точный результат, но при этом
увеличивается и число расчетов. Поэтому
большой интерес представляют квадратурные
формулы, дающие более точный результат
при заданном разбиении отрезка
дает более точный результат, но при этом
увеличивается и число расчетов. Поэтому
большой интерес представляют квадратурные
формулы, дающие более точный результат
при заданном разбиении отрезка![]() .
.
б )
Метод трапеций.
)
Метод трапеций.
В этом случае интегральная сумма
есть среднее арифметическое
формул правых и левых прямоугольников:
![]() (*)Легко
усмотреть геометрический смысл этой
формулы, в которой подинтегральная
функция заменена кусочно-линейной
(говорят в этом случае о линейной
интерполяции дискретной функции. Это
означает, что площадь криволинейной
трапеции
(*)Легко
усмотреть геометрический смысл этой
формулы, в которой подинтегральная
функция заменена кусочно-линейной
(говорят в этом случае о линейной
интерполяции дискретной функции. Это
означает, что площадь криволинейной
трапеции
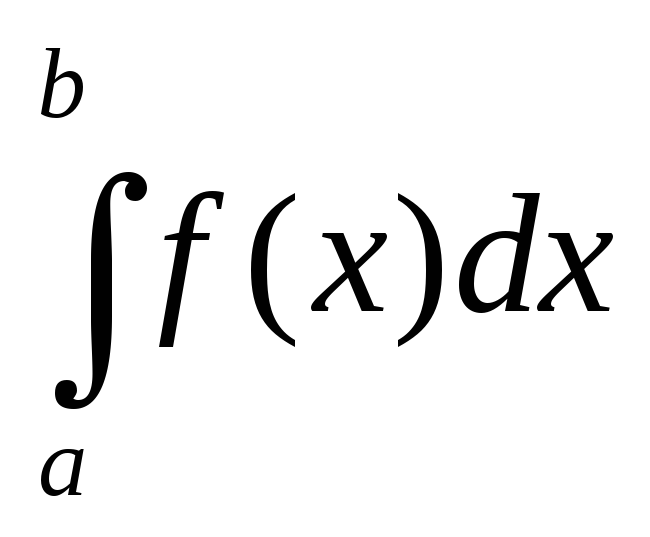 заменяется суммой площадей трапеций
заменяется суммой площадей трапеций![]() .
.
![]() (*)Легко
усмотреть геометрический смысл этой
формулы, в которой подинтегральная
функция заменена кусочно-линейной
(говорят в этом случае о линейной
интерполяции дискретной функции. Это
означает, что площадь криволинейной
трапеции
(*)Легко
усмотреть геометрический смысл этой
формулы, в которой подинтегральная
функция заменена кусочно-линейной
(говорят в этом случае о линейной
интерполяции дискретной функции. Это
означает, что площадь криволинейной
трапеции
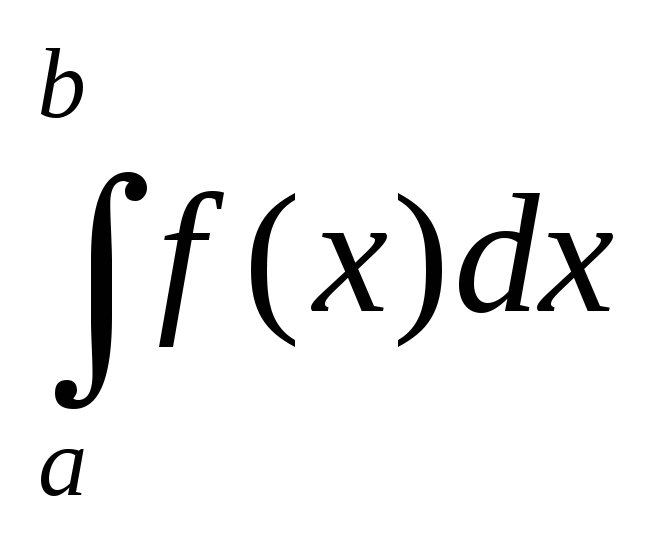 заменяется суммой площадей трапеций
заменяется суммой площадей трапеций![]() .
.
Приведя в формуле (*) подобные члены, окончательно получаем:
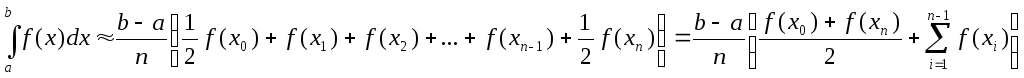 —эту
формулу принято называть общей формулой
трапеций.
—эту
формулу принято называть общей формулой
трапеций.
Пример.
Пользуясь общей формулой трапеций
вычислить
![]()
при
![]() .
.
Решение.
Здесь
![]()
![]() .
.
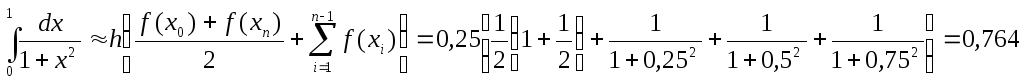
в) Метод Симпсона (метод парабол).
Суть
метода Симпсона заключается
в замене дуги подинтегральной функции
![]() на участке
на участке![]() параболой (т.е. графиком квадратичной
зависимости), проходящей через точки
параболой (т.е. графиком квадратичной
зависимости), проходящей через точки![]() .
.
Имеем:
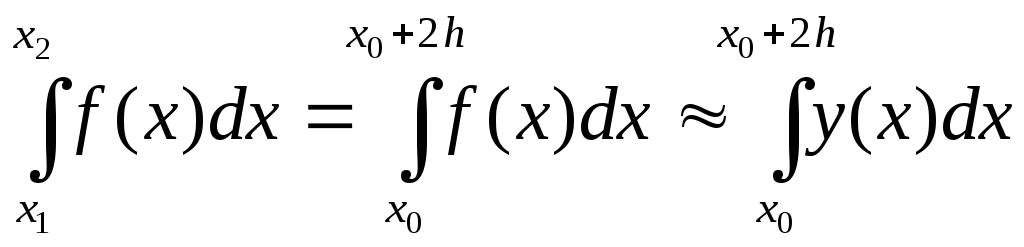 ,
где
,
где![]() —
уравнение параболы.
—
уравнение параболы.
Коэффициенты
![]() определяются из условия прохождения
параболы через точки
определяются из условия прохождения
параболы через точки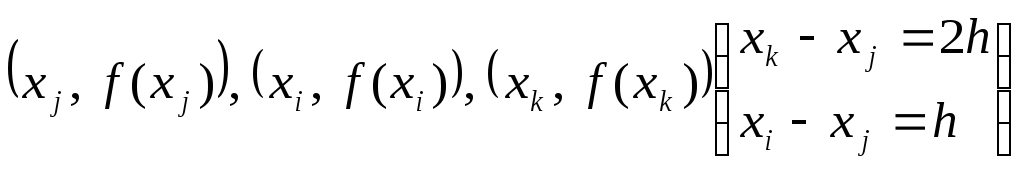
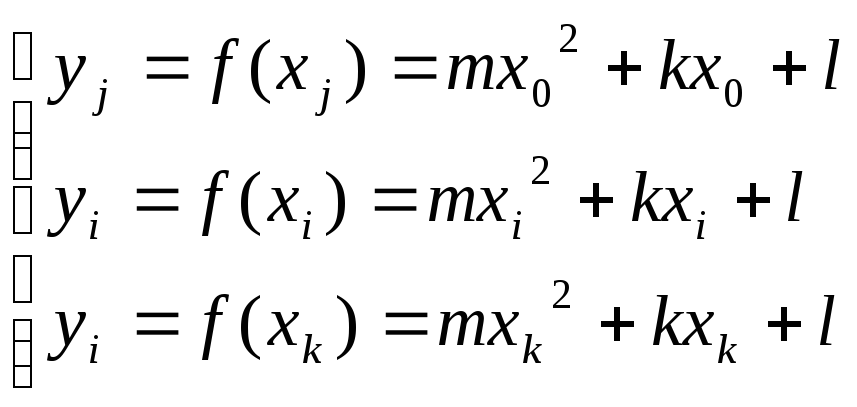
Однако
это приводит к довольно длинным выкладкам:
![]() .
.
Поступим
иначе. Запишем искомую параболу на
отрезке
![]() в виде:
в виде:![]() .
.
Положим
![]() ,
имеем:
,
имеем:
![]() (здесь
(здесь
![]() ).
).
Аналогично:
![]() ,
,
![]() .
.
Отсюда:
![]() .
.
Площадь под параболой есть
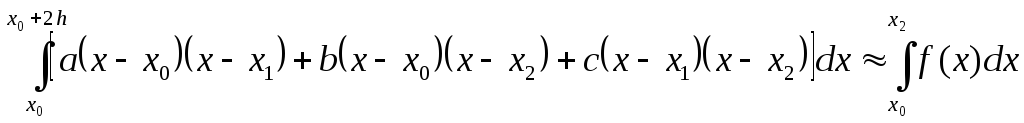 ,
или, учитывая, что
,
или, учитывая, что
![]()
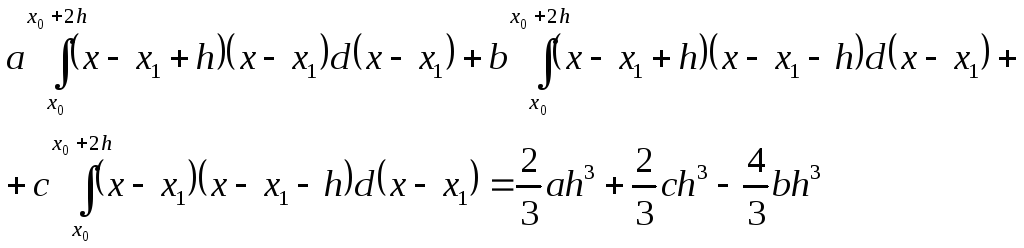
Окончательно:
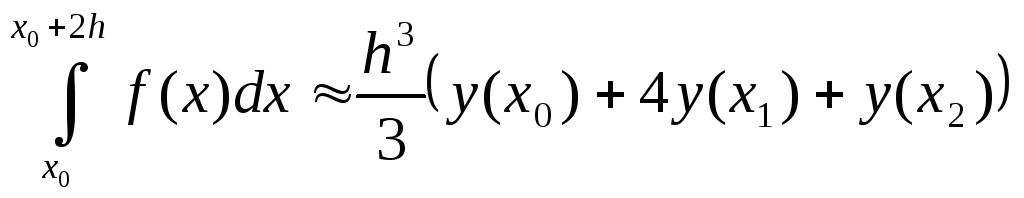 .
.
Таким
же способом можно подсчитать
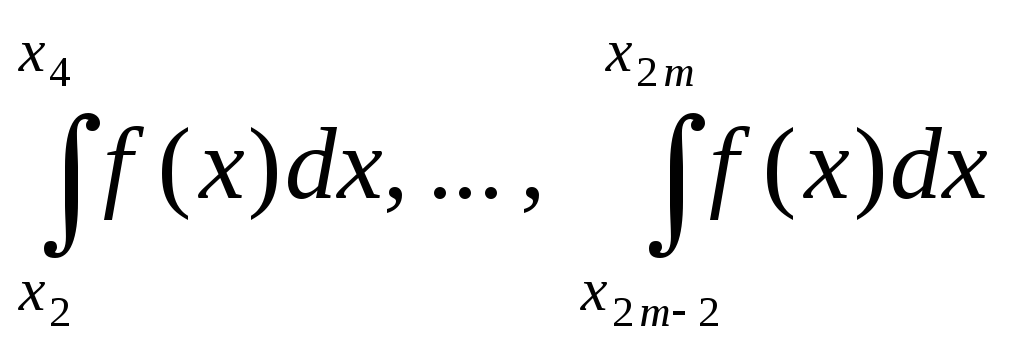 .
.
в) Метод Симпсона (метод парабол).
Суть
метода Симпсона заключается
в замене дуги подинтегральной функции
![]() на участке
на участке![]() параболой (т.е. графиком квадратичной
зависимости), проходящей через точки
параболой (т.е. графиком квадратичной
зависимости), проходящей через точки![]() .
.
Имеем:
 ,
где
,
где![]() —
уравнение параболы.
—
уравнение параболы.
Коэффициенты
![]() определяются из условия прохождения
параболы через точки
определяются из условия прохождения
параболы через точки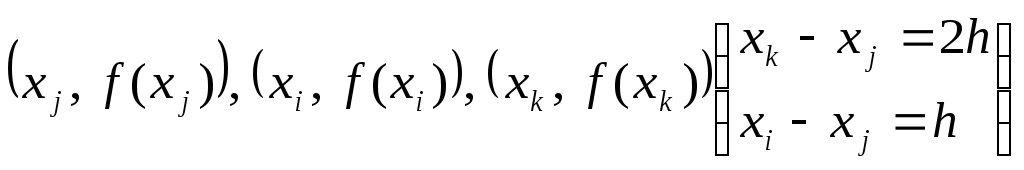
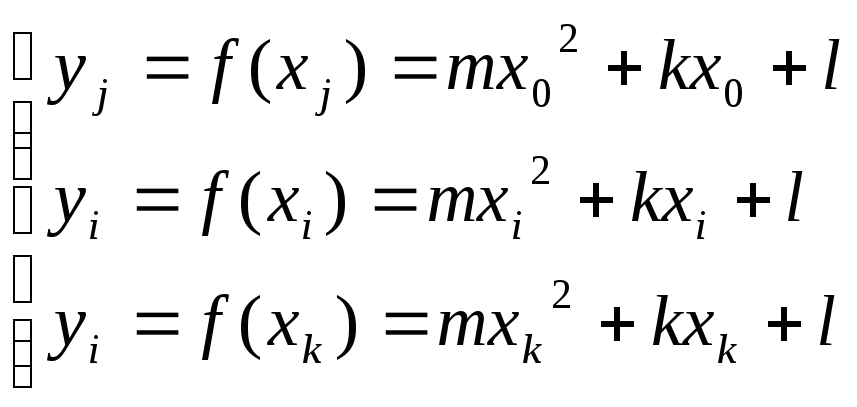
Однако
это приводит к довольно длинным выкладкам:
![]() .
.
Поступим
иначе. Запишем искомую параболу на
отрезке
![]() в виде:
в виде:![]() .
.
Положим
![]() ,
имеем:
,
имеем:
![]() (здесь
(здесь
![]() ).
).
Аналогично:
![]() ,
,
![]() .
.
Отсюда:
![]() .
.
Площадь под параболой есть
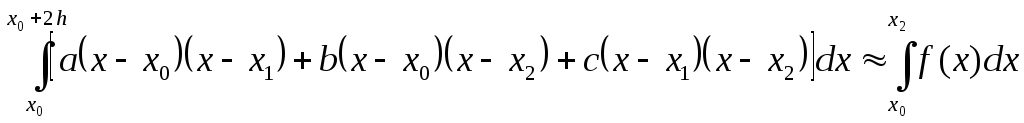 ,
или, учитывая, что
,
или, учитывая, что
![]()
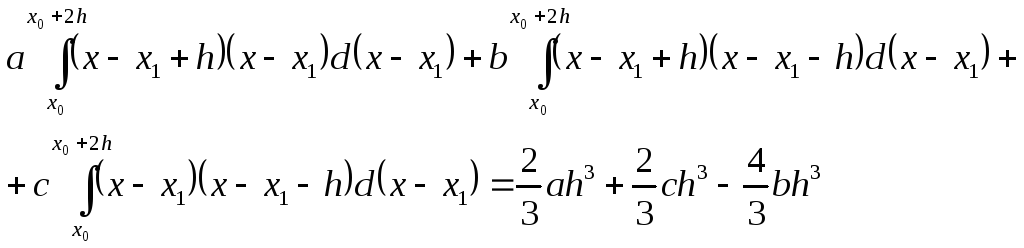
Окончательно:
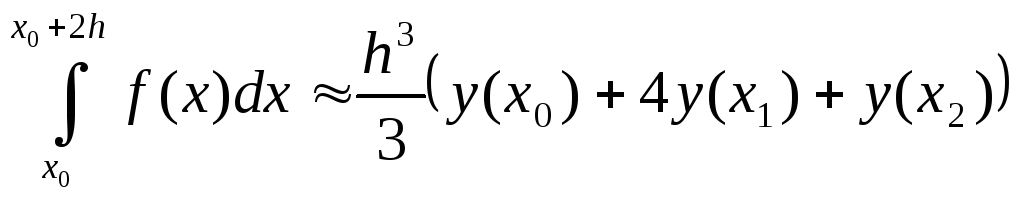 .
.
Таким
же способом можно подсчитать
 .
.
Для
интеграла по всему промежутку
![]() получаем:
получаем:
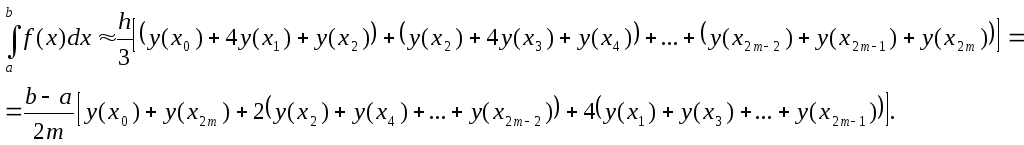
Эта формула называется формулой Симпсона.
Пример.
Найти
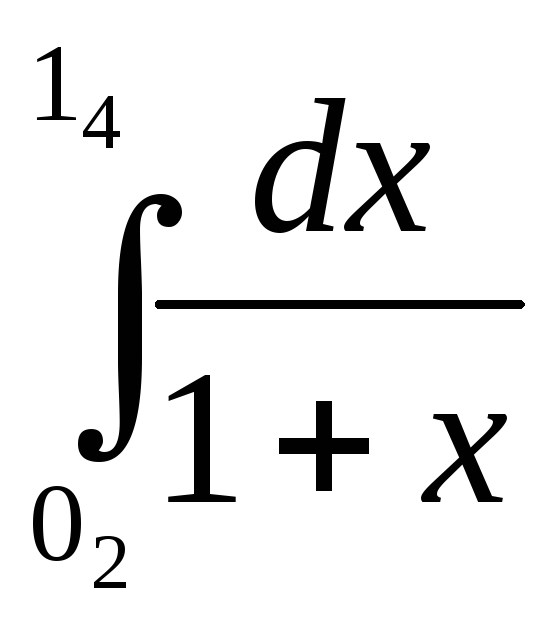 по формуле Симпсона при
по формуле Симпсона при![]() .
.
Решение.
Значения
![]() в точках отрезка:
в точках отрезка:![]() .
.
Формула
Симпсона дает
![]() .
.
Т.к.
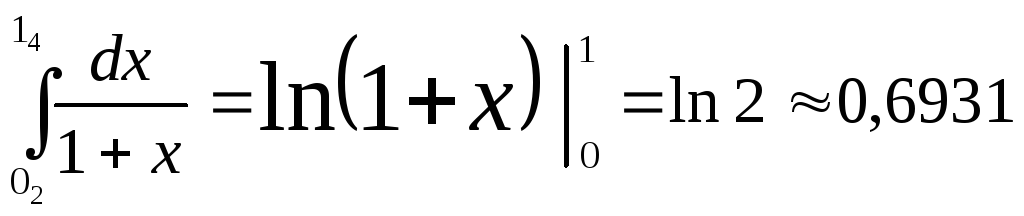 ,
то ошибка
,
то ошибка![]()
(или
![]() ).
).
В то же время ошибка общей формулы трапеций значительно выше:
![]() (или
(или
![]() ).
).
Пример.
Найти
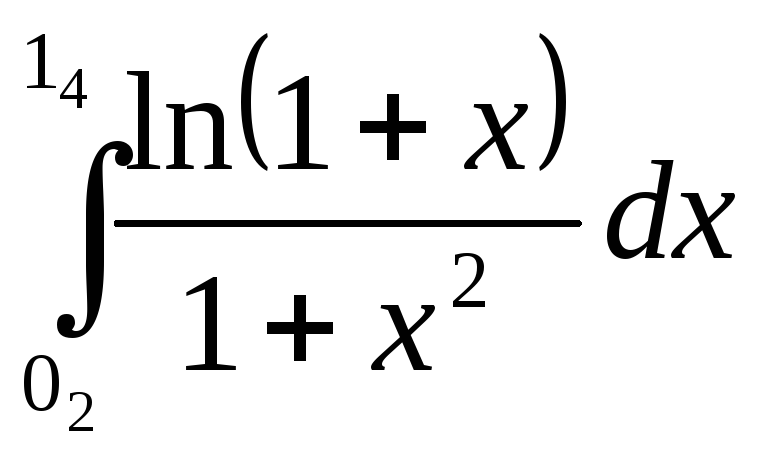 .
.
Решение.
Пусть
![]() .
.
Имеем:
![]() .
.
По формуле трапеции, получаем:
![]() .
.
По формуле Симпсона, получаем:
![]() .
.
Точное
значение
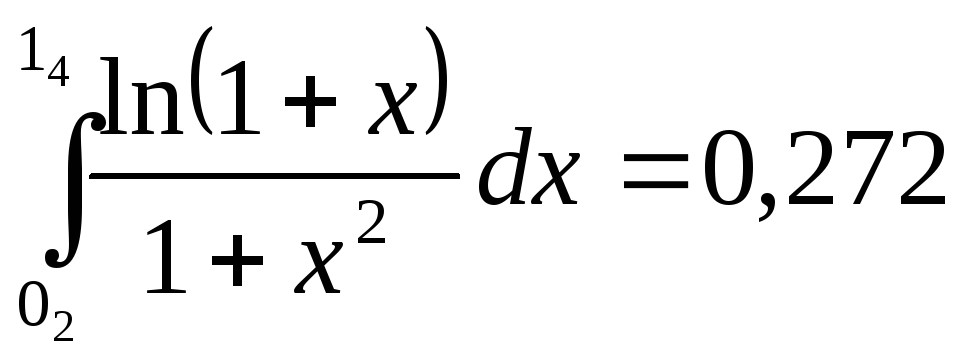 ,
,
а
соответствующие погрешности равны
![]() и
и![]() (или
(или![]() и
и![]() ).
).
Дифференцирование функций, заданных приближенно.
При
вычислении производной функции, заданной
таблицей, следует иметь в виду, что
лучший способ найти
![]() по
двум значениям функции
по
двум значениям функции![]() — это взять такие значения справа и
слева на равном расстоянии от значения
— это взять такие значения справа и
слева на равном расстоянии от значения![]() ,
для которого ищется производная:
,
для которого ищется производная:
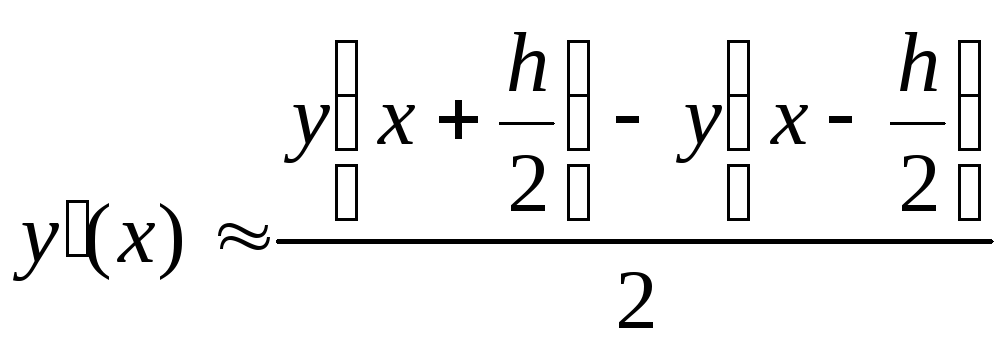 .
.
Аналогично,
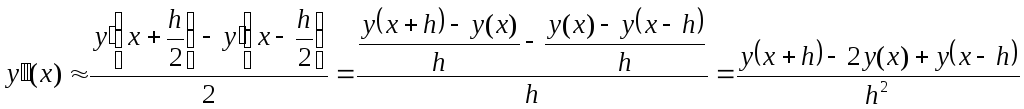 .
.
Пример.
Вычислить значения
![]() и
и![]() ,
если
,
если
![]()
![]() .
.
Решение.
Результаты вычислений
![]() и
и![]() сведем в таблицу:
сведем в таблицу:
-
1,0
1,1
1,2
1,3
1,4
1,5
1,6487
1,733
1,8221
1,9155
2,0138
2,1170
0,846
0,888
0,934
0,983
1,032
0,42
0,46
0,49
0,49
Численное интегрирование дифференциальных уравнений.
Решить
дифференциальное уравнение
![]() численным методом — это значит для
заданной последовательности аргументов
численным методом — это значит для
заданной последовательности аргументов![]() и числа
и числа![]() ,
не определяя функцию
,
не определяя функцию![]() ,
найти такие значения
,
найти такие значения![]() ,
что
,
что![]()
![]() и
и![]() .
.
Очевидно,
что уравнения
![]() ,
как решения
,
как решения![]() при
при![]() ,
должно существовать и быть единственным,
т.е. функция
,
должно существовать и быть единственным,
т.е. функция![]() должна быть непрерывной в рассматриваемой
области по обоим аргументам и иметь
ограниченную частную производную
должна быть непрерывной в рассматриваемой
области по обоим аргументам и иметь
ограниченную частную производную![]() .
.
Излагаемые
ниже методы численного решения
дифференциального уравнения первого
порядка легко переносятся на случай
системы
![]() числа уравнений.
числа уравнений.
а) Метод Эйлера.
Этот
метод состоит в том, что на малом
промежутке
![]() изменения независимой переменной
изменения независимой переменной![]() интегральная кривая дифференцируемого
уравнения
интегральная кривая дифференцируемого
уравнения![]() заменяются отрезком касательной
заменяются отрезком касательной![]() .
.
Отсюда
![]() .
.
(Действительно,
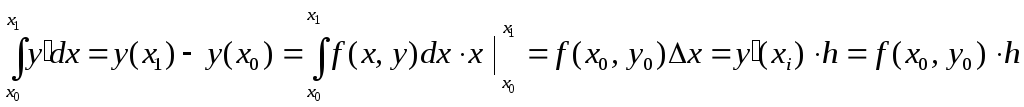 ).
).
Теперь,
принимая точку
![]() за исходную, можно точно таким же методом
получить
за исходную, можно точно таким же методом
получить![]() (здесь число
(здесь число![]() является шагом таблицы).
является шагом таблицы).
Геометрически
интегральная кривая
![]() заменяется ломанной (называемой ломаной
Эйлера).
заменяется ломанной (называемой ломаной
Эйлера).

![]()
Рабочая
формула для определения значений
![]() по методу Эйлера имеет вид:
по методу Эйлера имеет вид:
![]() ,
где
,
где
![]() ,
,![]() ,
,
![]() .
.
Пример.
Применяя метод Эйлера, составить на
отрезке
![]() таблицу значений решения уравнения
таблицу значений решения уравнения![]() с начальным условием
с начальным условием![]() ,
выбрав шаг
,
выбрав шаг![]() .
.
Решение. Результаты вычислений сведем в таблицу:
-
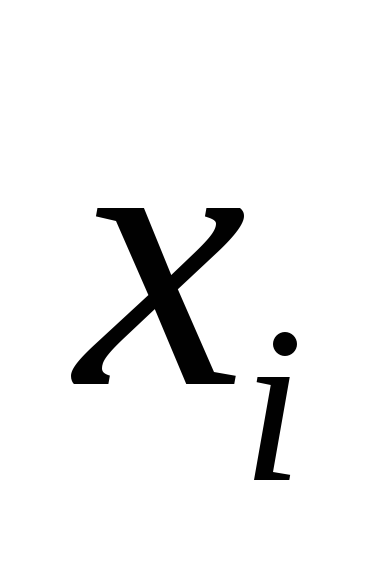
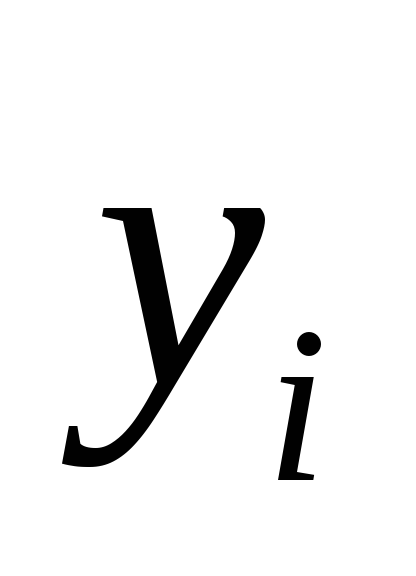
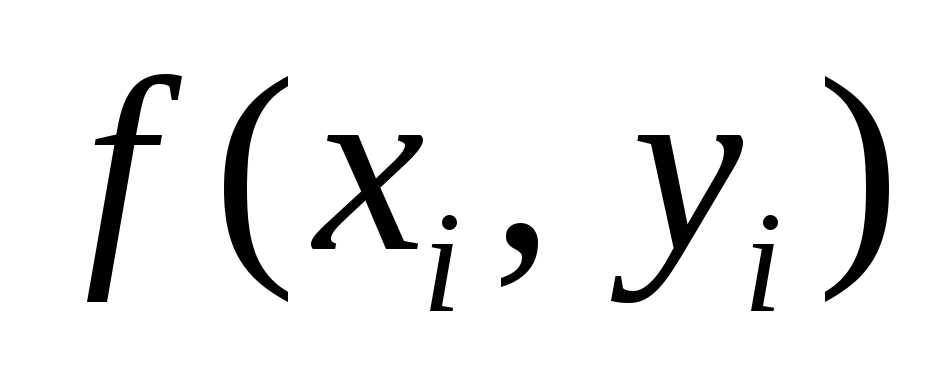
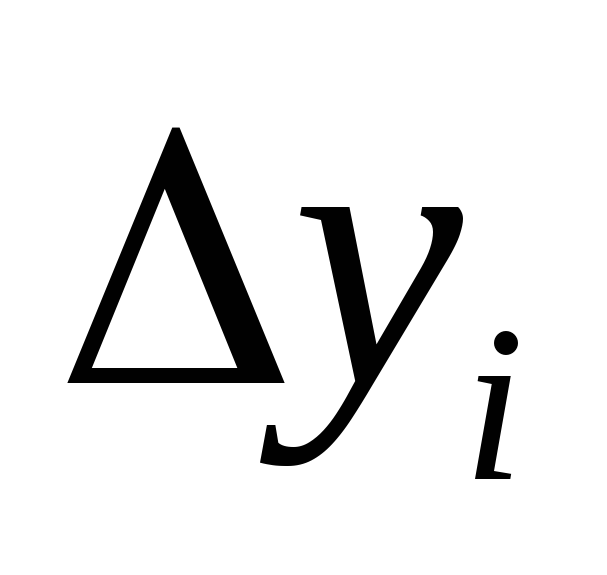
Точное решение
0
1
2
3
4
5
0
0,2
0,4
0,6
0,8
1,0
1,0000
1.2000
1.3733
1.5294
1.6786
1.8237
0
0,3333
0,5928
0,7846
0,9532
1,0000
0,8667
0,7805
0,7458
0,7254
0,2000
0,1733
0,1561
0,1492
0,1451
1,0000
1,1832
1,3416
1,4832
1,6124
1,7320
Из
таблицы следует, что абсолютная
погрешность
![]() ,
а относительная погрешность
,
а относительная погрешность![]() .
.
Решение системы дифференциальных уравнений и дифференциальных уравнений высших порядков методом Эйлера требует их преобразования к системам уравнений 1-го порядка.
Так, для системы
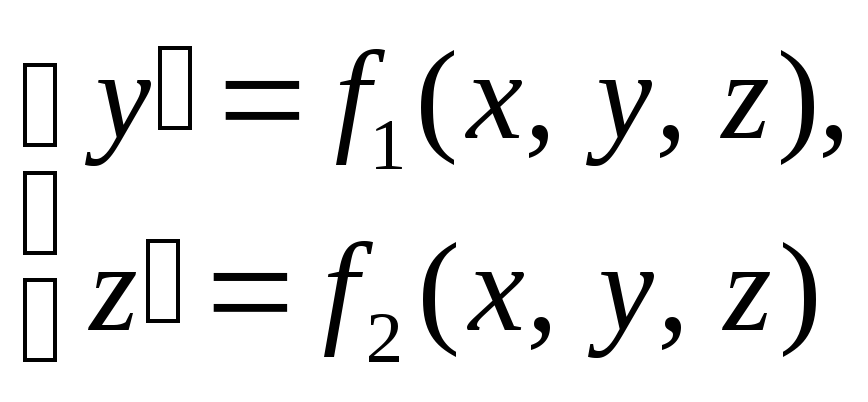
с
начальными условиями
![]() и
и![]() приближенные значения
приближенные значения![]() и
и![]() вычисляются по формулам:
вычисляются по формулам:
![]()
![]() .
.
Пример.
Применяя метод Эйлера, составить на
отрезке
![]() таблицу значений решения уравнения
таблицу значений решения уравнения![]() с начальным условием
с начальным условием![]() ,
выбрав шаг
,
выбрав шаг![]() .
.
Решение.
С помощью подстановок
![]() из заданного уравнения получаем:
из заданного уравнения получаем:
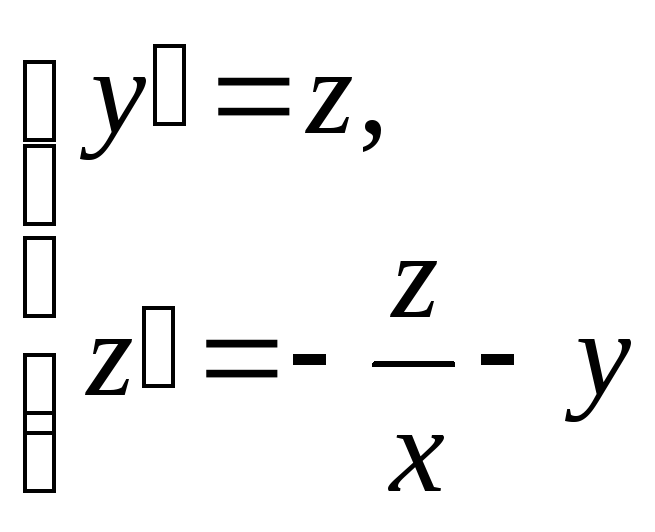
с
начальными условиями
![]() .
.
В полученной системе:
![]() .
.
Вычисления
![]() сведем в таблицу:
сведем в таблицу:
-

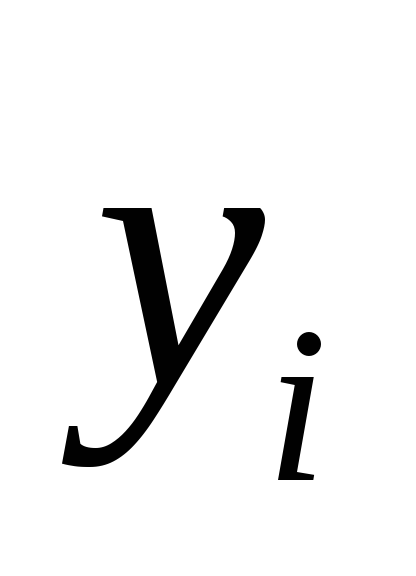
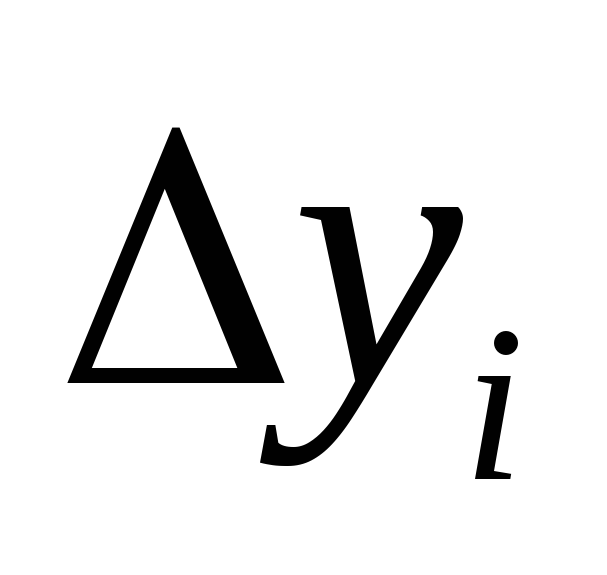
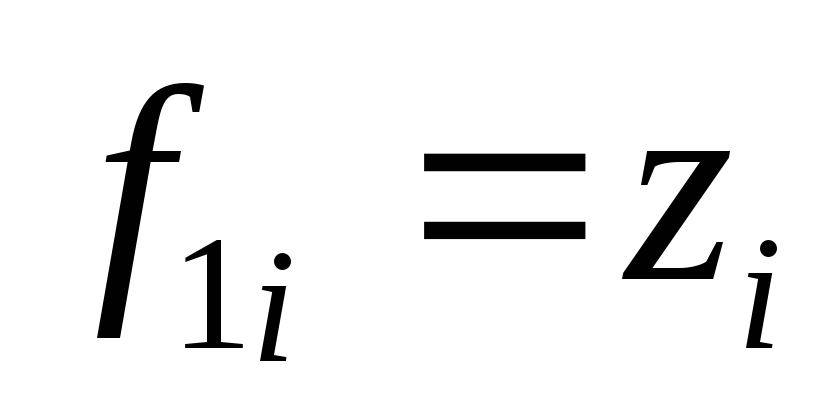
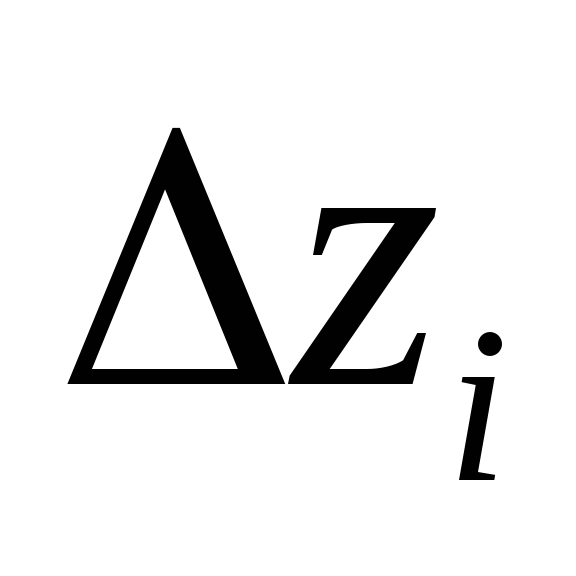
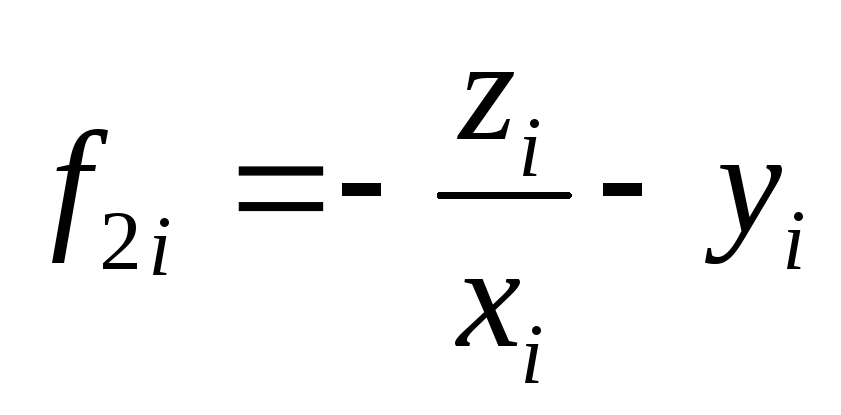
0
1
2
3
4
5
1,000
1,1
1,2
1,3
1,4
1,5
0,77
0.726
0.679
0.629
0.576
0.521
-0,044
-0,047
-0,050
-0,053
-0,055
-0,44
-0,473
-0,503
-0,529
-0,551
-0,033
-0,030
-0,026
-0,022
-0,33
-0,296
-0,260
-0,222
В этой таблице первая строка заполняется так: для того,
что
![]() ;
;![]() ;
;![]() ;
;![]() ,
,
имеем
![]() ;
;
![]() .
.
Используя
формулы
![]() ,
,![]() ,
,
получаем
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таком образом, во второй строке таблицы записываем
![]() ;
;
![]() ;
;![]() ;
;![]() .
По этим значениям находим:
.
По этим значениям находим:
![]() ;
;
![]() ,
,
и, следовательно,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Заполнение
таблицы при
![]() производится аналогично.
производится аналогично.
б) Метод Ронге-Кутта.
Этот метод, имеющий много общего с методом Эйлера, является методом повышенной точности.
Пусть
на отрезке
![]() требуется найти численное решение
уравнения
требуется найти численное решение
уравнения![]() с начальными условиями
с начальными условиями![]() .
.
В
методе Рунге-Кутта, так как и в методе
Эйлера, последовательные значения
![]() искомой функции
искомой функции![]() определяются по формуле
определяются по формуле![]() .
.
Представим
приращение функции
![]() членами до
членами до![]() включительно ряда Тейлора разложения
функции
включительно ряда Тейлора разложения
функции![]() :
:
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() — производные, определяемые последовательным
дифференцированием уравнения
— производные, определяемые последовательным
дифференцированием уравнения![]() .
.
Вместо
непосредственных вычислений приращения
![]() по полученной формуле в методе Рунге-Кутта
определяются четыре числа
по полученной формуле в методе Рунге-Кутта
определяются четыре числа![]() ;
;![]() ;
;![]() ;
;![]() таких,
что:
таких,
что:![]() .Таким
образом, для каждой пары
.Таким
образом, для каждой пары![]() находят
находят![]() и затем
и затем![]() .
.
Вычисления по методу Рунге-Кутта удобно вести по схеме:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
В
столбце 2 и 3 текущей строки записывается
нужное значение
![]() и
и![]() ,
а результаты подставляются в правую
часть уравнения
,
а результаты подставляются в правую
часть уравнения![]() ,
записывается в четвертый столбец той
же строки. В пятом столбце таблицы
получены значения столбца
,
записывается в четвертый столбец той
же строки. В пятом столбце таблицы
получены значения столбца![]() умножаются на шаг интегрирования
умножаются на шаг интегрирования![]() .
Результаты шестого столбца суммируются
и делятся на 6, т.е. определяется
.
Результаты шестого столбца суммируются
и делятся на 6, т.е. определяется![]() и
и![]() .
.
