III.Метод Ньютона (метод касательных)

Пусть корень уравнения отделен на отрезке, причемf’(x) и f’’(x) и сохраняют постоянные знаки на всем отрезке .

Геометрический смысл метода Ньютона состоит в том, что дуга кривой заменяется касательной к этой кривой (отсюда и второе название метода - «метод касательных»).

Рассмотрим два случая:

а) или

Проведем касательную к кривой в точкеB₀ (b,f(b)) и найдем абсциссу точки пересечения касательной с осью Ox. Известно, что уравнение касательной в точке B₀ (b,f(b)) имеет вид:

Поскоку в нашем случае y=0, x=x₁,то получаем: .

Теперь корень уравнения находится на отрезке [a,x₁]. Применяя снова метод Ньютона, проведем касательную к кривой в точке B₁ (x₁,f(x₁)) получим: , и вообще:. Очевидно, что каждый следующий член последовательностиесть более близкое приближенное значение к корню, чем предыдущий. Однако всев этом случае остаются больше истинного значения корня, т.е.- приближенное значение корняс избытком.

б)Пусть или, т.е.

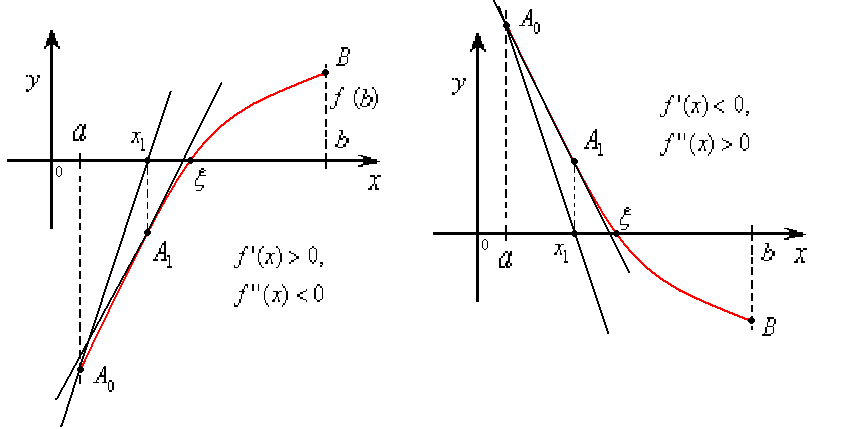
Если снова провести касательную к кривой в точкеB_, то она пересечет ось абсцисс в точке, не принадлежащей отрезку . Потому проведем касательную в точкеA₀(a,f(a)) и запишем ее уравнение

Поскоку y=0, x=x₁,то получаем: .

Очевидно, корень находится на отрезке [x₁,b]. Повторив процедуру в точке A₁ (x₁,f(x₁)), получаем: и вообще.

Итак, получив последовательность приближенных значений искомого корня, отметим, что каждый последующий член ее ближе к истинному корню, чем предыдущий. Отсюда следует, что- приближенное значение корняс недостатком.

Анализ полученных формул в случае а) и в случае б) приводит к следующему правилу выбора начального приближения корня:

-за исходную точку следует брать тот конец отрезка, в котором знак функциисовпадает со знаком второй производнойf’’(x). Очевидно, в первом случае (случае а)) и начальная точка, а во втором случаеи начальное приближение есть.

Примечание

1. Для оценки погрешности приближенного значения корня 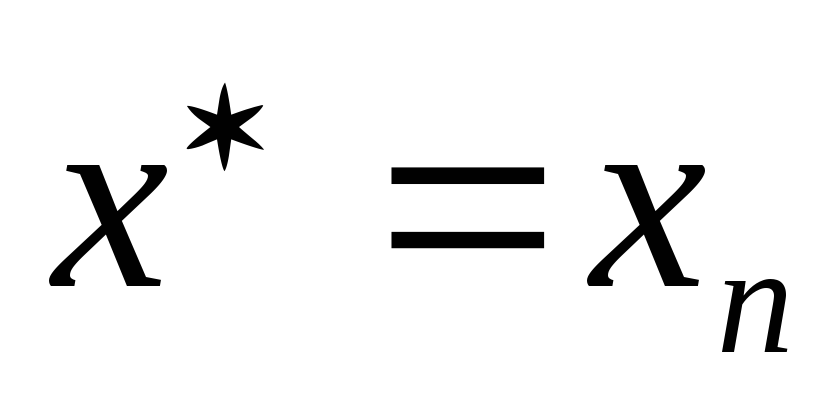будем пользоваться формулой:, где(эта формула используется в методе хорд).

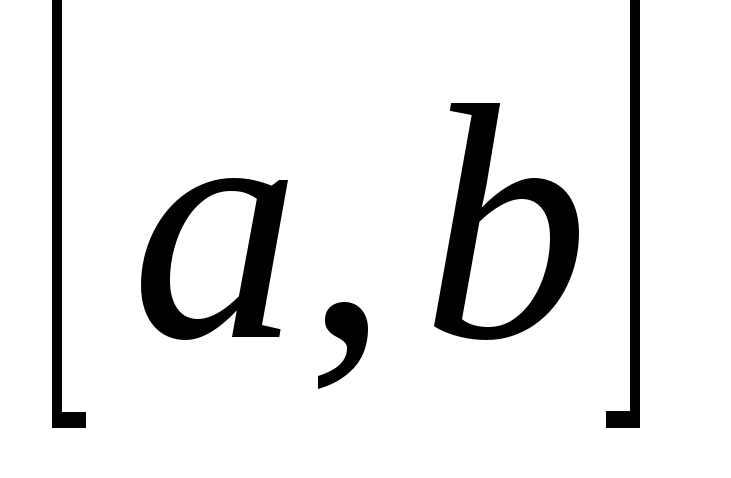2. В том случае, когда отрезок настолько мал, что на нем выполняется условие, где, точность приближения наn-ом шаге оценивается следующим образом: если .

3. Если производная f’(x) мало меняется на отрезке 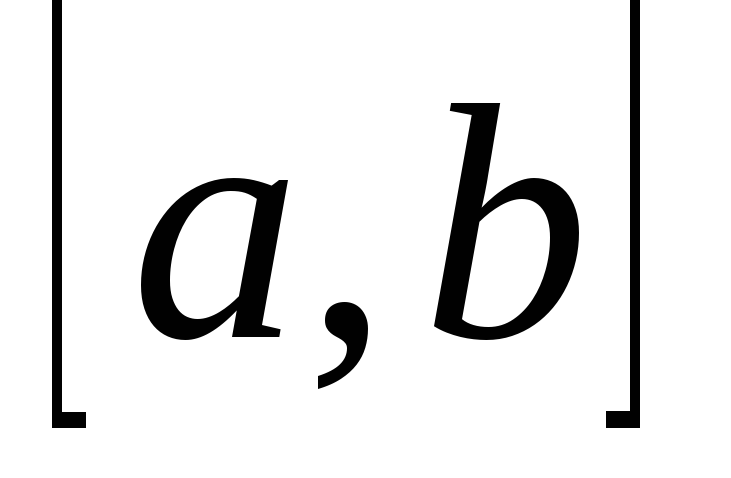, то для упрощения вычислений можно пользоваться формулой:, т.е. значение производной в начальной точке достаточно вычислить только один раз. Геометрически это означает, что касательные в точкеB_n (x_n,f(x_n)) заменяются прямыми, параллельными касательной, проведенной к кривой в точкеB₀(x₀,f(x₀)).

Пример

Методом касательных уточнить до корень уравнения, расположенный на отрезке [-2,75;-2,5] .

Решение

Имеем : f(-2,75)=-2,75³+3*2,75²-3<0, f’’(x)=6x+6<0, , т.е..

Это означает, что вычисления надо вести по формуле . Находим:f’(x)=3x²+6x, f’(x₀)=f’(-2,75)=(-3)*2,75*(-2,75+2)=6,1875.

Для удобства все вычисленное сведем в таблицу:

n	xn			3	f(xn)
0	-2,75	-20,797	7,5625	22,6895	-1,111	0,179
1	-2,571	-16,994	6,6100	19,8300	-0,164	0,026
2	-2,545	-16,484	6,4770	19,431	-0,053	0,008
3	-2,537	-16,329	6,4364	19,309	0,020	0,003
4	-2,534	-16,271	6,4212	19,2636	0,007	0,001
5	-2,533

Из этой таблицы следует, что и поэтому корень.

Пример

Методом касательных уточнить до корень уравнения, расположенный на отрезке [0,982;1,178].

Решение

Здесь a=0,982; b=1,178, находим f’(x)=1-cos x; . f’’(x)=sinx>0 на [0,982;1,178], . Значит,

Вычисления будем вести по формуле . Результаты вычислений сведем в таблицу:

n	xn	-sin xn
0	1,178	-0,92384	0,00416	0,61723	-0,0065
1	1,1715	-0,92133	0,00017	0,01123	-0,0002
2	1,1713	-0,92127	0,00003	0,61110	-0,00005
3	1,17125

Из таблицы видно, что . Таким образом,.