2.Метод Лагранжа.

Если - верхняя граница положительных корней функции,- верхняя граница положительных коней,-верхняя граница положительных корней,-верхняя граница положительных корней, то все отличные от нуля действительные корни уравнения(если они существуют) лежат внутри интервалов.

При этом: если коэффициенты полинома удовлетворяют условию, то верхняя граница положительных корней уравнениянаходится по формуле:, гдеm- номер первого отрицательного коэффициента ;B- наибольший по модулю отрицательный коэффициент уравнения .

Пример: Методом Лагранжа определить границы корней уравнения:

Решение: Здесь

Следовательно,

Для полинома:

и поэтому:

Для многочлена: имеем

и значит

Наконец, для полинома

Имеем:

Поэтому,

Итак, корни исходного уравнения лежат в интервалах (-2;-1/3.828) и (1/33;3)

3.Метод Ньютона.

Если при х = с полином и все его производные принимают положительные значения, то «с» является верхней границей положительных корней уравнения=0.

Пример: Определить верхнюю границу положительных корней уравнения методом Ньютона.

Решение: Проверке подлежат только c=x>0.

Пусть с=1, тогда

Дальнейшая проверка для с=1 не нужна.

Пусть с=2, тогда . Таким образом верхней границей положительных корней является число 2, то естьR=2.

Пример: Определить верхнюю границу положительных корней уравнения методом Ньютона.

Решение: Проверке подлежат только с=х>0. Пусть с=1, тогда

Дальнейшая проверка для с=1 не нужна.

Пусть с=2, тогда , .

Таким образом, верхней границей положительных корней является число 2, то есть R=2.

Графические методы решения уравнений и систем

Графический метод решения конечных уравнений с одной переменной - один из приближенных методов, позволяющий выбрать первое приближение, с которого начинается уточнение решения уравнения.

Выделяют два способа графического решения уравнения:

В первом способе все члены уравнения переносят в левую часть, то есть представляют его в виде. После этого строят график функции, где- левая часть уравнения. Абсциссы точек пересечения графика функциис осью Ох и являются корнями уравнения, так как в этих точках у=0:

y

x

Во втором способе все члены уравнения разбивают на две группы: одну из них записывают в левой части уравнения, а другую - в правой, то есть представляют его в виде . После этого строят графики двух функцийи. Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения.

Так

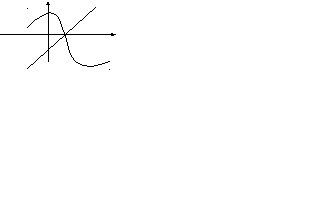y

x

Из равенства следует, что- корень уравнения.

Пример: Решить графически уравнение:

Решение: Согласно первому способу решения уравнения строим график функции

y

1 x

-1

Абсцисса точек пересечения этого графика с осью Ох равна 1. Это означает, что заданное алгебраическое уравнение имеет один действительный корень х=1 (два других корня - комплексные)

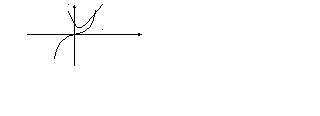
Согласно второму способу заданное уравнение можно переписать в виде: и построить графики функцийи. Абсцисса точек пересечения этих графиков х=1

y

1 x

Пример: Найти графическим способом корни трансцендентного уравнения:

Решение: Перепишем это уравнение в виде . Так как функция левой и правой частей уравнения имеют общую область определения (интервал 0<x<+∞), то будем искать корни в интервале ]0,+ ∞[.

Построив графики функций и

y

1 x

Находим корни уравнения: прямая пересекает в двух точках с абсциссами 0,00001 и1,75.

Пример: Найти графически корни трансцендентного уравнения

Решение: Строим функции и

y

1 2

Корнями уравнения являются абсциссы точек пересечения графиков, то есть =1,=2

Графические методы решения систем уравнений

Рассмотрим на примере системы двух нелинейных уравнений с двумя переменными. При этом если в заданной системе:

Оба уравнения можно разрешить относительно одной из двух переменных, то система может принять вид:

то есть получаем уравнение: .

В общем же случае строят кривые и, и находят их точки пересечения.

Пример: Считая x>0 , найти графически решения системы уравнений:

Решение: Разрешив заданные уравнения относительно y, то есть

, ,

получим уравнение .

Строим графикии:

Y

-0.28 1 x

Абсцисса и ордината точек пересечения графиков этих функций есть решение заданной системы, то есть х=1,22; у=-0,28

Пример:Найти графически решения системы уравнений:

Решение: Перепишем заданную систему в виде:

Здесь первое уравнение задает эллипс, а второе-гиперболу:

y

x

Эти кривые второго порядка пересекаются в двух точках =0,55 ;=-0,46;=1,7;=1,6.

Отделение корней конечных уравнений.

Отделить корни уравнения – это значит разбить всю его область допустимых значений на отрезки, в каждом из которых содержится один корень. Итак, корень уравненияне имеет других корней.

Отделение корней является первым шагом в нахождении приближенных значений корней уравнения с заданной степенью точности. Этот шаг может проводиться как графически, так и аналитически.

Аналитические методы отделения корней уравнения строятся на базе математического анализа функций.

Примечание:

1. Если кривая к-раз пересекает ось абсцисс, то функция имеетк простых корня. Так если график функции имеет вид

y