Элементарная теория погрешностей

Структура погрешности

В результате численного решения задачи существуют четыре источника погрешностей:

• Математическая модель задачи;

• Исходные данные;

• Вычислительный алгоритм;

• Округление исходных данных, промежуточных или окончательных результатов.

Первые два источника погрешностей к неустранимой погрешности решаемой задачи. Третий источник порождает остаточные погрешности как результат замены бесконечных процессов конечной последовательности действий. Так если в ряде sinx = x - . взять определенное количество членов и принять их сумму за sinx, то, естественно, допускается погрешность.

Четвертый источник обуславливает зарождающиеся погрешности при отбрасывании младших разрядов числа. Так, если разрядная сетка ЭВМ допускает запись семизначных десятичных чисел, то записью числа 0,9835478932 в ячейке будет округленное число 0, 9835479.

Примечание Приведенные погрешности, чаще в увеличенном размере, переходят в результаты вычислений.

Оценка погрешности

Оценка погрешности может быть осуществлена с помощью: абсолютной погрешности, относительной погрешности, остаточного члена, статистических оценок.

Пусть а – точное, вообще говоря, неизвестное числовое значение некоторой величины, а a* - известное приближенное значение этой величины. Тогда число ∆(а*) = │а – а*│ есть истинная абсолютная погрешность числа а*.

Величину δ(а*) = ∆(а*)/│а*│ называют истинной относительной погрешностью приближенного числа а*.

Очевидно, что если а неизвестно, то неизвестны и ∆(а*) и δ(а*). Именно, в этом случае целесообразно применение граничных величин истинных погрешностей: │а – а*│ ≤ ∆*(а*), δ(а*) ≤ δ*(а*).

Основные теоремы о представлении чисел в позиционной системе счисления

1. Каждое число, представленное в позиционной системе счисления конечной последовательности цифр, является рациональным числом.

Пример

2∙10¹ + 3∙10⁰ + 0∙10^-1 + 4∙10^-2 + 0∙10^-3 = 23,040 = 567/25 (25, 567 € N) – десятичная система счисления.

Пример

1∙2¹ + 0∙2⁰ + 0∙2^-1 + 1∙2^-2 + 1∙2^-3 = 10,011 – двоичная система счисления.

Очевидно, что запись числа 10,011 в десятичной системе есть 2,375. Действительно 2∙10⁰ + 3∙10^-1 + 7∙10^-2 + 5∙10^-3 = 2,375

2. В каждой позиционной системе можно представить точно только некоторое подмножество рациональных чисел (зависящее от основания q).

Пример

Числа 1/3, 1/7, 1/9, 1/11, 1/13, 1/17, 1/19, … нельзя представить в десятичной системе счисления в виде конечной последовательности цифр.

Пример

Число 1/25 в десятичной системе счисления записывается как 0,004, а в двоичной (троичной, четверичной, шестиричной, семиричной, и т.д.) 1/25 конечной последовательностью цифр представлено быть не может.

3. Рациональное число x/y (x€Z, y€Z, x,y – взаимно простые) может быть точно представлено в позиционной системе с основанием q тогда и только тогда, когда каждый простой множитель в разложении числа y является простым множителем в разложении q.

Пример

В десятичной системе счисления, т.е. когда q = 10, представимы только такие рациональные числа x/y € Q = { r € D: r = x/y, y € N, x, y – взаимно простые }, у которых у содержит лишь простые множители 2 и 5.

В этом плане: ½ = 0,5; 1/5 = 0,2; 1/8 = 0,25; 1/25 = 0,04; 19/8 = 2,375; 7/16 = 0,4375; 3/200 = 0,015.

Итак, поскольку не каждое рациональное число (и тем более не каждое действительное) число можно представить в позиционной системе в виде конечной цифровой последовательности, то приходится применять приближенные значения представляемого числа, содержащие ограниченное число цифр. К этому прибегают и тогда, когда точное число содержит конечное, но слишком большое число цифр.

Запись действительных чисел в ЭВМ

Современные ЭВМ оперируют с числами, записанными либо в форме с фиксированной запятой, либо в форме с плавающей запятой.

В первой записи все числа имеют модуль, меньший 1, а число цифр после запятой – фиксировано, т.е. машина оперирует с числом х!

Х = sign x ∑ (i=1 по k) α_i q^-i => sign x (α₁, α₂ ,…α_k),

Где q – основание системы счисления, α_i - цифра, 0≤α_i≤q; sign x – знак числа, т.е. sign x € {+,-}.

Наибольшее распространение получила вторая запись числа – запись с плавающей запятой:

X = sign x q^Px ∑ (i=1 по k) α_i q^-i = ± q^Px M_x

Здесь М_х - мантисса числа, т.е. М_х = (α₁, α₂ ,…α_k), P_x – порядок числа, k – число разрядов.

Если α₁ мантиссы М_х не равно 0, то число х называется нормализованным.

Пример

Число 821,26 в нормализованном виде представляется как х = 0,82126∙10³ (здесь q=10, M_x = 0,82126, p=3)

Пример

Двоичное число 1101,01 в нормализованном виде есть число х = 0,110101∙2⁴

Приближенные значения числа

Цифры, составляющие приближенное число, могут быть значащими, верными и сомнительными.

- Верной (точной) цифрой называется цифра, погрешность которой не превышает половины единицы следующего разряда, т.е. если ∆*(а*)≤0,5∙10^m-1+n (где m – число разрядов а*, n – число верных цифр в нем).

Пример

Число 3,142 является приближенным значением числа π с четырьмя точными (верными) значащими цифрами, т.к.:

│π – 3,142│ = │3,14159… - 3,142│< 0,0005 = 0,5∙10³

- Значащими цифрами числа а ≈ а* = <α_n,… α₁, α₀, α_-1, α_-2,…, α_-m> называются все его цифры, кроме 0, стоящих левее первой отличной от 0 цифры (если приближенное число – десятичная дробь), и нулей, стоящих в округленных разрядах (если это число - целое).

Пример

В числах:

54,297 – пять значащих цифр,

0,000704 – три значащих цифры,

1,90007 – шесть значащих цифр.

Пример

Число 0,020, являющееся приближенным значением числа 0,02035, имеет три десятичных знака (разряда), а значащих цифр – две (2 и следующий за ней 0). Нуль в конце числа 0,020 есть значащая цифра, показывающая, что число 0,02035 оборвано (округлено) до третьего десятичного знака, а поэтому не писать его нельзя. Нули, стоящие слева от цифры 2, не являются значащими цифрами.

Очевидно, что значащая цифра α_t является верной, если ∆(а*)≤0,5q^t (здесь q – основание системы счисления действительного числа а*).

- Сомнительной цифрой числа называется цифра, следующая за верной (точкой).

Пример

Приближенным значением числа а = √19 (=4,358898…) возьмем среднее арифметическое приближенных чисел а₁* = 4,32 и а₂* = 4,37 (соответственно с недостатком и избытком, т.е. а₁*<a<a₂*) :

а* = (4,32 + 4,37)/2 = 4,345

В этом приближенном числе 4,345 с четырьмя значащими цифрами первые две цифры верные (4 и 3), а третья и четвертая – сомнительные.

Замечание

- Число называется приближенным с недостачей, если оно меньше точного числа (т.е. а*<a).

Пример

Число 3,14 есть приближенное числа π = 3,14159265… с недостачей.

- Число называется приближенным с избытком, если оно больше точного числа (т.е. a*>a).

Пример

Число 0,699 есть приближение с избытком числа lg5 = ,698970…

- На числовой оси каждому точному числу соответствует одно единственная точка, а приближенному числу – интервал.

Пример

если 3 – точное число, то ему соответствует точка с координатой 3, а если 3 – приближенное число, то ему соответствует интервал допустимых значений 2,50000… - 3,49999… (т.к. округляя эти числа, получается приближенное число 3). Очевидно, что чем больше в числе верных десятичных знаков, тем меньше интервал неопределенности. Так, на числовой оси для приближенного числа 3,0 соответствует интервал 2,95000… - 3,049999… .

Округление чисел

В приближенных вычислениях часто приходится округлять числа как приближенные, так и точные, т.е. отбрасывать одну или несколько последних цифр и при необходимости заменять их другой цифрой.

Для уменьшения погрешности округления чисел приняты правила округления (по дополнению), которые согласуются с принципом А.Н. Крылова:

«Приближенное число следует писать так, чтобы в нем все значащие цифры, кроме последней, были верными, и лишь последняя цифра была сомнительной, и притом не более как на 1-2 единицы».

Пример

Пусть число 29832732 получено в результате приближенных вычислений и пусть четвертая цифра в этом числе сомнительная.

Округленное число в этом случае будет записано как 2,983∙10⁷.

Итак, при округлении чисел следует придерживаться правила дополнения:

- если первая слева из отбрасываемых цифр больше или равна 5, то все отбрасываемые цифры заменяют дополнительной единицей младшего сохраняемого разряда; если же первая из отбрасываемых цифр меньше 5, то все отбрасываемые цифры не изменяют последней сохраняемой цифры приближенного числа.

Пример

Округлением числа 2,4627 до тысячных, сотых и десятых долей являются соответственно следующие приближенные числа: 2,463; 2,46; 2,5.

Пример

Округлить число 7203654 до десятков, сотен, тысяч и десятков тысяч.

Имеем соответствующие приближенные числа: 7203650; 7203700; 7204000; 7200000 или 720365∙10; 72037∙10²; 7204∙10³; 720∙10⁴ (последняя форма записи приближенных чисел указывает число округленных разрядов точного числа).

Замечание

1. Правила округления построены таким образом, чтобы абсолютная погрешность, возникающая при округлении, не превышала пяти единиц первого отброшенного разряда.

2. Округляют числа или до определенного десятичного знака (разряда), или до определенного количества значащих цифр.

Пример

Округлить число 0,07025 до третьего десятичного знака (тысячных долей).

Имеем а = 0,07025 (здесь четыре значащих цифры – 7, 0, 2, 5), а* = 0,070 (здесь 7, 0 – значащие цифры).

Пример

Округлить числа 4576681 и 499971 до четырех значащих цифр.

Имеем а₁ = 4576681, а₁* = 4577∙10³,

а₂ = 499971, а₂* = 5000∙10².

Отметим, что при округлении приближенного числа а* получаем новое приближенное число (а*)*, абсолютная погрешность которого складывается из абсолютной погрешности а* и погрешности округления последнего.

Пример

Округлить сомнительные цифры числа а* = 34,124 ± 0,021. Определить абсолютную погрешность результата.

Решение

Приближенное число а* имеет три верные цифры – 3, 4, 1, т.к. а* - 0,021<а<а* + 0,021, или 34,103<a<34,145 и, очевидно, ∆(а*) = 0,021<0,05. Следовательно, последние две цифры а* 2 и 4 – сомнительные. Округлив а*, имеем (а*)* = 34,1.

Суммарная погрешность ∆(а*)* = ∆(а*) + ∆ (окр а*) = 0,021 + 0,024 = 0,045<0,05 итак, все значащие цифры числа (а*)* верные, т.е. (а*)* = 34,1.

Пример

Округлить сомнительные цифры приближенного числа а* = 36,7245 ± 0,0026, оставив верные разряды. Определить абсолютную погрешность результата.

Решение

По условию 36,7245 – 0,0026<a<36,7245 + 0,0026, ∆а* = 0,0026<0,005, а поэтому верными цифрами числа а* являются его цифры – 3, 6, 7, 2. Округление а* дает (а*)* = 36,72. Суммарная погрешность (а*)*: ∆((а*)*) = ∆(а*) + ∆(окр а*) = 0,0026 + 0,0045 = 0,0071>0,005

Поскольку ∆((а*)*)>0,005, то необходимо в (а*)* уменьшение цифр путем округления числа. Имеем ((а*)*)* = 36,7. В этом случае:

∆(((а*)*)*) = ∆(а*) + ∆(окр) = 0,0026 + 0,0245 = 0,0271<0,05.

Это означает, что верными цифрами приближенного числа а* = 36,7245 ± 0,0026 являются 3, 6, 7.

Пример

Округлить сомнительные цифры приближенного числа а* = 22,7314, оставив верные цифры. Определить абсолютную погрешность, если δ(а*) = 0,2%.

Решение

Заданная относительная погрешность числа в виде десятичной дроби имеет вид δ(а*) = 0,002. С учетом ∆(а*) = а*∙δ(а*) имеем истинную абсолютную погрешность ∆(а*) = 22,7314∙0,002 = 0,0454628 ≈ 0,0455

Так как эта погрешность меньше 0,05, то верных цифр числа а* будет три – 2, 2, 7. Округлим а* до десятых долей, имеем (а*)* = 22,7. Суммарная погрешность (а*)* равна ∆((а*)*) = ∆(а*) + ∆(окр) = 0,0455 + 0,0314 = 0,0769.

Поскольку эта погрешность больше 0,05, то уменьшается число цифр приближенного числа а* до двух, т.е. ((а*)*)* = 23, имеем:

∆(((а*)*)*) = ∆(а*) + ∆(окр) = 0,0455 + (23 – 22,7314) = 0,0455 + 0,2686 = 0,3141<0,5

Это означает, что в полученном округленном числе ((а*)*)* обе цифры, т.е. 2 и 3 являются верными.

Последние два примера показали, что округление результата расчета до верных знаков не всегда целесообразно.

Формула верных знаков приближенного числа

Абсолютная погрешность m-разрядного приближенного числа, т.е. ∆(а*), связана с числом его верных знаков n соотношением

∆(а*) ≤ 0,5∙10^m-n+1 , что следует из определения верной значащей цифры а*.

Записав а* как десятичную дробь, т.е. а* = α1∙10^m + α2∙10^m-1 +…+ αn∙10^m-n+1, имеем очевидное неравенство:

Δ(а*) = ∆(а*)/│а*│≤ (0,5∙10^m-n+1)/│десятичн. представ.│ ≤ 0,5∙10^m-n+1/α1∙10^m, позволяющее записать предельную (граничную) относительную погрешность в виде δ*(а*) = 0,5/α1∙10^n-1

Эта формула связывает между собой граничную относительную погрешность приближенного числа а*, первая цифра которого α1 известна, с числом верных знаков этого числа.

Пример

Предельная относительная погрешность приближенного числа а* = 4,176 со всеми верными цифрами равна:

δ*(а*) = 0,5/4∙10^4-1 = 0,000125 (Здесь α1 = 4, n = 4)

Пример

Сколько верных десятичных знаков надо взять при вычислении √19, чтобы δ*(а*) не превышала 0,1. n = ?

Имеем 0,001 ≤ 0,5/4∙10^n-1 ≤ 1,25/10ⁿ, или 10n ≤ 1250 = 1,25∙10³; n ≤ lg1,25 + 3,.. –e δ*(a*) ≤ 0,5/4∙10² = 0,125%. Поскольку δ*(a*) должно быть 0,1%, то следовательно n ≥ 3 + lg1,25, т.е. можно принять n = 4.

Примечание

Относительная точность приближенного числа определяется только количеством его значащих цифр, а положение запятой при этом никакого значения не имеет. 743,8, 0,007438, 7438 имеют одинаковую относительную погрешность, т.к. для них δ(а*) = 0,000067.

Пример

Какое из приближенных чисел а₁* = 0,000001, а₂* = 98,1 задано более точно?

Решение

δ(а₁*) = 0,0000005/0,000001 = 0,5. δ(а₂*) = 0,05/98,1 = 0,00051, т.е. приближенное число а₂* можно определить в тысячу раз точнее, чем а₁*

Вычисление с учетом погрешностей

При выполнении операций над приближенными числами неизбежно происходит накопление погрешностей. Ниже покажем, как, зная погрешности операндов, можно определить абсолютные и относительные погрешности результата арифметических действий над ними.

А) Погрешности суммы и разности

1. При сложении двух приближенных чисел а_i* = а_i ± ∆(а_i), i € {1,2} получаем результат а₁* + а₂* = а1 + а2 ± ∆(а₁*) ± ∆(а₂*)

Действительно:

а₁* - ∆(а₁*) < a₁ < a₁* + ∆(a₁*)

+

а₂* - ∆(а₂*) < a₂ < a₂* + ∆(a₂*)

___________________________

(a₁* + a₂*) – (∆(a₁*) + ∆(a₂*)) < a₁ + a₂ < (a₁* + a₂*) + (∆(a₁*) + ∆(a₂*))

Итак, в иной записи, имеем:

а1* + а2* = а1 + а2 + (±∆(а₁*) ± ∆(а₂*))

Отсюда получаем:

∆(а₁* + а₂*) = (±∆(а₁*) ± ∆(а₂*))

Поскольку истинные знаки погрешностей ∆(а₁*) и ∆(а₂*) в общем случае неизвестны, то для достоверности результата следует брать наихудший случай – т.е. когда погрешности складываются:

∆*(а₁* + а₂*) = ∆*(a₁*) + ∆*(a₂*)

Пользуясь методом полной математической индукции, легко доказать результат для k операндов:

∆* (∑ i=1 по k a_i*) = ∑ i=1 по k ∆*(a_i*)

Итак, приходим к следующему утверждению: «Граничная абсолютная погрешность суммы операндов равна сумме граничных абсолютных погрешностей слагаемых».

Пример

Согласно пятизначным таблицам логарифмов, lg1,1 = 0,04139; lg1,14 = 0,05690. Имеем: lg1,1 + lg1,14 = 0,09829 = lg1,254, а непосредственно из таблицы lg1,254 = 0,09830

Расхождение результатов становится понятным, если обратиться к семизначным таблицам, согласно которым lg1,1 = 0,0413927; lg1,14 = 0,0569049. В этом случае: lg1,1 + lg1,14 = 0,0982976 ≈ 0,09830

Сформулированное выше утверждение дает возможность оценить точность получаемой суммы и предвидеть, с какой точностью надо взять слагаемые, для того, чтобы гарантировать необходимую точность результата.

Пример

Найти сумму приближенных чисел 5,8; 287,649; 0,308064.

Решение

Из трех вариантов сложения этих чисел правильным являтся третий.

5,8 5,8 5,8

287,649 287,6 287,65

0,308064 0,3 0,31

_________ _____ ______

293, 757064 293,7 293,76 ≈ 293,8

Действительно, в числе 5,8??? Отброшенные цифры нам неизвестны, так что не имеет никакого смысла к неизвестным цифрам прибавлять известные и получать результат с точностью до миллионных, которая ничем не гарантированна.

Второй вариант также неверен, т.к. совершенно не использует большую точность двух других слагаемых.

Пример

Вычислить сумму √2 + √3 + √10 с тремя десятичными знаками.

Решение

Поскольку сумму приближенных чисел надо получить с тремя десятичными разрядами, то каждое из слагаемых следует вычислить с одним запасным знаком √2 ≈ 1,4142; √3 ≈ 1,7321; √10 ≈ 3,1623. Тогда имеем 1,4142 + 1,7321 + 3,1623 = 6,3086 ≈ 6,309.

Итак, при сложении чисел различной абсолютной точности следует поступить следующим образом:

- выделить число (или числа) наименьшей абсолютной точности (т.е. число, имеющее наибольшую абсолютную погрешность);

- наиболее точные числа округлить так, чтобы сохранить в них на один знак больше, чем в выделенном числе (т.е. оставить один запасной знак);

- произвести сложение, учитывая все сохраненные знаки;

- полученный результат округлить на один знак.

Следует, однако, отметить, что формула ∆* (∑ i=1 по k a_i*) = ∑ i=1 по k ∆*(a_i*) при большом количестве слагаемых (практически больше 10) дает завышенную оценку абсолютной погрешности суммы, т.к. обычно происходит частичная компенсация погрешностей разных знаков. Если все слагаемые округлены до m-го десятичного разряда, т.е. их погрешности оцениваются величиной 0,5∙10^-m, то статистическая оценка абсолютной погрешности суммы дается правилом Чеботарева:

∆(∑ i=1 по k a_i*) = √(3n) ∙ 0,5∙10^-m , где n – число слагаемых. Это правило применяют для n > 10.

2) При вычитании приближенных чисел их погрешности также вычитаются, но алгебраически, т.е. когда обе погрешности одного знака, они вычитаются, а когда знаки различны, то складываются. Поэтому как и в случае сложения, граничная абсолютная погрешность разности двух приближенных чисел равняется сумме их граничных абсолютных погрешностей: ∆*(а₁* - а₂*) = ∆*(а₁*) + ∆*(а₂*).

Для того чтобы отнять одно приближенное число от другого, прежде надо одинаково их округлить.

Пример

а₁* = 27,613 отнимаем от а₂* = 546,3 так: 546,3 – 27,6 = 518,7

При этом нет никаких оснований писать 546,3 – 27,613 = 518,687, т.к. в числе 546,3??? Цифры сотых и тысячных нам неизвестны и заменять их нулями нет никаких оснований.

Пример

Разность чисел а₁* = 5,847 и а₂* = 2,342, имеющих все верные цифры, равна:

_ 5,874 ± 0,0005

2,342 ± 0,0005

3,532 ± 0,001

Здесь последняя десятичная цифра разности является сомнительной.

Очевидно, что в результате вычитания двух близких чисел может произойти большая потеря точности. Так, например, 985,437 – 985,421 = 0,016 есть разность двух чисел, из которых каждое имеет шесть значащих цифр, сохранившая только две значащие цифры, причем полученный результат может иметь погрешность до одной единицы последнего разряда (т.е. 0,0005 + 0,0005 = 0,001).

Избежать таких погрешностей можно либо взяв при вычитании двух близких величин их приближения с достаточно высокой точностью, либо исключив разность близких величин, либо вычислив эту разность непосредственно с максимально возможной точностью.

Пример

Найти число а* = √4,300 - √4,287 с двумя значащими цифрами.

Решение

Если √4,300 ≈ 2,0736, √4,287 ≈ 2,0705, то будем иметь а* = 2,0736 – 2,0705 = 0,0031

Этот же результат проще получить при помощи преобразования вычислительной схемы: √4,300 - √4,287 = (4,300 – 4,287)/( √4,300 + √4,287) = 0,013/(2,07 + 2,07) = 0,0031

В данном случае корни надо было найти только с двумя значащими цифрами, что имеет принципиальное значение, т.к. встречается немало задач, в которых каждый дополнительный знак точности требует выполнения значительного объема работы.

Пример

Вычислить площадь концентрического кольца S = π[(r + x)² – r²].

Если х мало, то непосредственное вычитание дает большую потерю точности. Поэтому целесообразно вести расчет по формуле: S = π(2xr + x²) = π(2r + x)x

В тех случаях, когда нет возможности ни преобразовать данную расчетную формулу, ни обеспечить вычисление промежуточных данных с необходимой степенью точности, разность двух близких величин может полостью обесценить результат всех предыдущих вычислений.

3) Относительная погрешность суммы положительных (отрицательных) чисел имеет вид:

δ(∑ i=1 по k a_i*) = (∑ i=1 по k ∆(a_i*))/(∑ i=1 по k a_i*)

Учитывая, что а_i*∙δ(a_i) = ∆(a_i*) и принимает a_i > 0, получаем оценку:

δ_min(a_i*) = δ_min(a_i*)(∑ i=1 по k a_i*)/(∑ i=1 по k a_i*) < δ(∑ i=1 по k a_i*)< δ_max(a_i*)(∑ i=1 по k a_i*)/(∑ i=1 по k a_i*) = δ_max(a_i*)

т.е. относительная погрешность суммы слагаемых одного знака заключена между наименьшей и наибольшей относительными погрешностями слагаемых.

Пример

Оценить относительную погрешность суммы чисел, имеющих верные цифры: 0,1732; 17,45; 0,000333; 204,4; 7,25; 144,2; 0,0112; 0,634; 0,0771. Сравнить ее с относительными погрешностями слагаемых.

0,1 7

17,4 5

0,0 0

204,4

7,2 5

144,2

0,0 1

0,6 3

0,0 8

374,1 9

Округляя результат суммирования заданных приближенных чисел, получаем окончательную ∑ i=1 по 9 a_i* = 374,2

Оценка полученного результата:

- предельная погрешность исходных данных равна 0,00005 + 0,005 + 0,0000005 + 0,05 + 0,005 + 0,05 + 0,00005 + 0,0005 + 0,00005 = 0,1106505 < 0,111

- погрешность округления слагаемых равна 0,0032 + 0,000333 + 0,0012 + 0,004 – 0,0029 = 0,005833 < 0,006

- погрешность округления равна – 0,01

Следовательно, ∆*(∑ i=1 по 9 a_i*) = 0,1106505 + 0,005833 – 0,01 ≈ 0,107

Искомая сумма есть 374,2 ± 0,107

Относительная погрешность суммы

δ(∑ i=1 по 9 a_i*) = 0,107/374,2 = 0,00027 = 0,027%

Граничные относительные погрешности слагаемых составляют соответственно:

0,5/ 1732 ≈ 0,029% ; 0,5/ 1745 ≈ 0,0285% ; 0,5/ 333 ≈ 0,15% ; 0,5/ 2044 ≈ 0,0245% ; 0,5/ 725 ≈ 0,07% ; 0,5/ 1442 ≈ 0,0345 ; 0,5/ 112 ≈ 0,445% ; 0,5/ 634 ≈ 0/08% ; 0,5/ 771 ≈ 0,065%.

δ_max* = 0,445% ; δ_min* = 0,0245%

Итак, δ_min* < 0,027% < δ_max*

4) Относительная погрешность разности двух величин одного знака имеет вид:

δ*(а₁* - а₂*) = (∆(а₁*) + ∆(а₂*)) / │а₁* - а₂*│

Очевидно, что если а₁* и а₂* близки друг к другу, то даже при очень малых абсолютных погрешностях ∆(а₁*) и ∆(а₂*) (знаки которых могут быть любыми) величина относительной погрешности может быть весьма значительной.

Пример

Пусть √4,300 ≈ 2,0736 ± 0,00005 = а₁*, √4,287 ≈ 2,0705 ± 0,00005 = а₂*

Относительная граничная погрешность при вычислении каждого из корней равна δ*(а₁*) = δ*(а₂*) = 0,00005/2,07 = 0,000024, а относительная граничная погрешность разности √4,300 - √4,287 ≈ 0,00031 ± 0,00005 равна δ*(а₁* - а₂*) = 0,00005/0,0031 ≈ 0,016, т.е. δ*(а₁* - а₂*) более чем в 600 раз грубее исходных данных.

Очевидно, что при вычитании близких друг другу чисел (особенно если невозможно изменение вычислительной схемы) необходимо их брать с достаточным числом запасных верных знаков.

Так, если известно, что первые m значащих цифр могут пропасть, а результат надо получить с n верными знаками, то исходные данные необходимо брать с m + n верными значащими цифрами.

Б) Погрешность произведения и частного

• Формулы для непосредственного вычисления абсолютных погрешностей умножения и деления приближенных чисел громоздки, и поэтому в этих случаях сначала вычисляют относительную погрешность, а затем с учетом δ(а*) = ∆(u*)/ │u*│ находят ∆(u*) (здесь u* = а₁*∙а₂*∙…∙а_n*) или u* = a₁*/a₂* = a₁*∙(1/a₂*)

Имея в виду, что a_i = a_i* ± ∆(a_i*) = a_i*(1 ± ∆(a_i*)/a_i*) = a_i*(1 ± δ(a_i*)), запишем операнды в виде

a₁*[1 – δ(a₁*)] < a₁ < a₁*[1 + δ(a₁*)]

a₂*[1 – δ(a₂*)] < a₂ < a₂*[1 + δ(a₂*)]

Почленно перемножая, имеем:

a₁*∙a₂*[1 – δ(a₁*)]∙[1 – δ(a₂*)] < a₁∙a₂ < a₁*∙a₂*[1 + δ(a₁*)]∙[1 + δ(a₂*)]

Произведение а₁∙а₂ с учетом [1 ±δ(a₁*)]∙[1 ±δ(a₂*)] = 1 ± [δ(a₁*) + δ(a₂*)] + [δ(a₁*)∙[δ(a₂*)] ≈ 1 ± [δ(a₁*) + δ(a₂*)]

Перепишем так:

a₁*∙a₂*[1 – δ(a₁*) – δ(a₂*)] < a₁a₂ < a₁*∙a₂*[1 + δ(a₁*) + δ(a₂*)]

это означает, что

a1∙a2 = a₁*∙a₂*[1 ± δ(a₁*) ± δ(a₂*)] = a₁*∙a₂*[1 ± ∆(a₁*a₂*)/ │ a₁*∙a₂*│] = a₁*∙a₂*[1 ± δ (a₁*a₂*)

или δ*(а₁*а₂*) = δ*(а₁*) + δ*(а₂*)

Очевидно, что если ∏ i=1 по k a_i* = а₁*∙а₂*∙…∙а_k*, то δ*(∏ i=1 по k a_i*) = ∑ i=1 по k δ*(a_i*) – т.е. при умножении приближенных чисел складываются их относительные, а не абсолютны погрешности.

Пример

Найти произведение чисел а₁* = 1,45 ± 0,01; а₂* = 2,28 ± 0,02; а₃* = 1,12 ± 0,01 и оценить его относительную и абсолютную погрешность.

Решение

δ*(1,45∙2,28∙1,12) = δ*(3,70) = 0,01/1,45 + 0,02/2,28 + 0,01/1,12 ≈ 0,025

Следовательно, произведение вычислено с погрешностью, не превышающей 0,025. Поэтому абсолютная погрешность ∆(3,71*) = 0,025∙3,71 < 0,093

Пример

Найти произведение чисел а₁* = 42,78 и а₂* = 0,0764, все цифры которых верные.

Решение

Так как а₁* и а₂* - приближенные числа, то в действительности они могут произвольно лежащими в интервалах:

42,775 ≤ а₁* ≤ 42,785,

0,07635 ≤а₂*≤ 0,07645

Очевидно, что произведение этих чисел заключено в интервале 42,775∙0,07635 – 42,785∙0,07645. Округляя до трех верных значащих цифр верхнюю и нижнюю границы произведения а₁*∙а₂*, получаем 3,268392 ≈ 3,27. Таким образом, если найдем произведение 42,78∙0,0764, то в этом результате 3,268392 ≈ 3,27 можно гарантировать надежность только первых трех цифр – ровно столько имеет значащих цифр наименьшее (в относительном смысле) число а₂* = 0,0764.

Замечание

В отдельных неблагоприятных случаях даже последняя из гарантированных цифр может быть сомнительной.

Пример

Произведение приближенных чисел а₁* = 0,108 ± 0,0005 и а₂* = 91,6 ± 0,05 не может иметь значащих цифр больше, чем три, поскольку каждый множитель содержит три верных знака. Поэтому a₁*∙a₂* = 1,108∙91,6 = 9,8928 ≈ 9,89

Действительно, нижней и верхней границами будут произведения 0,1078∙91,55 = 9,841625 ≈ 9,84 ; 0,1085∙91,65 = 9,944025 ≈ 9,94. Здесь последняя цифра произведения a₁*∙a₂* сомнительна и может иметь погрешность, составляющую пять единиц последнего разряда. Отсюда следует рекомендация: «для повышения точности произведения приближенных чисел, которые начинаются с единицы, надо стараться вычислять одну лишнюю значащую цифру».

Примечание

1. Если один из сомножителей произведения, например а₁, есть точное число, то δ(а₁∙а₂*) = δ(а₂*), т.к. δ(а₁) = 0. Из этого, в частности, следует, что относительная погрешность приближенного числа δ(а*) не зависит от положения запятой.

2. Абсолютная погрешность в случае, когда а1 – точное число, имеем ∆(а₁∙а₂*) = а₁∙а₂* δ(а₁∙а₂*) = а₁∙а₂* δ(а₂*) = а₁∙а₂*(∆(а2*)/а2*) = а1∙∆(а2*)

3. Если с_j – точное число, то ∆(∑ j=1 по k с_j∙a_j*) = ∑ j=1 по k с_j∙∆(a_j*)

• Поскольку деление на число а* равнозначно умножению на число 1/a*, то и относительная частного равна сумме относительных погрешностей делимого и делителя.

Рассматривая наименее благоприятный случай, определим абсолютную погрешность обратной величины равенством

∆(1/a*) = │1/a* - 1/(a* - ∆(а*)│ = ∆(а*)/((а*)² (1 - ∆(а*)/а*)) = ∆(а*)/((а*)² (1 – δ(а*))

Пренебрегая в этом равенстве величиной δ(а*) (вследствие ее малости по сравнению с 1), получаем: ∆(1/a*) = ∆(а*)/(а*)²

Очевидно, что δ(1/а*) = ∆(1/а*)/(1/а*) = (∆(а*)/(а*)²)/(1/а*) = ∆(а*)/(а*) = δ(а*)

Итак, δ(а₁*/а₂*) = δ(а₁*) + δ(1/а₂*) = δ(а₁*) + δ(а₂*)

Пользуясь методом полной математической индукции, легко доказать, что если даны положительные числа а₁*∙а₂*∙…∙а_m-1*, a_m*,…a_k*, то относительная погрешность выражения:

(∏ от i=1 по m–1 a_i*)/(∏ от j=m по k a_j*) = u_i*

оценивается величиной

δ(u*) = ∑ от i=1 по m–1 a_i* + ∑ от j=m по k a_j*

Замечание

При большом числе k целесообразна статистическая оценка, учитывающая частичную компенсацию погрешностей разных знаков. Если все числа числителя и знаменателя имеют примерно одинаковую относительную погрешность δ, то относительная погрешность частного принимается равной

Δ(u*) = (√3k)δ

Пример

Вычислить выражение u* = (3,2∙356,7∙0,04811)/(7,1948∙34,56), считая, что все приближенные числа заданы верными цифрами.

Решение

Наибольшую относительную погрешность здесь имеет число 3,2 (оно содержит всего два верных знака, против четырех – пяти верных знаков в остальных приближенных числах): δ(3,2*) = 0,05/3,2 = 0,016 = 1,6% Поэтому можно сказать, что относительная погрешность δ(u*) составляет 1,6%, т.е. что результат U* содержит не более двух верных знаков. Так как количество исходных чисел невелико, то в расчетах сохраняем один запасной знак, округляя все числа до трех знаков U* = (3,2∙357∙0,0481)/(7,19∙34,6) = 0,221

Абсолютная погрешность U* равна ∆(u*) = u*δ(u*) = 0,221∙0,016 = 0,0036. Округляя результат до верных знаков, отбрасываем запасной знак и получаем U* = 0,22 с абсолютной погрешностью ∆(u*) < 0,005. Очевидно, что если делитель есть точное число а₂ (тогда δ(а₂) = 0, ∆(а) = 0), то относительная погрешность частного a₁*/a₂* будет равна относительной погрешности δ(а₁*) приближенного числа а₁*. Абсолютная погрешность частного a₁*/a₂* уменьшится в а₂ раз.

Действительно, ∆(а₁*∙1/a₂) = а₁*∙1/a₂∙δ(а₁*∙1/a₂) = (а₁*/a₂)∙δ(a₁*) = ∆(a₁*)/a₂.

Возведение в степень приближенно числа всегда можно рассматривать как n-кратное умножение этого числа самого на себя. Поэтому относительная погрешность степени равна относительной погрешности основания, умноженной на показатель степени n. Это означает, что при возведении в степень относительная погрешность увеличивается пропорционально показателю степени, т.е. при возведении в квадрат относительная погрешность удваивается, в куб – утраивается и т.д.

Пример

Для числа а* = 3,712 ± 0,0005 имеем (а*)² = 13,778944 ± 13,778944∙(2∙0,0005)/3,712, т.е. 13,7752 < (а*)² < 13,7826, или (а*)² = 13,78.

Аналогично (а*)³ = 51,147440(1 ± (3∙0,0005)/3,712), 51,12677 < (а*)³ < 51,16811, или (а*)³ = 51,15

Т.к. U* = √а* k-ой степени, то а* = (U*)^k. Отсюда получаем δ*(а*) = kδ*(u*) и δ*(u*) = 1/k δ*(а*). При извлечении корня из приближенного числа относительная погрешность результата уменьшается пропорционально показателю корня. Это означает, что число значащих цифр в результате не меньше числа значащих цифр подкоренного выражения.

Пример

Для числа а* = 1,248 ± 0,0005 имеем √1,248 = 1,117, причем все цифры результата верны, т.к. √(1,248 – 0,0005) = √1,2475 = 1,11691….; √(1,248 + 0,0005) = √1,2485 = 1,11736….

Итак, (а*)^1/2 = 1,117

Число верных знаков частного определяется его предельной относительной погрешностью: δ(а₁*/а₂*) = δ(а₁*) + δ(а₂*) = 0,5/10^n-1(1/α₁ + 1/β₁), где а₁* = α₁∙10^l1 + α2∙10^l1-1+…; a2* = β1∙10^l2 + β2∙10^l2-1+… Следовательно, если α₁ ≥ 2 и β₁ ≥ 2, то частное имеет n – 1 значащую цифру. Если же α1= 1 и β1 = 1, то частное может иметь n – 2 значащие цифры.

Пример

Вычислить частное U* = 39,356/2,21, если в делимом и делителе все цифры – верные.

Решение

Поскольку в делителе три верных значащих знака, а в делимом пять, то последнее округляем до четырех значащих цифр и производим деление. 39,35/2,21 = 17,81…, т.е. U* = 17,8. Подсчитаем предельную относительную погрешность частного U*. Поскольку число значащих цифр менее точного числа (делителя) равно 3 (т.е. n=3), α₁ = 3, β₁ = 2, то получаем: δ*(39,356/2,21) = 0,5/10^3-1(1/3 – 1/2) = 5/12∙10^-2 = 0,42%. Таким образом, частное содержит две верные значащие цифры (т.е. на одну значащую цифру меньше, чем у делителя).

Пример

Определить предельную относительную погрешность частного U* = 15,834/1,72 и число верных значащих цифр.

Решение

В этом примере n = 3, α₁ = 1, β₁ = 1. Имеем δ*(u*) = 0,5/10^3-1(1/1 + 1/1) = 1∙10^-2. Отсюда следует, что частное содержит только одну верную значащую цифру (т.е. на две верные значащие цифры меньше, чем у делителя).

Правила подсчета цифр

При вычислениях, когда не проводится строгий подсчет погрешностей, рекомендуется пользоваться правилами подсчета цифр. Эти правила указывают, как следует проводить округления всех результатов, чтобы, во-первых, обеспечить заданную точность окончательного результата и, во-вторых, не производить вычислений с лишними знаками (не оказывающими влияние на верные знаки результата).

Приведем правила подсчета цифр, данные В.М. Браунсом:

1. Результат сложения и вычитания приближенных чисел должен сохранять столько значащих цифр, сколько их в приближенном данном наименьшей точности.

2. Результат умножения и деления должен сохранять столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр.

3. При возведении приближенного числа в квадрат или куб в результате следует сохранить столько значащих цифр, сколько их в основании степени.

4. При извлечении квадратного и кубического корней из приближенного числа в результате следует сохранить столько значащих цифр, сколько их в подкоренном числе.

5. При вычислении промежуточных результатов следует сохранить на одну цифру больше, чем рекомендуют правила 1 – 4. В окончательном результате эта «запасная» цифра отбрасывается.

6. Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при других действиях), чем другие, то их предварительно следует округлить, сохраняя лишь одну «запасную» цифру.

7. При вычислении с помощью логарифмов одночленного выражения рекомендуется подсчитать число значащих цифр в приближенном данном, имеющем наименьшее число значащих цифр и воспользоваться таблицей логарифмов с числом десятичных знаков на единицу большим. В окончательном результате последняя значащая цифра отбрасывается.

8. Если данные можно брать с произвольной точностью, то для получения результата с m верными цифрами исходные данные следует брать с таким числом цифр, которые согласно предыдущим правилам обеспечивают m + 1 цифру в результате.

Замечание

Эти восемь правил даются в предположении, что компоненты действий содержат только верные цифры и число действий невелико.

Пример

Пользуясь правилами подсчета цифр, вычислить πb*(a* - b*/3), если b* = 11,8; π = 3,142; a* = 23,67.

Решение

Находим 3,142∙11,8²(23,67 – 11,8/3) = 3,142∙139,2(23,67 – 3,933) = 3,142∙139,2∙19,373 = 437,37∙19,737 = 8630 = 8,63∙10³

Пример

Вычислить (а*³√b*)/c², где а* = 7,45 ± 0,01, b* = 50,46 ± 0,02, с = 15,4 ± 0,03. Определить погрешность результата.

Решение

При вычислении промежуточных результатов будем сохранять одну «запасную» цифру (т.е. если по общему правилу следует оставлять n значащих цифр, то в промежуточных результатах сохраняют n+1 цифр). Имеем: а*³ = 413,5, √b* = 7,1035, с² = 237,2, U* = 413,5∙7,1035/237,2 = 12,4

В этом результате оставлены три значащие цифры, т.к. наименьшее число значащих цифр в сомножителях равно трем.

Погрешность результата:

δ*(U*) = 3δ*(a*) + 1/2δ*(b*) + 2δ*(c) = 3∙0,01/7,45 + 1/2∙0,02/50,46 + 2∙0,03/15,4 = 0,00405 + 0,000195 + 0,0038 = 0,0081

∆*(U*) = U*δ*(U*) = 12,4∙0,0081 ≈ 0,11

Итак, получили U* = 12,4 ± 0,11; δ*(U*) = 0,81%

Пример

Рассчитать m*(a* + b*)/(c* - d*), если m* = 0.56 ± 0,0005; a* = 2,754 ± 0,001; b* = 11,7 ± 0,04; c* = 70,536 ± 0,002; d* = 6,32 ± 0,008.

Определить погрешность результата.

Решение

Находим (а* + b*) = 2,754 + 11,7 = 14,454; ∆*(a* + b*) = ∆*(a*) + ∆*(b*) = 0,001 + 0,04 = 0,041; (c* - d*) = 10,536 + 6,32 = 4,216; ∆*(c* - d*) = ∆*(c*) + ∆*(d*) = 0,002 + 0,008 = 0,010

Следовательно, U* = 0,56∙14,454/4,216² = 0,56∙14,454/17,75 = 0,456 ≈ 0,46

δ*(U*) = δ*(m) + δ*(a* + b*) + 2δ*(c* - d*) = 0,005/0,56 + 0,041/14,454 + 2∙0,01/4,216 = 0,00894 + 0,0028 + 0,00474 = 0,01648

∆*(U*) = U*δ*(U*) = 0,46∙0,016 = 0,007

Итак, получили ответ: U* = 0,46 ± 0,0077; δ*(U*) = 0,0165

Погрешности вычисления значений функции

Пусть некоторая величина U является дифференцируемой функцией n аргументов: U = f(x₁, x₂,…x_n), причем, определяя каким-то способом значения величины x_i, мы допускаем погрешности ∆ x₁, ∆ x₂,…∆ x_n. Тогда значение U, вычисленное по неточным значениям аргументов, получится с погрешностью ∆U, т.е.:

∆U = U ± U* = f(x₁ ± ∆ x₁, x₂ ± ∆ x₂,…x_n ± ∆ x_n)

Ниже приводится оценка погрешности ∆U, если известны погрешности аргументов ∆ x₁, ∆ x₂,…∆ x_n.

При достаточно малых абсолютных значениях величин ∆ x₁, ∆ x₂,…∆ x_n можно приближенно заменить полное приращение полным дифференциалом:

∆U ≈ ∑ от i=1 по k ∂f/∂x_i∙∆x_i

Здесь значения частных производных и значения погрешностей аргументов могут быть как положительными, так и отрицательными. Заменяя их абсолютными величинами, получим неравенство:

│∆U│ ≤ ∑ от i=1 по k │∂f/∂x_i│∙│∆x_i│

Для граничных абсолютных погрешностей, очевидно, можно принять

│∆*(U*)│ = ∑ от i=1 по k │∂f/∂x_i│∙│∆*(x_i*)│

Замечание

Если задана функция одного аргумента f(x) = y, то в этом случае │∆*(y)│ =│f’(x)│∙│∆*(x*)│, а относительная погрешность имеет оценку δ*(y*) = │∆*(y*)│/│y*│ = │f’(x)│/│f(x)│∙│∆*(x*)│ = [│lnf(x)│]’∙│∆*(x*)│

В частности, для основных элементарных функций получаем следующие правила:

А) Степенная функция y = f(x) = xα (α принадлежащем D)

Абсолютная погрешность этой функции равна ∆*(y*) = αx^α-1∙∆*(x*), а относительная погрешность δ*(y*) = │α│∙δ*(x*)

Так, если f(x) = x2, то относительная погрешность квадрата вдвое больше относительной погрешности основания x; если же f(x) = √x, то относительная погрешность квадратного корня вдвое меньше относительной погрешности подкоренного числа х; для f(x) = 1/x относительная погрешность обратной величины 1/x равна относительной погрешности самого числа х. Эти результаты полностью совпадают с полученными ранее.

Б) Показательная функция y = a^x (a>0).

Абсолютная и относительная погрешности соответственно равны: ∆*(y*) = │а^хlnа│∙│∆*(x*)│; δ*(y*) = │lna│∙δ*(x*)

Здесь относительная погрешность функции пропорциональна абсолютной погрешности аргумента.

Очевидно, что для функции y = e^x имеем ∆*(y*) = е^х∙│∆*(x*)│; δ*(у*) = ∆*(x*).

В) Логарифмическая функция y = log_ax. Учитывая, что (log_ax*)’ = 1/x*log_ae = 1/xlna, запишем абсолютные и относительные погрешности для натурального и десятичного логарифмов:

∆*(lnx*) = 1/x*∆*(x*) = δ*(x*); ∆*(lgx*) = 1/x*∆*(x*) = δ*(x*)∙lge = 0,4343 δ*(x*)

δ*(lnx*) = δ*(x*)/│lnx*│; δ*(lgx*) = 0,4343 δ*(x*)│lgx*│

Г) Тригонометрические функции

Абсолютная погрешность синуса и косинуса не превосходят абсолютных погрешностей аргумента:

∆*(sinx*) = │cosx*│ ∆*(x*) ≤ ∆*(x*)

∆*(cosx*) = │sinx*│ ∆*(x*) ≤ ∆*(x*)

Абсолютная погрешность тангенса и котангенса всегда больше абсолютной погрешности аргумента:

∆*(tgx*) = │1 + tg²x*│ ∆*(x*) ≥ ∆*(x*)

∆*(ctgx*) = │1 + ctg²x*│ ∆*(x*) ≥ ∆*(x*)

Пример

Диаметр круга, измеренный с точностью до 1мм, оказался равным d* = 0,842 м. Вычислить площадь круга S*.

Решение

Имеем S* = π∙d²/4. Поскольку число π можно взять для расчета с любой точностью, то погрешность вычисления площади определяется погрешностью d*². Относительная погрешность квадрата диаметра d* равна δ*(d*²) = 2 δ*(d*²) = 2∙1мм/842мм = 0,0024%

Чтобы при определении числа π не увеличить относительную погрешность площади круга, т.е. δ*(S*) = δ(π/4) + 22 δ*(d*), надо взять число π по крайней мере с четырьмя верными знаками (еще лучше с пятью). Тогда получим δ* = 3,1416/4∙0,842² м² = 0,7854∙0,7090 м² = 0,5568 м².

Абсолютная погрешность результата составляет: ∆*(S*) = S*∙δ*(S*) = 0,557∙0,0024 = 0,0014 м2. Округляя результат до трех знаков, получаем S* = 0,557 ± 0,002.

Пример

Определить sinx* и его абсолютную погрешность, если угол х* = 25 градусов 20’ ± 1’.

Решение

Поскольку ∆*(sinx*) = cosx*∆*(x*), то учитывая, что π = 180∙60’ и 1’ = 3,14/10800 = 0,000291 рад, имеем: ∆*(sin25 градусов 20’) = (cos25 градусов 20’)∙0,000291 = 0,00029

Поэтому для вычисления sinx надо взять четырехзначные таблицы тригонометрических функций, что дает sinx* ≈ sin25 градусов 20’ = 0,4279.

Пусть теперь заданы функции f(x,y)

Пример

Вычислить погрешности функций двух аргументов f₁(x,y) = xy; f₂(x,y) = x +y; f₃(x,y) = x – y; f₄(x,y) = x/y

Решение

∆*(f1*) = │x*│∆*(y*) + │y*│∆*(x*), δ*(f1*) = │x*│/│x*∙y*│∆*(y*) + │y*│/│x*∙y*│∆*(x*) = ∆*(y*)/│y*│ + ∆*(x*)/│x*│ = δ*(x*) + δ*(y*), т.е. максимальная относительная погрешность произведения равняется сумме максимальных относительных погрешностей сомножителей. Этот результат ранее мы получали из других предпосылок. Аналогично, используя полный дифференциал, имеем:

Отметим, как и ранее, что если иразности (-) близки, то может оказаться, что

будет очень велика по сравнению с определяемой величиной (). Это обстоятельство следует учитывать при производстве вычислений.

Пример: Гипотенуза «с» и катет «а» прямоугольного треугольника АВС, определенная с максимальными (граничными) погрешностями ,, соответственно равны,. Определить угол А по формуле :.

Решение:

Так как

, то имеем:

Таким образом,

Пример: Определить граничную абсолютную погрешность при вычислении катета прямоугольного треугольника АВС по формуле:, если катетугол

Решение: так как , то имеем:

Для оценки граничной (максимальной) относительной погрешности функции разделим левую и правую часть выражения граничной абсолютной погрешности на модуль функции:

Учитывая, что , имеем:

Итак, максимальная относительная погрешность функции равняется максимальной абсолютной погрешности логарифма этой функции. Из полученной формулы : легко получить ранее выведенные правила приближенных вычислений суммы, разности, произведения и частного.

Так, y=, тогда имеем :

Аналогично, если , то

Пример: Определить относительную погрешность вычисления периода колебания маятника Т, если его длина , ускорение силы тяжестим/и.

Решение: , то изполучаем:

Итак,

Пример: Вычислить ), еслии

Решение: Имеем

Определение допустимой погрешности аргументов по допустимой погрешности функции.

Эта задача имеет однозначное решение только для функций одной переменной . Еслидифференцируема ито:

Для функций нескольких переменных задача решается только при наложении следующих ограничений. Например, если полный дифференциалможно рассматривать как сумму всех равных между собой слагаемых, то применяют принцип равного влияния:

.

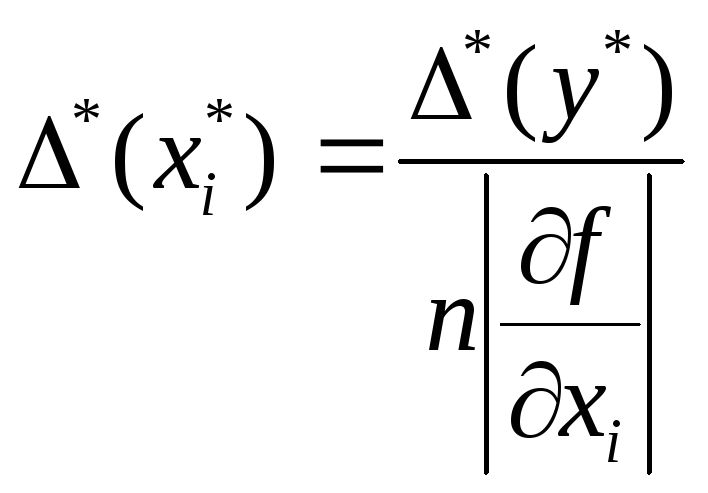Пример: С какой точностью нужно определить радиус r основания и высоту h цилиндрического стакана, чтобы его вместимость можно было определить с точностью до 1%.

Решение: В формуле , числоможно взять с любым числом верных знаков, так что его погрешность не скажется на результатах и поэтому логично считать, что. Поскольку можно обеспечить любую точность определенияr и h, то можно воспользоваться принципом равных влияний, откуда на долю иприходится по 0.5%. Это означает, что радиусr следует определить с относительной погрешностью 0.25% , а высоты h- с относительной погрешностью 0.5%.

Итак, беря с относительной погрешностью 0.01% (то есть, если возьмем=3.142, то), беремс тем, чтобы получить.

Пример: Найти допустимую абсолютную погрешность приближенных вычислений , для которых возможно найти значение функциис точностью до двух десятичных знаков после запятой.

Решение: Находим:

Поскольку по условию: , то согласно принципу равных влияний, то есть когда, имеем:

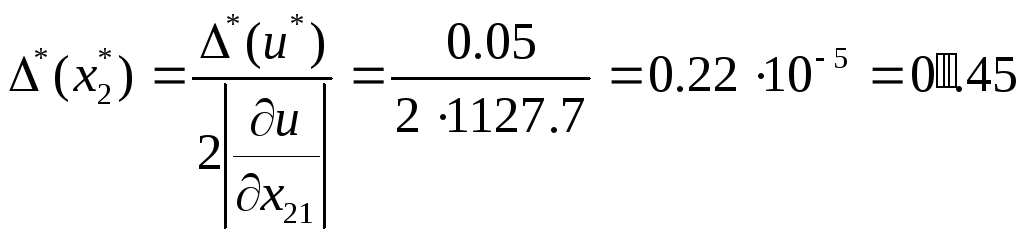
Оформление вычислений и ……243

Каждое вычисление надо проводить по тщательно разработанному алгоритму. Чаще всего алгоритм задают формулой, определяющей все действия, которые надо выполнить над исходными данными, для того, чтобы получить искомый результат.

Очень большое значение имеет также последовательность вычислений определенный действий, то есть программа вычислений.

Пример: Оформление программы (при ручном счете) вычисления с восемью значащими числами ( где х=10,n=5-точные числа) по формуле может быть следующая таблица:

				Контроль
0	1.5	5.06	0.39	при =3
1	1.59	6.391	0.3129
2	1.5849	6.3096818	0.3169732
3	1.5848932	6.3093756	0.316978692463
4	1.584893192403

Всегда следует помнить, что непроверенный результат вычислений ненадежен, и пока не осуществлен контроль, вычислений нельзя считать оконченными. Контроль надо начинать с проверки правильности исходных данных и расчетных формул.

Повторное вычисление по тем же формулам не гарантирует от повторения ошибок, поэтому более надежный контроль достигается вычислением по другим формулам или при помощи обратных действий (умножение проверяется делением, сложение - вычитанием и т.д.)

Приближенные методы решения конечных уравнений и систем.

Решение уравнений является одной из тех задач, которые наиболее часто встречается в практике инженера.

Однако, как массовая проблема, задача отыскания решения уравнения алгоритмически неразрешима в том плане, что не существует общего выражения для решения в виде формулы с конечным числом действий. Именно в этом случае приходится обращаться к методам, позволяющим отыскать приближенное решение заданного уравнения с любой наперед заданной точностью.

В читаемом курсе уравнением является выражение вида:

, где и- функциональные отображения элементов множества области отправленияв множество элементов области прибытия, то естьи

В том случае, если иесть множества чисел, то говорят о конечных уравнениях (алгебраических и трансцендентных). Еслииявляются точками многомерных пространств, то говорят о множестве о системе конечных уравнений. Если жеиявляются множествами функций, то в зависимости от видаибудем говорить о дифференциальных уравнениях, интегральных, интегро-дифференциальных.

Конечные уравнения.

Рассмотрим классификацию конечных уравнений согласно дереву:

Конечные уравнения

Трансцендентные уравнения

Алгебраические уравнения

Показательные

уравнения

Логарифмические

Алгебраические Алгебраические уравнения Тригонометрические

рациональные иррациональные уравнения

уравнения уравнения

Поскольку для конечных уравнений ,то. В частности, всякое уравнение с одним неизвестным можно представить в виде:, где-данные функции, определенные на некотором численном множествеM, называемом областью допустимых значений.

Уравнение с одним неизвестным можно записать в виде: .

Действительно, перенеся в левую часть уравнения, имеем уравнение:

. Если обозначить левую часть полученного уравнения через , то получим.

Решить уравнение - значит найти множество всех корней этого уравнения. Оно может быть конечным или бесконечным.

Пример: Уравнение имеет корни, так как:

то есть 4=4

то есть 1=1

Пример: Уравнение имеет решение. Придаваяn различные значения, получаем бесконечное множество корней.

Решить систему уравнений - значит найти множество всех ее решений, обращающих каждое уравнение системы в тождество.

Пример: Система:

имеет решение х=2, у=1 , так как при этих значениях неизвестных уравнения системы обращаются в тождества:

В зависимости от функции, входящих в уравнение уравнения разделяются на два больших класса - алгебраические и трансцендентные.

Функция называется алгебраической, если для получения значения функции по заданному значению переменной «х» нужно выполнить арифметические операции и возведение в степень с рациональным показателем

Иначе, алгебраической функцией называется функция , удовлетворяющая уравнению вида :, где-многочлен от х.

Алгебраическая функция называется рациональной относительно «х», если над «х» не производится никаких действий, кроме основных (умножение, деление, сложение и вычитание).

Пример:

Если в рациональную функцию переменная «ч» не входит в качестве делителя или не входит в выражение, являющейся делителем, то такая функция называется целой - рациональной (иначе – полином, многочлен)

Пример: ();

Так как действие вычитания может быть заменено действием сложения и умножения на постоянную величину с=-1:

,

то целой рациональной функцией (полиномом, многочленом) называется функция, которая может быть построена из независимого переменного посредством конечного числа сложений и умножений.

Алгебраическая рациональная функция вида:

, где и-многочлены :

; -постоянные, называемые коэффициентами () называется дробно- рациональной.

Иррациональное алгебраическое уравнение – алгебраическое уравнение, содержащее неизвестное под знаком радикала.

Пример:

Функция - иррациональная, а функцияне является иррациональной (т.к. «х» не стоит под знаком радикала).

Трансцендентное уравнение- уравнение, содержащие трансцендентные функции (то есть аналитические функции, не являющиеся алгебраическими) от неизвестного переменного. Очевидно, что трансцендентная функция не удовлетворяет уравнению вида:

Пример:

Для трансцендентных уравнений в настоящее время нет общих приемов их решения, кроме как приближенных.

Напоминание: Аналитическая функция- функция, которая может быть представлена степенным рядом.

Итак, если в запись уравнения входят только алгебраические функции, то уравнение называется алгебраическим.

Алгебраическое уравнение всегда может быть приведено к виду:

, где

Примечание: Если уравнение получено преобразованием уравнения, в которое входила дробная рациональная или иррациональная функция, то необходимо учитывать, что эти функции определены не на всей числовой оси.

Пример: Уравнение после освобождения от иррациональности примет вид:.

Однако первоначальное уравнение определено не на всей числовой оси, а для «х». принадлежащих отрезку [2;6]

Вычисление значений многочленов.

Пусть дано алгебраическое уравнение: . Вычислить значение многочленапри х=с можно непосредственной подстановкой «с» в полином, то есть находим:. Если при этом, то «с»-корень уравнения.

Вычисление значения многочлена тесно связано с вопросом о делимости полинома на линейный двучлен (полином первой степени).

Теорема Безу:

Остаток от деления многочлена на двучлен (х-с) равен значению этого многочлена при х=с

Доказательство:

Пусть , где-многочлен степени на единицу меньшей, чем.

В этом случае при х=с имеем:

что и требовалось доказать.

Следствие: Число «с» является корнем многочлена тогда и только тогда, если этот многочлен без остатка делится на двучлен (х-с).

Если многочлен делить на некоторый полином первой степени, то он делится, очевидно, и на многочлен, то есть на полином вида: (х-с). Следовательно, разыскание корней многочленаравносильно разысканию его линейных делителей.

Пример: Определить остаток от деления многочлена:

на двучлен (х-3).

Решение: По теореме Безу находим:

Действительно:

439

Итак, остаток r=439, а частное есть многочлен степени на единицу ниже, чем заданный полином.

На практике деление многочлена на линейный двучлен часто осуществляется по схеме Горнера.

Пусть записан в виде:

или:

Раскрыв скобки, имеем:

После приведения подобных членов, получаем:

В левой и правой частях последнего равенства находятся полиномы от переменной «х». Известно, что два многочлена считаются равными, если равны их коэффициенты при одинаковых степенях неизвестного «х», поэтому:

или

Из этих равенств видно, что каждый последующий коэффициент получается умножением предыдущегона «с» и прибавлением соответствующего коэффициента, так же находится и остаток.

Значение полинома на линейный двучлен удобно представить по следующей схеме:

Схема Горнера:

						…
с
						…

В первой строке этой схемы выписаны коэффициенты многочлена f(x) , а в третьей строке начинают с a₀ = b₀ , а затем каждый коэффициент b_i умножают на с и подписывают под следующий коэффициент a_i+1. Числа первой и второй строки соответствующего столбца складывают и результат b_i+1 записывают в третьей строке столбца. Таким образом в третьей строке записаны коэффициенты частного, полученного от деления многочлена f(c) на двучлен (x-c), и остаток, численно равный значению этого многочлена при x = c, т.е. b_n = f(c) = r.

Пример.

Пользуясь схемой Горнера, произвести деление полинома f(x) = x⁵ + 3x⁴ – 2x³ + x² – x + 1 на двучлен (x – 3).

Решение.

Составляем схему Горнера заданного многочлена.

	1	3	-2	1	-1	1
c = 3		3	18	48	147	438
	1	6	16	49	146	439

Отсюда: r = f(3) = 439, g(x) = x⁴ + 6x³ + 16x² + 49x + 146 следовательно

f(x) = (x – 3)( x⁴ + 6x³ + 16x² + 49x + 146) + 439

Пример.

Определить, является ли c = 1 корнем уравнения x³ + 2x² – 3 = 0

Решение.

Если c = 1 является корнем уравнения f(x) = x³ + 2x² – 3 = 0, то многочлен x³ + 2x² – 3 должен без остатка делиться на полином (x - 1).

Используем схему Горнера.

	a0 = 1	a1 = 2	a2 = 0	a3 = -3
c = 1		1*1	1*3	3*1
	b0 = 1	b2 =3	b2 =3	r = b3 =0

Итак, f(1) = 0 (остаток r = 0) и, значит, с = 1 является корнем заданного уравнения.

Примечание.

Целые рациональные функции (полиномы n-ой степени) f(x) = можно однозначно записать как произведениеf(x) = l₀(x - ₁)^k1(x - ₂)^k2…(x - _p )^kp , где =n, l_i – комплексные коэффициенты, _i - нули (корни) многочлена с кратностями k_1, k₂,…, k_p соответственно (основная теория алгебры).

В случае многочлена с действительными коэффициентами, основная теорема алгебры утверждает, что его можно разложить в произведение линейных и квадратных множителей с действительными коэффициентами:

= a₀(x – c₁)(x – c₂)…(x – c_l)(x² + p₁x + q₁)…(x² + p_kx + q_k), где 2k + l = n, a₀, c₁, c₂,…,c_l, p₁, p₂,…, p_l, q₁, q₂,…, q_l - действительные числа.

Если полином делится без остатка на (x - c_i)^k, но уже не делится на

(x - c_j)^k+1, то x_j – называется к – кратным корнем уравнения = 0 (корнем кратности к). В этом случаеx_j есть общий корень полинома и его производных вплоть до (к – 1)-ого порядка.

Для уравнения = 0 имеет место следующая зависимость между корнями уравненияc_j (с учетом кратности) и его коэффициентами a_j(i = 0, 1, 2,…, n);

c₁ + c₂ + … + c_n = = -a₁

c₁c₂ + c₁c₃ + … + c_n-1c_n = = a₂

c₁c₂ c₃ + c₁c₂c₄ + … + c_n-2c_n-1c_n =

c₁c₂ c₃…c_n = (-1)ⁿa_n

Это т.н. теорема Виета для квадратного и кубического уравнений.

x² + px +q = 0 x³ + rx² + jx + t = 0

дает

с₁ + с₂ = -p с₁ + с₂ + с₃ = -r

с₁с₂ = q с₁с₂ + с₁с₃ + с₂с₃ = j

с₁с₂с₃ = -t

Ни для какого алгебраического уравнения степени n >= 5 нельзя указать формулу, которая выражала бы его корни через его коэффициенты при помощи радикалов. Это теорема Абеля.

Если многочлен имеет комплексные корни, то их число – четное, т.к. комплексные корни обладают свойством парной сопряженности. Поэтому всякое алгебраическое уравнение нечетной степени с действительными коэффициентами имеет по крайней мере один действительный корень.

Подобно вычислительной схеме Горнера строят и схему деления многочлена на квадратный трехчлен.

Действительно:

= (x² + px + q)( ) +…+b_n-1x + b_n

Раскрывая скобки в правой части последнего равенства, произведя приведение подобных членов и сравнивая коэффициенты при одинаковых степенях x, получим:

a₀ = b₀

a₁ = b₁ + pb₀

a₂ = b₂ + pb₁ + qb₀

a₃ = b₃ + pb₂ + qb₁

…

a_n-2 = b_n-2 + pb_n-3 + qb_n-4

a_n-1 = b_n-1 + pb_n-2 + qb_n-3

a_n = b_n + pb_n-1 + qb_n-2

или

b₀ = a₀

b₁ = a₁ – pb₀

b₂ = a₂ – pb₁ – qb₀

b₃ = a₃ – pb₂ – qb₁

…

b_n-2 = a_n-2 – pb_n-3 – qb_n-4

b_n-1 = a_n-1 – pb_n-2 – qb_n-3

b_n = a_n – pb_n-1 – qb_n-2

Схема деления полинома на квадратный трехчлен.

Имеем следующую вычислительную схему деления полинома на квалратный трехчлен:

	a0	a1	a2	a3	…	an-2	an-1	an
p		-pa0	-pa1	-pa2	…	-pan-3	-pan-2
q			-qb0	-qb1	…	-qbn-4	-qbn-3	-qbn-2
	b0	b1	b2	b3	…	bn-2	bn-1	bn

Пример.

Разложить на множители полином f(x) = x⁵ – 2x⁴ – 4x³ – 33x² -30x -25, зная что один из корней есть с = -1/2 + i(3/4)^1/2

Решение.

Поскольку комплексные корни полинома попарно смежны, а заданный многочлен нечетной степени должен иметь хотя бы один действительный корень ( который обязательно служит делителем свободного члена a₅ = 25), то имеем

[(x+ 1/2) – i(3/4)^1/2][(x + 1/2 ) + i(3/4)^1/2] = x² + x + 1, (x - c) такое, что c = 1, или с = -1, с = 5, с = -5, с = 25, с = -25

Проверим по схеме Горнера какая с является корнем заданного полинома:

	1	-2	-7	-33	-30	-25
5		-5	35	-140	865	-4175
	1	-7	28	-177	835	-4200

Т.к. f(-5) не равно 0, то с = -5 не является корнем f(x).

Проверим теперь с = 5

	1	-2	-7	-33	-30	-25
5		5	15	40	35	25
	1	3	8	7	5	0

Итак f(5) = 0, т.е. с = 5 – корень f(x).

Заданный многочлен в соответствии с теоремой Безу можно записать в виде:

f(x) = (x - 5)(x⁴ + 3x³ + 8x² + 7x +5)

К тому же нам известен квадратный трехчлен x² + x + 1 и, поэтому, на него можно разделить полином 4 степени:

	q0 = 1	q1 = 3	q2 = 8	q3 = 7	q4 = 5
p = -1		-1	-2	-5	0
q = -1			-1	-2	-5
	b0 =1	b1 =2	b2 =5	b3 =0	b4 =0

Следовательно, заданный полином представим в виде произведения трех сомножителей с действительными коэффициентами, таким образом:

F(x)=(x-5)(x²+x+1)(x²+2x+5)

Итак, заданный полином имеет 5 корней

С₁=5, т.к. ч-5=0

С₂,₃=-1/2±i∙√3/2, т.к. х2+х+1=0

С₄,₅=-1±√(1-5) =-1±2i, т.к. х²+2х+5=0

Весьма существенным является определение приближенных значений действительных корней алгебраического уравнения (для получения линейных множителей), а также способ построения квадратичного множителя.

Для нахождения приближенного значения действительных корней уравнения ∑ i=1 по n a_ix^n-i=0 можно применять любые ниже изложенные методы (метод проб, хорд, касательных, итераций, комбинированные методы).

Квадратичный множитель можно выделить различными способами. Рассмотрим один из них – метод Хичкока.

В)) выделение квадратного трехчлена по методу Хичкока

Пусть задано алгебраическое уравнение f(x)=a_ix^n-i=0

Разделив полином … на трехчлен х²+px+q с неопределенными коэффициентами p и q, получим тождество:

…=(x²+px+q)g₁(x)+xf₁(p,q)+f₂(p,q), где g₁(x) – частное от деления f(x) на трехчлен …; f₁(p,q) и f₂(p,q) – многочлены от p и q.

Для того, чтобы указанный трехчлен был делителем полинома … необходимо и достаточно, чтобы полиномы f₁(p,q) и f₂(p,q) были равны 0, т.е. f₁(p,q)=0 и f₂(p,q)=0.

Решив систему f₁(p,q)=0

f₂(p,q)=0

найдем коэффициенты искомого квадратного трехчлена x+px+q.

Этот метод выделения квадратного трехчлена и называется методом Хичкока.

Разделив частное от деления g₁(x) на трех член x²+px+q, запишем тождество

G₁(x)=(x²+px+q)f₂(x)+xf₃(p,q)+f₄(p,q)

Подставив последнее выражение в тождество (*), получим

F(x)=(x²+px+q)2f₂(x)+ (x²+px+q)[xf₃(p,q)+f₄(p,q)]+xf₁(p,q)+f₂(p,q). (**)

После дифференцирования выражения по p и q имеем:

(f(x))’p=2x(x²+px+q)g₂(x)+(x²+px+q)2(g₂(x))’p+x₂f₃(p,q)+xf₄(p,q)+(x²+px+q)[x(f₃(p,q))’p+(f₄(p,q))’p+x(f₁(p,q))’p+(f₂(p,q))’p;

(f(x))’p=2(x²+px+q)g₂(x)+ (x²+px+q)2(g₂(x))’q+xf₃(p,q)+f₄(p,q)+ (x²+px+q)[x(f₃(p,q))’q+(f₄(p,q))’q]+x(f₁(p,q))’q+(f₂(p,q))’q.

Пусть L_i(i принадлежит {1,2} ) –корни квадратного трехчлена x²+px+q. В этом случае получаем:

α_i²+pα_i+q=0 (корень α_i обращает квадратный трехчлен в ноль). Следовательно,

α_i²=-pα_i-q.

С другой стороны, подставляя Li в (f(x))’p и (f(x))’q, имеем систему уравнений

α_i²f₃(p,q)+α_if₄(p,q)+α_i(f₁(p,q))’p+(f₂(p,q))’p=0

α_if₄(p,q)+f₄(p,q)+α_i(f₁(p,q))’q+(f₂(p,q))’q=0

Используя соотношение α_i² = -pα_i-q, перепишем последнюю систему в виде:

α_i[(f₁(p,q))’p+f₄(p,q)-pf₃(p,q)]+[(f₂(p,q))’p=(f₄(p,q))’

α_i[(f₁(p,q))’q+f₃(p,q)]+[(f₂(p,q))’q+f₄(p,q)]=0

Если α₁не=α₂, то из последней системы вытекает равенство нулю каждого из квадратных скобок, т.е.

(f₁(p,q))’p=pf₃(p,q)-f₄(p,q),

(f₂(p,q))’p=qf₃(p,q)

(f’(p,q))’q=-f₄(p,q)

(f₂(p,q))’q=-f₄(p,q)

Система (***) позволяет приближенно решить систему:

Действительно, если инепрерывно дифференцируемые функции и для них известны к-тые приближения неизвестныхи, то за более точные их значения можно принять;.

В этом случае система =0;с учетом линейных членов разложения функции в ряд Тейлора по степенями(членов более высоких порядков малы- отбрасываем) имеет вид:

или

Если определитель D этой системы не равен нулю, то она является определенной (то есть имеет единственное решение), а корни определяются формулами Крамера:

ФОРМУЛА

Замечание: Исходные значения иопределяются приближенно, обычно из графического решения.

Пример: Решить уравнение с точностью до 0.001 при помощи выделения квадратного трехчлена (квадратного множителя).

Решение: Отделим какие-либо два корня, определяя знаки функции при некоторых значениях аргумента «х»:

х	1	0	-1	-2	-3	-4
	+	-	-	-	-	+

Очевидно, что один корень лежит в интервале (0,1), другой- в интервале (-4,-3). Примем , а. В этом случае за начальное приближение квадратичного делителя заданного полинома можно взять в соответствии с теоремой Виета:, то есть имеем:

Расчеты оформим в виде двух вычислительных схем, первая из которых отражает двукратное деление полинома на квадратный трехчлен, а вторая для определения поправок и

к		1	4	4.8	16	-1
0	-p0 = -3 -q0 = 1,75 -p0 = -3 -q0 = 1,75	1 1	-3 -1/3 -2 = f3	-3 1,75 3,55 1,75 5.30 = f4	-10,65 1,75 7,1 = f1(p,q)	6,2125 5,2125 = f2

х	p0	f1(p0,q0)	f3(p0,q0)	f1(p0,q0)’p	f1(p0,q0)’q	D	∆D1	∆pk
	q0	f2(p0,q0)	f4(p0,q0)	f2(p0,q0)’p	f2(p0,q0)’q		∆D2	∆qk
0	3 -1,75	7,1 5,2125	-2 5,30	-11,3 3,5	2 -5,3	52,9	48,055 83,751	0,9 1,6

Итак, p₁ = p₀ ± ∆p₀ = 3 + 0,9 = 3,9

q₁ = q₀ ± ∆q₀ = -1,75 + 1,6 = -0,15

Повторив вычисления для p₁ и q₁, получим ∆p₁ = -0,11, ∆q₁ = -0,008; имея p₂ = p₁ ± ∆p₁ = 3,9 – 0,11 = 3,79 и q₂ = q₁ ± ∆q₁ = -0,15 – 0,008 = -0,27, после вычислений получим ∆p₂ = -0,0011, ∆q₂ = -0,0061. Для p₃ = p₂ ± ∆p₂ = 3,79 – 0,0011 = 3,7889 и q₃ = q₂ ± ∆q₂ = -0,23 – 0,0061 = -0,2361 вычисления дают ∆p₃ = -0,00005, ∆q₂ = 0,00003, а f₁(p₄,q₄) = 0,000076, f₂(p₄,q₄) = 0,000005, f₃(p₄,q₄) = 0,21115, f₄(p₄,q₄) = 4,236054, то можем записать:

Искомые корни найдем, решив квадратные уравнения:

1. 

, то есть

2.

то есть

Определение числа действительных корней алгебраического уравнения.

• Правило Декарта: Количество действительных положительных корней алгебраического уравнения с действительными коэффициентами (подсчитываемые столько раз, какова его кратность), либо равно числу перемен знаков в последовательности коэффициентов , либо на четное число меньше (равные нулю коэффициенты не учитываются).

Замечание: Сделав в уравнении =0 замену х=-у , можно определить число отрицательных корней уравнения.

Пример: Определить количество действительных корней уравнения

Решение: Согласно основной теореме алгебры это уравнение имеет пять корней (из них хотя бы один является действительным). Последовательность знаков коэффициентов этого уравнения такова: + - + + - +. Знак здесь меняется четыре раза и поэтому положительных действительных корней будет либо четыре, либо два раза, либо ни одного.

Принимая х=-у , получаем следующую последовательность знаков:- - - ₊₊₊. Из этого следует, что число отрицательных корней в нашем уравнении только одно.

Пример: Уравнение имеет либо 3, либо 1 положительных действительных корня, так как здесь: + - + + -, а число отрицательных корней также либо 3, либо 1. Это следует из следующей последовательности знаков коэффициентов заданного уравнения при х=-у : + - -+-

• Правило Штурма: Если действительные числа a и b (a < b) не являются корнями уравнения ==0 , то число действительных корней на отрезке [a , b] равно разности чисел перемен знаков в последовательностях функций и, где:

-остаток от деления нав точке, взятый с обратным знаком

- остаток от деления нав точке, взятый с обратным знаком

- остаток от деления нав точке с, взятый с обратным знаком.

- взятый с обратным знаком остаток , являющийся постоянной величиной от деления нав точке с.

Замечание: При помощи правила Штурма можно определить число отрицательных корней уравнения =0 ( то есть в интервале (-∞,0)) , а также число положительных корней уравнения в интервале (0, +∞)

Правило Штурма применяется также для отделения корней (то есть корень «с» уравнения считается отделенным на отрезке [a,b], если на этом отрезке уравнение не имеет других корней). Функции, входящие в систему Штурма, можно умножать и делить на произвольные положительные числа. Это значительно упрощает работу, когда производится деление с остатком.

Пример: Определить количество действительных корней уравнения , а также отделить эти корни, пользуясь правилом Штурма.

Решение: Составим кортеж функций Штурма.

Имеем:

Для определения умножимна 3 и разделим на:

_

x

-40x+9

То есть (остаток взяли с противоположным знаком).

Умножим на 8 и разделим 8на:

_40х-9

3х+27

40(27х-160)

27*40х-9*27

-6157

Поскольку этот остаток является постоянным числом со знаком минус, то получаем

Сведем в таблицу знаки компонент кортежа Штурма:

х					Число перемен знаков в кортеже
-∞	-	+	-	+	3
0	+	-	-	+	2
+∞	+	+	+	+	0

Из этой таблицы следует, что в интервале (-∞,+∞) заданное уравнение имеет три действительных корня, так как . Из них один корень отрицательный () , а два других - положительные ()

Отделим корни по правилу Штурма, сократив интервалы до длины, равной 1:

х					Число перемен знаков в кортеже
-∞	-	+	-	+	3
-3	-	+	-	+	3
-2	+	+	-	+	2
-1	+	-	+	+	2
0	+	-	-	+	2
1	-	-	+	+	1
2	+	+	+	+	0

Отсюда следует, что корни уравнения находятся в интервалах (-3,-2), (0,1), (1,2)

Теорема

Если все корни являются действительными числами, то для последовательности коэффициентов а₀, а₁,…а_k квадрат каждого не крайнего коэффициента больше произведения сходных с ним коэффициентов, т.е. а_k > a_k-1∙a_k+1

Нахождение области существования

корней алгебраического уравнения.

1. Правило Кольца. Корни алгебраического уравнения с действительными коэффициентами заключены в круговом кольце r<|x|<R, где r- внутренний радиус

, R- внешний радиус: ,

,

Замечание:R-верхняя, а r- нижняя границы положительных корней ; -R,-r- соответственно нижняя и верхняя граница отрицательных корней.

Пример: Определите границы корней уравнение

Решение: Здесь , А=20,,B=20, то есть:

Следовательно, действительные корни этого уравнения расположены в интервале (-5;5); при этом отрицательные корни лежат в интервале (-5;-0,013), а положительные- в интервале (0,013;5).

При решении уравнений удобно сначала установить границы корней, а затем применить правило Штурма. По правилу кольца эти границы определяются весьма приблизительно.

Приведем прием более точного определения границ действительных корней алгебраического уравнения