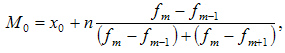25.Математическое ожидание непрерывной случайной величины:

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

называется величина , если число значений случайной величины конечно.

Если число значений случайной величины счетно, то .

При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле 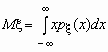. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то 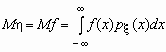Аналогичные формулы справедливы для функций дискретной случайной величины:

Основные свойства математического ожидания:

-математическое ожидание константы равно этой константе, Mc=c ;

-математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h );

-математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a;b], называют определенный интеграл: M(x)= x*f(x)dx . Если возможные значения принадлежат всей оси Ох, то: M(x)= xf(x)dx

26. Дисперсия и среднее квадратическое отклонение непрерывной случайной величины.

Дисперсией непрерывной случайной величины называется значение интеграла:

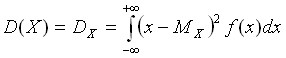
Среднее квадратичное отклонение непрерывной случайной величины вычисляется как корень квадратный из дисперсии:

Основные свойства математического ожидания и дисперсии непрерывных случайных величин остаются такими же, как и для дискретных случайных величин.

27.Моменты, коэффициенты асимметрии и эксцесса

Коэффицие́нт асимметри́и в теории вероятностей — величина, характеризующая асимметрию распределения данной случайной величины.

Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения ,или просто моментов (нецентральные моменты используются редко и здесь не будут рассматриваться). Величина третьего момента зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами либо наоборот. При нормаль- ном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов.

Показатели асимметрии: на основе момента третьего порядка можно построить показатель, характеризующий степень асимметричности распределения:

As называют коэффициентом асимметрии. Он может быть рассчитан как по сгруппированным, так и по несгруппированным данным.

Центральные моменты

Характеристика эксцесса распределения: с помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом.

Показатель эксцесса рассчитывается по формуле

Часто эксцесс интерпретируется как «крутизна» распределения, но это неточно и неполно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по оси абсцисс и по оси ординат, любое распределение можно искусствен но сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной ?) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено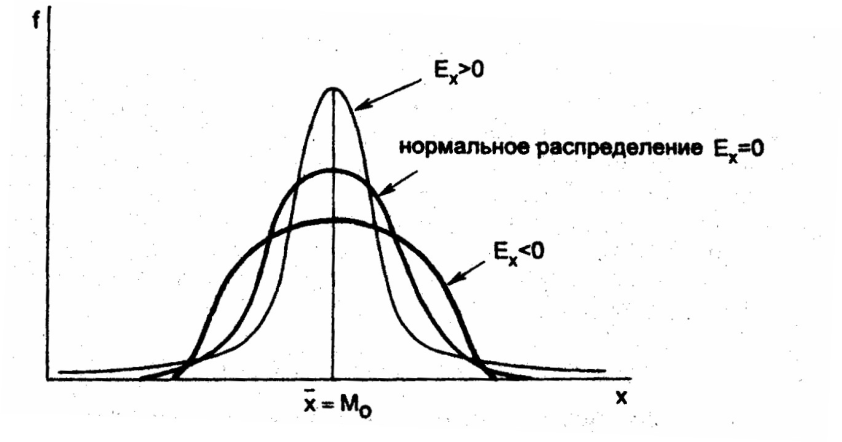

Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии дискретной случайной величины вычисляется по формуле:

As(X) = [(x1-M(X))3p1 + (x2-M(X))3p2 + ... + (xn-M(X))3pn]/σ3

Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее.

Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада». Коэффициент эксцесса дискретной случайной величины вычисляется по формуле:

Ex(X) = [(x1-M(X))4p1 + (x2-M(X))4p2 + ... + (xn-M(X))4pn]/σ4 - 3

28. Мода. Медиана: Медиана и мода - структурные (распределительные) средние величины.

Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.

Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда. Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина.

Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10) : 2= 8,5.

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле: