2.4. Вычисление коэффициентов регрессионной модели и метод наименьших квадратов.
Метод вычисления
коэффициентов
 в (2.10) называют методом наименьших
квадратов (сокращенно - МНК), если при
этом используется критерий наименьших
квадратов
в (2.10) называют методом наименьших
квадратов (сокращенно - МНК), если при
этом используется критерий наименьших
квадратов .
.
Для упрощения
записи будем использовать скалярную
переменную
 ,
что соответствует
,
что соответствует ,
но все формулы верны, если
,
но все формулы верны, если - это массив.
- это массив.
Запишем условия
минимума функции многих переменных
 :
:
 ,
,
и определим эти
частные производные, дифференцируя
 .
Получаем:
.
Получаем:
|

|
(2.12) |
Подставим сюда

 ,
,
 ,
,
изменим порядок
суммирования и обозначим через
 значение
значение -го
регрессора в
-го
регрессора в -ой
точке. Получаем систему
-ой
точке. Получаем систему уравнений с
неизвестными величинами
уравнений с
неизвестными величинами
 .
.
|
 , ,

|
(2.13) |
Система является
линейной и решается стандартными
методами. В результате получаем
оптимальные коэффициенты
 .
.
Вводя матрицу
коэффициентов системы (2.13),
 ,
,
и векторы
 ,
, ,
,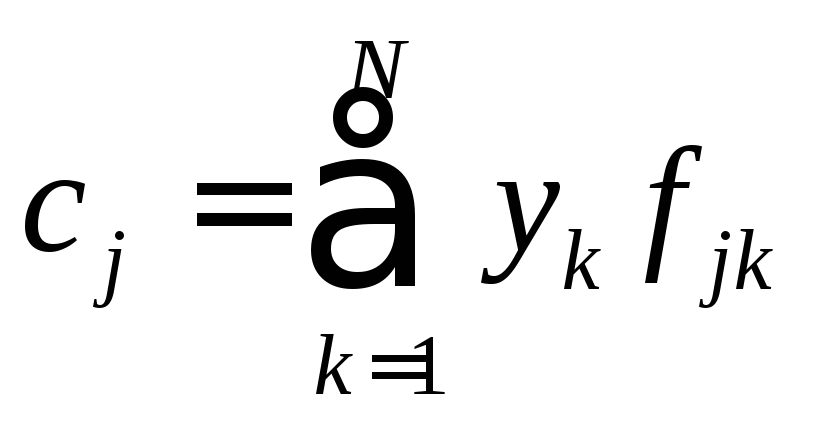 ,
запишем её в компактном виде:
,
запишем её в компактном виде:
|

|
(2.14) |
Часто вводят
регрессионную матрицу
 c элементами
c элементами .
.
 ;
;
транспонированная
матрица:
 .
.
Она полезна при
вычислениях
 ,
, ,
где
,
где ,
, .
.
Подчеркнем, что
полученная система линейна относительно
коэффициентов
 ,
а зависимость от входных параметров
,
а зависимость от входных параметров может быть
произвольной.
может быть
произвольной.
Пример регрессионной
модели.
Пусть имеем
 исходных точек,
исходных точек, входных параметра
входных параметра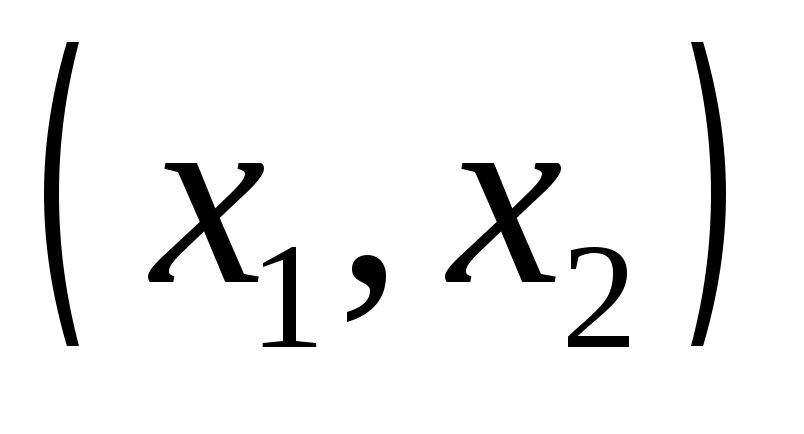 ,
, регрессора:
регрессора: ,
, ,
, ,
что соответствует регрессионной модели
,
что соответствует регрессионной модели .
Решив систему трех линейных уравнений,
получим аппроксимирующую функцию с
конкретными числовыми коэффициентами.
.
Решив систему трех линейных уравнений,
получим аппроксимирующую функцию с
конкретными числовыми коэффициентами.
Регрессорами могут
быть в частности полиномы или просто
степени
 ,
например:
,
например: ,
, ,
, ,
, ,
т.е.
,
т.е. ,
это аппроксимирующий полином.
,
это аппроксимирующий полином.
Достоинства
регрессионных моделей: простота,
наглядность, представление данных в
многомерном пространстве, наличие
стандартных статистических методов
для проверки их адекватности. Недостатки:
простота, произвольный выбор регрессоров,
малая область адекватности.
Для аппроксимации
в MathCAD
есть ряд стандартных функций: slope,
intersept,
loess,
regress,
linfit,
genfit.
При выполнении аппроксимации можно
провести предварительное сглаживание
данных и для этого использовать
стандартные функции MathCAD,
например supsmooth.



 ,
,
 ;
; .
.