9.3 Условие устойчивости для явных разностных схем.

Как и в случае ОДУ, решение УЧП должно быть устойчивым, точным, эффективным. Устойчивость важна для явных разностных схем, и при ее нарушении не будет сходимости численного решения к точному даже при очень мелких шагах дискретизации. Как и при решении ОДУ, неустойчивость связана с усилением шумовых составляющих решения. Условие устойчивости показывает, что изменения шагов дискретизации по разным независимым переменным должны быть согласованы для получения требуемой точности. Условие устойчивости существует для любой явной разностной схемы, и оно определяется уравнением и схемой. Например, для уравнения переноса с разностной схемой (9.8) условие устойчивости имеет вид

,

(9.10)

а уравнение теплопроводности (9.9) с разностной схемой, которой соответствует шаблон рис. 9.3, имеет условие устойчивости

,

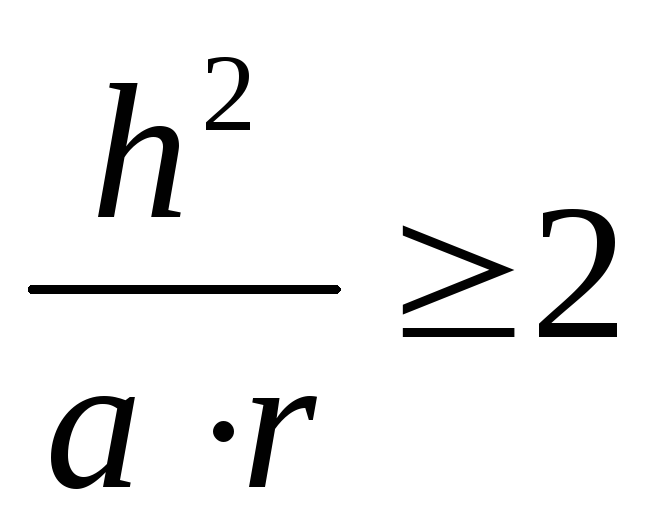(9.11)

Для вывода условия устойчивости можно применить спектральный метод. Он сравнивает амплитуды гармонических составляющих на соседних слоях рис. 9.1 Пусть для слоя с номером m рассматривается пространственная гармоника вида

,

(9.12)

где 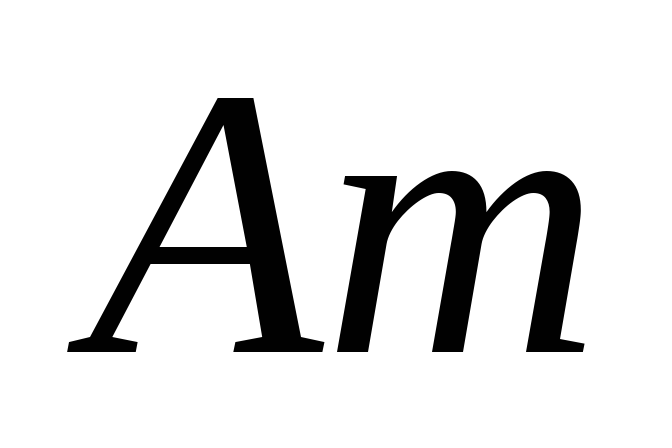- амплитуда гармоники, - волновое число, - шаг дискретизации по . На следующем временном слое эта гармоника изменит только свою комплексную амплитуду, т.е. будет иметь вид

.

(9.13)

Подставим (9.12), (9.13) в разностное уравнение (9.8) и получим отношение комплексных амплитуд

.

(9.14)

Устойчивость важна для убывающих решений (см. лекцию 7) и поэтому амплитуды любых гармоник, особенно шумовых, не должны возрастать, а иначе будет развиваться неустойчивость. Запишем это условие в виде

,

(9.15)

где

.

(9.16)

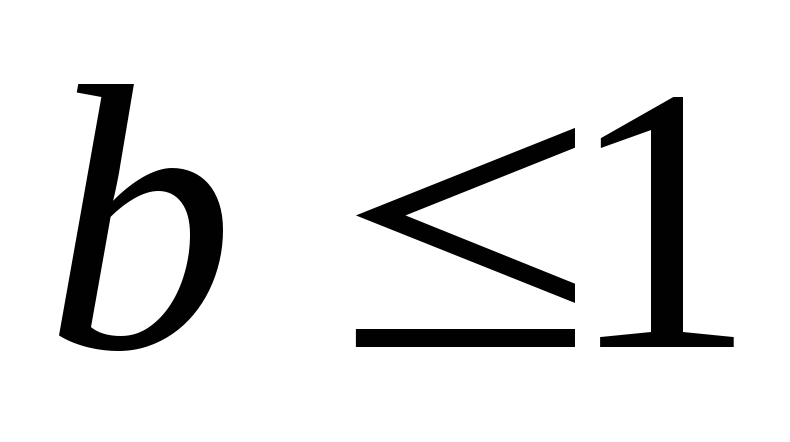Очевидно, что при для любых значений условие устойчивости не выполняется, и отсюда для уравнений переноса с разностной схемой (9.8) следует условие устойчивости , т.е. (9.10).