9.2. Метод конечных разностей (мкр).

Этот метод является самым простым численным методом решения уравнений в частных производных (УЧП). Название метода - МКР - связано с тем, что для вычисления производных в уравнении используется конечные разности вместо бесконечно малых разностей, которое входят в строгое определение производной через предел (lim) отношения. Рассмотрим основные этапы МКР на примере численного решения уравнения переноса (9.2).

1. Вводится сетка по всем переменным, т.е. выбираются шаги дискретизации по аналогии со случаем ОДУ, когда сетка определялась для одной переменной. Пусть ; - номера узлов для переменных и соответственно, и - шаги дискретизации по этим переменным, т.е.

,

(9.6)

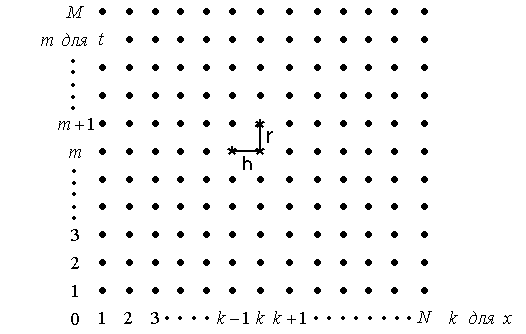
Количество шагов дискретизации и обычно очень велико. Очевидно, что в данном случае рассматриваемая область является прямоугольником с размерами и для каждой ее точки нужно найти значения , см. рис. 9.1.

Рис. 9.1. Сетка для решения (9.2) в прямоугольной области.

2. Непрерывная функция заменяется дискретной с целыми значениями аргументов , , т.е. она будет определена только в узлах сетки.

3. Производные в уравнении заменяются выражениями через конечные разности, т.е. используется численное дифференцирование. Например, используя простейшую формулу численного дифференцирования (4.2), представим производные в (9.2) следующим образом

, .

(9.7)

4. Полученные производные подставляются в уравнение, что дает одно уравнение или систему уравнений для определения неизвестных значений функции в узлах. Например, подставив (9.7) в (9.2), получаем

,

(9.8)

где значение .

Рассмотрим применение (9.8) для вычисления значений функции u на рис. 9.1. Пусть заданы начальные значения, т.е. при всех . Эти значения обычно называют нулевым временным слоем. Подставляя их в (9.8), находим все значения для следующего временного слоя с , кроме значения . Последнее можно определить, задав либо граничные условия, либо значения при . Аналогичным образом находим значения для следующего слоя с и т. д.

Формулу вида (9.8), связывающую значения исходной функции в соседних узлах, называют разностной схемой. Если изобразить точками узлы, которые применяются при вычислении производных в исходном уравнении, то получаем шаблон. Шаблон характеризует расположение узлов для разностной схемы. Например, разностной схеме (9.8) соответствует трехточечный шаблон, показанный на рис. 9.2 и 9.1

Рис. 9.2. Шаблон для уравнения переноса (9.2)

Выбор шаблона зависит от уравнения, применяемых формул численного дифференцирования, а также от вида дополнительных условий. Например, при решении уравнения теплопроводности для двух переменных

,

(9.9)

с начальными и граничными условиями обычно используются четырехточечный шаблон рис. 9.3.

Рис. 9.3. Шаблон для уравнения теплопроводности (9.9).

5. Решение разностных уравнений выполняется для всех узлов сетки и в результате получается искомая функция . Для простых разностных схем каждое разностное уравнение позволяет вычислить одно новое значение по заданным или вычисленным значениям в соседних узлах. Такие разностные схемы называются явными. Если же одно разностное уравнение содержит несколько неизвестных значений, то приходится составлять систему уравнений, а затем ее решать. Такие разностные схемы называются неявными по аналогии с неявными методами решения ОДУ, и они будут рассмотрены ниже.

6. Пусть значения в узлах сетки найдены. Теперь необходимо проверить правильность решения, т.к. выбор шагов дискретизации и был произвольным. Как и в лекциях 4, 7, для контроля точности следует использовать либо другие шаги, либо другой метод. Оба решения следует сравнить в совпадающих узлах двух сеток и за оценку погрешности принять максимальное различие полученных значений.

7. Если после получения решения для всех узлов сетки потребуется решение между узлами сетки, т.е. для дробных значений и , то можно применить интерполяцию или аппроксимацию функции многих переменных. Например, в случае двух независимых переменных и линейной интерполяции строится плоскость для трех соседних узлов, между которыми находится рассматриваемая точка.