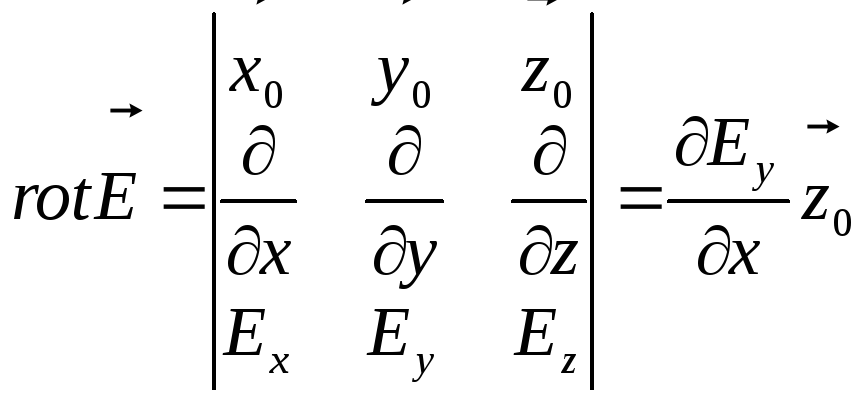-
Лекция 9. Метод конечных разностей для уравнений в частных производных
9.1 Уравнения в частных производных и дополнительные условия
В лекциях 6 - 8 рассматривались ОДУ, которые определяли функцию или вектор-функцию одной независимой переменной.
Уравнение в частных
производных - это дифференциальное
уравнение для функции многих переменных
и оно определяет связь частных производных
этой функции. В простейшем случае двух
независимых переменных, например,
,
,
уравнение в частных производных 1-го
порядка для функции
имеет вид
|
|
(9.1) |
Требуется найти
функцию
.
В общем случае в
входит производные более высоких
порядков, которые и определяют порядок
уравнения. При решении трехмерных задач
электродинамики, теплопроводности и
других искомых функций зависит от
четырех переменных – трех координат и
времени
.
Приведем ряд конкретных, часто
встречающихся уравнений.
Волновое уравнение
,
где
- оператор Лапласа, который в декартовых
координатах
,
,
имеет вид
,
- заданная функция, если
,
то имеем однородное волновое уравнение.
Приведем вывод волнового уравнения для плоской волны электромагнитного поля в вакууме, удовлетворяющего уравнениям Максвелла:
,
,
,
,
где
,
- напряженность электрического и
магнитного,
,
- плотность электрического тока и заряда,
возбуждающих поле,
,
- диэлектрическая и магнитная проницаемость
вакуума. В плоскости волны, распространяющейся
в направлении
,
существуют только две компоненты поля,
зависящее только от
,
(рис. 9.1).
,
|
|
|
Рис.9.1. Компоненты поля плоской волны. |
Учитывая, что в декартовых координатах
|
|
|
Получили из первых двух уравнений Максвелла
,
.
Дифференцируя
первое из этих уравнений по
,
а второе по
,
и исключая
,
придем к неоднородному волновому
уравнению для
:
,
где
- скорость света в вакууме
Уравнение Пуассона
.
Оно получается из уравнений Максвелла
для электростатического, не зависящего
от времени
поля (
),
когда
и можно ввести потенциал электрического
поля
,
т.к.
.
В декартовых
координатах, согласно определению
градиента для вектора
имеем
,
.
В результате из 4-го уравнения Максвелла получается уравнение Пуассона в декартовых координатах
.
В общем виде случае
произвольных координат получается
,
Оператор Лапласа
определяется при этом как
.
Уравнение Лапласа
.
Оно определяет потенциал электростатического
поля при отсутствии свободных зарядов,
,
когда поле возникает только из-за
разности потенциалов на отдельных
электродах, например на объкладках
конденсатора.
Уравнения
теплопроводности
,
определяет распределение температуры
в теле; постоянная «
»
определяется свойствами материала.
Уравнение
переноса.
Оно описывает распространение в
пространстве различных возмущений,
причем скорость распространения
характеризует величина
.
Нетрудно проверить, что при
любая функция вида
,
т.е. с аргументом
,
является решением (9.2) и поэтому для
определения конкретного решения должны
быть заданы дополнительные условия.
Обычно при решении уравнения в частных производных задают либо начальные условия, либо граничные, либо те и другие. Эти условия записываются в виде равенств со значениями или известными функциями в правой части. Например, начальное условие для (9.2) задается в виде
|
|
(9.3) |
,а граничное - в виде
|
|
(9.4) |
,
где
,
- конкретные заданные функции.
В случае уравнения (9.2) с начальным условием (9.3) получим решение
|
|
(9.5) |
.
Рисуя функцию с
различными сдвигами, получим распространение
возмущений вдоль оси
.