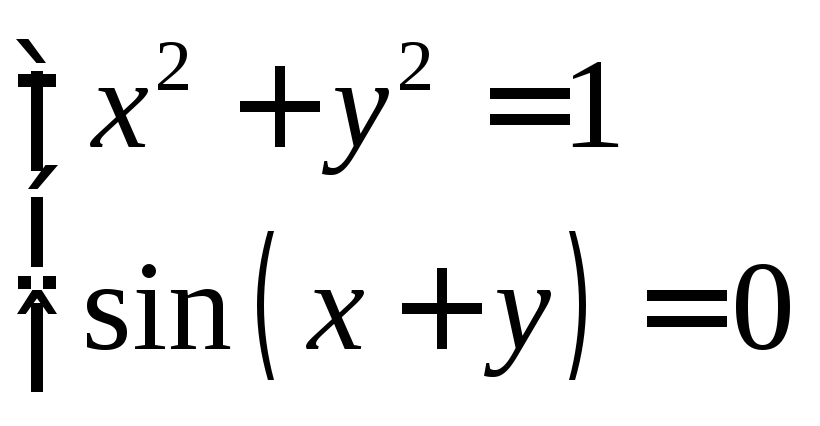5.5. Метод последовательных приближений (метод простых итераций).

Запишем исходное уравнение (5.1) в виде , это можно сделать разными способами, например вводя функциюсоотношением,

где произвольная не обращающаяся в нуль функция на интервале, где ищется корень. Зададим начальное значение корня, а затем будем вычислять последовательно,

При определенных условиях на функцию и удачном начальном значениипоследовательность,,… сходится, и получаем корень уравнения с погрешностью, еслис возрастанием.

Вместе с тем, сходимости может и не быть, в этом случае при вычислениях на ЭВМ можно поменять начальное приближение или функцию .

а) сходящийся процесс	б) расходящийся процесс
Рис. 5.5. Простые итерации при разных функциях .

Заметим, что простые итерации могут отображать реальные физические процессы. Например рис 5.5.а соответствует установлению определенной амплитуды колебаний в автогенераторе. Наоборот, рис. 5.5.б показывает существование в генераторе с определенной характеристикой колебаний с хаотическим изменением амплитуды. Такие колебания в настоящее время широко изучаются в физике, механике, радиоэлектронике, метеорологии и других областях науки.

5.6. Метод Ньютона при решении систем нелинейных уравнений.

Если в (5.1) рассматривать как массив функций длины, а- как массив неизвестных той же длины, то одно нелинейное уравнение становится системойнелинейных уравнений, например,

(5.5)

В примере , т.е. имеем систему двух нелинейных уравнений с неизвестными,. При записи систем нелинейных уравнений (СНУ) в общем виде используют как форму (5.1) с массивами, так и другие, например,

, или

(5.6)

Отметим, что в задачах моделирования современных электронных схем значения равны количеству узлов в схеме и обычно очень велики: от 100 до 1000000 и более, и для решения таких систем обычно применяют метод Ньютона.

Формулы для метода Ньютона в случае систем можно получить, заменив скалярные значения в (5.2 - 5.4) на массивы. При этом следует записать вместо одного уравнения (5.2) систему линейных уравнений вблизи точки

, ,

(5.7)

Производная в этом уравнении является матрицей Якоби , она составляется из всех частных производных всех функций и ее элемент

(5.8)

Матрица содержитстрок истолбцов, т.е. имеет порядок. Следовательно, одной итерации в методе Ньютона для СНУ соответствуют 2 формулы с векторами,,и матрицей:

,

(5.9)

Систему (5.9) можно записать по компонентам. Рассматривая ряд Тейлора для функции многих переменных из (5.6), пренебрегая членами со старшими производными.

,

Это же равенство получится, если умножить -ую строку матрицына вектор поправоки вычесть.

Метод Ньютона для многих переменных можно рассматривать как линейную интерполяцию гиперплоскостями в гиперпространстве вместо интерполяции прямыми на плоскости. Количество итераций в методе Ньютона для систем обычно не превышает 10..15.

В соответствии с (5.9) решение СНУ сводится к нескольким итерациями и на каждой итерации решается система линейных уравнений (СЛАУ) для нахождения вектора , т. е.

Если система нелинейных уравнений имеет несколько решений, то можно найти каждое из них, изменяя начальное значение .

Перечислим основные этапы метода Ньютона.

1. Выбор начального вектора и допустимой погрешности EPS.

2. Вычисление вектора для.

3. Вычисление матрицы Якоби для.

4. Решение СЛАУ (5.9) дает вектор поправок .

5. Получение нового вектора .

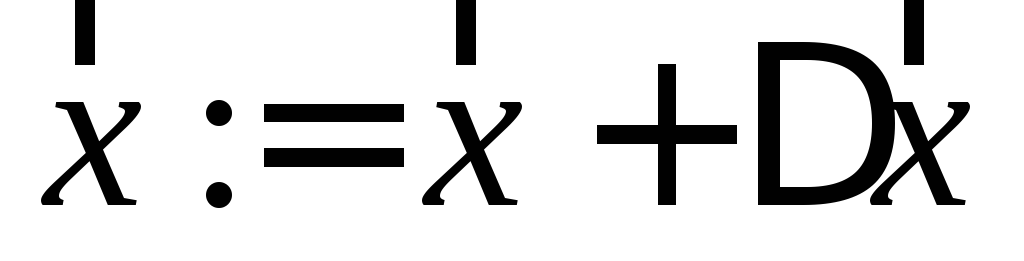6. Проверка условия окончания итераций . Если условие выполняется, то решение получено, иначе на пункт 2.

Норма в пункте 6 используется для оценки длины вектора, например, ее можно положить равной сумме модулей всех компонент вектора. Количество итераций обычно ограничивается для предотвращения зацикливания, например, при отсутствии решения системы. Значения EPS и погрешности аналогичны случаю одного уравнения.

Наиболее сложным этапом является вычисление матрицы Якоби. При этом используются формулы для частных производных в (5.8) или численное дифференцирование. Часто применяют упрощенный метод Ньютона, в котором пункт 3 переносится в пункт 1, т.е. матрица Якоби вычисляется только на первой итерации и не изменяется на последующих. На рис.5.2 это соответствует проведению прямых на итерациях, параллельных первой касательной. Упрощенный метод Ньютона используется при анализе электронных схем в программе PSpice.

В MathCAD для решения нелинейных систем есть функция Find, для которой составляется специальный блок уравнений Given. Функция Find реализует метод Ньютона. Возможно также применение функции Minerr , которая будет рассмотрена позже в разделе о минимизации функций.

В качестве примера рассмотрим решение системы (5.5) в MathCAD.

Given

Получили решение в виде вектора. Дополнительное условие может отсутствовать.  Значение , т.е. норме вектора в (5.6). Изменив начальные значения, получим другое решение с. В заключение посоветуем при решении сложных нелинейных систем сохранять мужество и оптимизм даже в случае применения хороших стандартных подпрограмм.