- 37 -

Лекция 5. Численные методы решения нелинейных уравнений и систем.

5.1. Решение одного нелинейного уравнения.

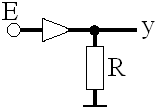
Рассмотрим математическую модель схемы с диодом и сопротивлением рис.1.3. Она является нелинейным уравнением, которое запишем в стандартном виде

,	(5.1)
где и значениенужно найти; (иконстанты диода)

В электродинамике широко применяются дисперсионные уравнения вида, связывающие значения частотыи волнового числа. Задавая значение частоты, получаем нелинейное уравнение вида (5.1), решив которое, определяем значение волнового числадля выбранной частоты.

В приведенных задачах, как и в других задачах проектирования, функции обычно очень сложны и для решения (5.1) применяют численные методы. Отметим, чтов (5.1) может быть задана алгоритмически и, например, требовать выполнения большого количества подпрограмм для вычисления каждого значения функции.

Постановка задачи:  дана функция на отрезке и нужно решить уравнение (5.1), т.е. найти его корень с погрешностью, не превышающей EPS.

Рис.5.1.

При этом задачу можно разбить на две:

1. Отделение корней, т.е. определение области, где лежит корень. Если например на отрезке выполняется условие, то функция меняет знак на этом отрезке и, следовательно, имеет корень. Если корней несколько, то либо найдем любой из этих корней, либо изменим отрезок, чтобы на нем был один корень.

Заметим, что определение корней с помощью графиков позволяет лишь грубо оценить значение корня, т.к. для задач проектирования характерны значения EPS = 10^-5 .. 10^-3.

2. Отыскание корней с заданной точностью.

Все численные методы нахождения корня являются итерационными. Итерация - это одно выполнение цикла и в латыни слово "itero" означает "многократно повторять". Итерационный метод соответствует циклическому выполнению группы вычислений, причем завершается цикл при получении правильного значения.

При решении (5.1) выполняются итерации и на каждой уточняется значение . При этом для каждого текущеговычисляются:

- значение ,

- значение поправки ,

- новое значение ,

- проверяются условия ,.

Если указанные условия выполняются, то решение получено, иначе  -  переход к первому пункту, т.е. вычислению значения.

Для проведения итераций должны быть решены следующие проблемы:

- как выбирать начальное значение для первой итерации,

- как вычислять поправку ,

- как уменьшить количество итераций при заданной погрешности EPS, что важно для сложных функций.

Рассмотрим, как решаются эти проблемы.

Вывод формул для поправки обычно основан на линейной или параболической интерполяции заданной функциивблизи текущей точки. Пересечение прямой или параболы с осьюдает новое значениедля следующей итерации. Чем сложнее метод определения, тем обычно меньше требуется итераций для нахождения корня с заданной погрешностью.

Выбор начального значения проводится на основании физических соображений или анализа поведения функции, можно также выбрать произвольное начальное значение ("с потолка"), если нет дополнительной информации.