- 61 -

Лекция 8. Численные методы решения систем оду.

8.1. Применение методов решения оду для систем оду.

В лекции 6 были приведены 2 формы одного ОДУ: общая неявная и явная. Если в этих формулах все величины, кроме , считать массивами, то эта же форма записи будет соответствовать системам ОДУ. Следовательно, система ОДУ может быть записана в общем виде

(8.1)

либо в явной форме

(8.2)

где - это независимая переменная, массивы,,,соответствуют вектор-функциям,,,.  Можно записывать также каждое уравнение, используя индексы, тогда получаем

, или

(8.3)

где - номера уравнений и функций,- количество уравнений и определяемых функций. Каждая функцияв правой части (8.3) может зависеть лишь от некоторых функций, но все уравнения должны быть связанными, а иначе это не система, а группа отдельных уравнений, каждое из которых может быть решено с помощью методов, рассмотренных в лекции 6.

При решении одного ОДУ получают одну функцию , а при решении системы ОДУ - массив функций, т.е. каждому значениюсоответствует массивдлины(см. рис.8.1).

Рис.8.1. Решение одного ОДУ и системы ОДУ

Задача Коши. Постановка задачи Коши аналогична случаю одного уравнения (6.2), т. е. должны быть заданы

• функции ,

• отрезок интегрирования ,

• начальные значения для всех функций.

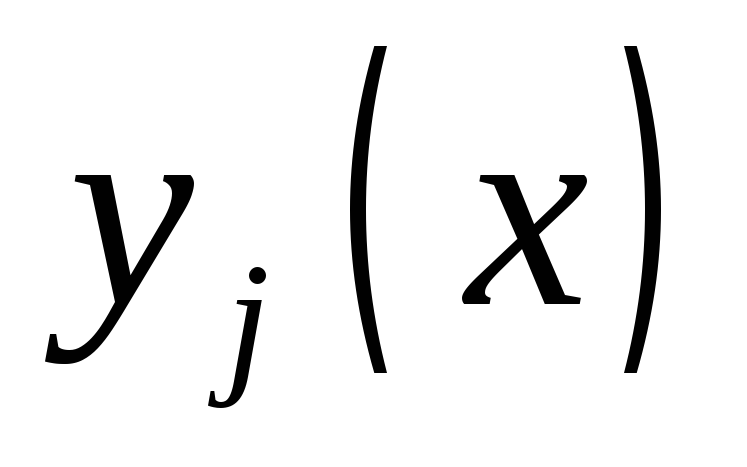Для решения систем ОДУ применяются все методы и все формулы, рассмотренные в лекции 6 для одного ОДУ. Отличие состоит в том, что на каждом шаге вычисляется не одно значение , а массив значений для всех функций (см. рис.8.1). В качестве примера рассмотрим систему двух ОДУ для функцийи

,

c начальными условиями ,. Приводим начало таблицы с расчетами по методу Эйлера (6.3). Пусть шаг дискретизации выбран произвольным и равен. Используются обозначенияидля функций, т.е.,.

0	1	2	2	2	0.1	0.2	0.2
0.1	1.2	2.2	2.3	1.76	0.1	0.23	0.176
0.2	1.43	2.376	и т. д.	...	...	...	...

Из таблицы видим, что изменения производных на шаге велики для метода Эйлера, т.е. шаг выбран слишком крупным и это легко проверить в контрольном расчете с шагом.

Анализ погрешностей и контроль точности аналогичны случаю одного уравнения, см. лекцию 7.

Краевая задача. Кроме задачи Коши, в которой задаются начальные значения всех функций системы (8.3), есть другой большой класс задач, называемых краевыми, в которых значения функций задаются не в одной точке , а в различных точках отрезкадля разных функций. Название "краевые задачи" показывает, что обычно эти дополнительныезначений для (8.4) или (8.6) задаются на краях отрезка, т.е. при и .

Например, для (8.5) получается краевая задача, если задать , .

Методы решения краевых задач основаны на совместном использовании методов решения задачи Коши и методов решения нелинейных уравнений или систем, т.е. краевые задачи сложнее задач Коши. Их идея в следующем. Выбором произвольных начальных значений , , … для всех функций системы решить систему ОДУ, проверить выполнение условий для полученных решений в точке и, используя итерационные методы решения нелинейных уравнений (см. лекцию 5), найти поправки к значениям, , … для следующей итерации, т.е. повторного решения задачи Коши с другими начальными условиями. Итерации прекращаются, когда решение краевой задачи найдено. Этот метод решения краевых задач называют методом "пристрелки".

Для решения краевых задач в MathCAD есть функции sbval, bvalfit.