-
Лекция 6. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
6.1. Применение оду при моделировании.
Пусть
при моделировании определяется функция
,
где каждая переменная может быть скаляром
или массивом, и математическая модель
является дифференциальным уравнением,
т.е. включает производные. Обыкновенные
дифференциальные уравнения (ОДУ) содержат
одну независимую переменную, т.е.
является скаляром, и при этом, если
- скаляр, то имеем одно ОДУ, а для массива
имеем систему ОДУ.
Если
же
- это массив, т.е. независимых переменных
две или более, то производные в уравнении
будут частными, и в отличие от ОДУ такие
уравнения называются уравнениями в
частных производных. В лекциях 6 и 7 будем
рассматривать только одно ОДУ первого
порядка, т.е. уравнение с
.
Отметим, что в задачах моделирования
схем в радиоэлектронике независимой
переменной обычно является время
,
но мы будем использовать для независимой
переменной стандартное обозначение
.
В общем случае одно ОДУ первого порядка имеет вид
|
|
(6.1) |
,Где , например, .
Существует
много уравнений, которые могут быть
решены путем преобразований, и для них
получена аналитическая математическая
модель вида
.
Но для большинства уравнений такое
решение невозможно, и в этих случаях
применяют численные методы. Отметим,
что численные методы дают одно частное
решение (6.1), тогда как аналитические
методы дают решение (6.1) в общем виде.
Пусть
нужно определить функцию
на произвольном отрезке
.
Далее для упрощения записи будем считать
.
Если же это не так, то всегда можно
сделать замену переменных
.
6.2. Задача Коши.
Широкий класс физических задач приводит к ОДУ, разрешенным относительно производной:
|
|
(6.2) |
,
-
произвольная заданная функция двух
переменных. Должно быть также задано
начальное значение функции
в точке
.
Требуется вычислить неизвестную функцию
на отрезке
.
Такая задача называется задачей Коши.
Отметим,
что функция
должна обязательно присутствовать в
правой части (6.2), вместе с
,
если же ее там нет, то уравнение решается
путем численного интегрирования функции
,
рассмотренного в лекции 4.
Если
,
то
,
если
же
,
то
.
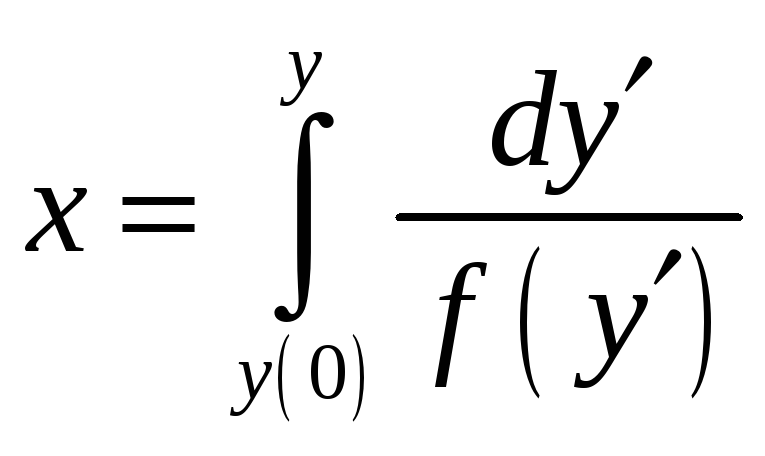Решение
задачи Коши - это получение одного
частного решения
с начальным значением
.
Все методы решения этой задачи основаны
на дискретизации и интерполяции, как и
численное дифференцирование, которое
они используют.
При
дискретизации на отрезке
вводится сетка с узлами
,
.
В простых задачах эта сетка равномерная
и шаг дискретизации равен
.
При вычислениях выполняется цикл по
шагам, т.е. цикл по
,
и на каждом шаге по известному значению
вычисляется следующее значение
с применением интерполяции.
Для
интерполяции функции
на одном или нескольких шагах используются
полиномы степени
.
Например,
для методов Эйлера (явного и неявного),
для метода Рунге-Кутта четвертого
порядка и метода Адамса,
для модифицированного метода Рунге-Кутта
[K1, Ф, К2]. Степень полинома для интерполяции
называют порядком метода.
Если при вычислениях на текущем шаге для интерполяции используются только значения функции на одном этом шаге, то методы решения называются одношаговыми, а если для интерполяции используются также значения с предшествующих шагов, то методы называются многошаговыми. Например, метод Адамса является многошаговым, а остальные из перечисленных выше - одношаговыми.
Следует различать порядок метода и порядок ОДУ, т. к. последний равен порядку старшей производной в уравнении. В последующих разделах будут рассматриваться только ОДУ первого порядка, а ОДУ с производными высших порядков см. в лекции 8.