1.5. Интерполяция полиномами.

1.5.1. Интерполяция с помощью решения слау (системы линейных алгебраических уравнений).

Полином степени

(1.2)

имеет коэффициентов. Если потребовать чтобы он проходил через точек, то получим системулинейных уравнений для:

,

(1.3)

Определитель системы называется определителем Вандермонда:

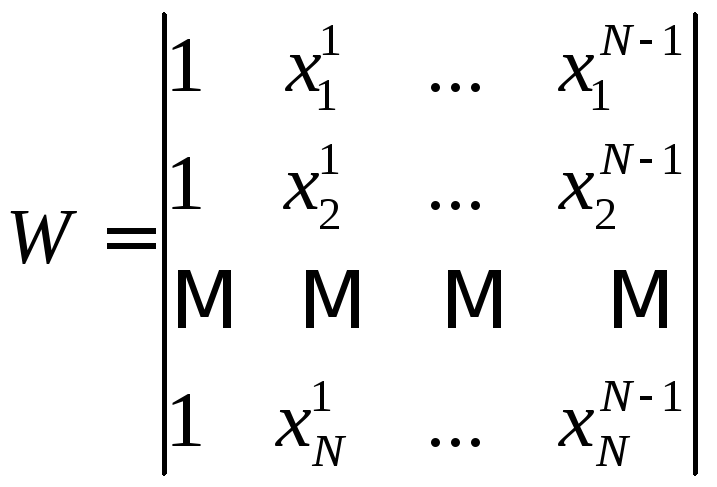
Можно показать, что , еслипри.

Решая систему линейных алгебраических уравнений можно найти . По правилу Крамера, гдеполучается заменой-го столбца вна столбец.

Например для : .

Часто более просто решение СЛАУ получается методом Гаусса или иными методами, рассматриваемыми ниже.

1.5.2. Интерполяция методом Лагранжа.

Используются интерполяционные полиномы Лагранжа

,

(1.4)

для которых

Они имеют степень по, т.к. в числителесомножитель. Следовательно:

(1.5)

есть полином степени , проходящий черезточек. Интерполирующая формула Лагранжа требует большого объема вычислений, для получения более удобного для вычисления вида используют некоторые приемы (например, преобразование к барицентрической формуле, Р.В. Хемминг, «Численные методы», Наука, М. 1972, стр. 104; или использование матриц Д, М.В. Назарова, В.А. Солнцев, Математические методы решения инженерных задач, МИЭМ, М. 1982, стр. 11-12).

Вычисления также упрощаются при равноотстоящих узлах ,. Однако в любом случае, изменяя число точек , надо заново строить полиномы.

1.5.3. Интерполяция методом Ньютона.

При равноотстоящих узлах вместо полиномов Лагранжа удобнее использовать полиномы, получающиеся при построении конечных разностей.

Пусть ,,

Конечные разности последовательности определяются соотношениями

Разности I-го порядка, вычисляются через значение функции в соседних точках;

Разности II-го порядка, вычисляются через разности первого порядка в соседних точках;

Разность -ого порядка.

Конечные разности удобно записывать в виде таблицы:

Согласно методу Ньютона, интерполяционный полином й степени ищется в следующем виде:

(1.6)

Полином должен проходить через все выбранные точек:

; , откуда найдем коэффициентыb_n.

При имеем ;

Для нахождения b₁ составим первую конечную разность, учитывая, что,

Для нахождения составим вторую конечную разность

Продолжая этот процесс, получим:

В результате запишем интерполяционный полином Ньютона -й степени в виде:

(1.7)

;

;

Это первая интерполяционная формула Ньютона. Полином удовлетворяет поставленным условиям.

Докажем, что

и т.д.

При он переходит в отрезок ряда Тейлора, т.к.

При получается формула линейного интерполирование по двум точкам.

При квадратное интерполирование:

Достоинства метода Ньютона:

- вычисления проще;

- можно добавить точки и уточнить интерполяционный полином, не меняя предыдущих вычислений. При увеличении числа точек более чем первыечленов полинома Ньютона не изменяются, только добавляем более новые.

Известны также 2-я интерполяционная формула Ньютона, интерполяционные формулы Гаусса, Стирлинга, Бесселя (см. Демидович, Марон, «Основы вычислительной математики» М. Наука, 1970г.).