Умови виконання роботи

Вихідні дані. Задано нормальні значення сили ваги в трьох точках поверхні нормального земного еліпсоїда.

Таблиця 1

№№ точок	Значення нормальної сили ваги (гали)	Широти (градуси)
1	978,977 + 0,02n	15.3 + 0.3n
2	980,322 + 0,02n	45,4 + 0.3n
3	982,167 + 0,02n	61,6 + 0.3n

Коефіцієнт n задається викладачем для кожного студента і служить для переобчислення табличних вихідних даних у індивідуальні вихідні дані.

Завдання: за заданими значеннями нормальної сили ваги встановити значення полярного стиснення земного еліпсоїда.

Алгоритм розв’язку завдання

1 Перетворюють формулу (1) з урахуванням формули (2) до виду:

На основі цього рівняння складають систему лінійних рівнянь для кожної точки спостереження, приймаючи індивідуальні значення сили ваги у кожній точці за вільний член рівнянь l, позначаючи коефіцієнти літерою в , коефіцієнт – літерою а, значення сили ваги на екваторі – літерою х, а значення сили ваги на полюсі – літерою у. В результаті таких перетворень отримують три лінійні рівняння такого виду:

. (5)

2 На основі трьох лінійних рівнянь виду (5) складають два нормальні рівняння для визначення невідомих значень сили ваги на екваторі (х) і значення сили ваги на полюсі (у)

(6)

3 Розв’язують нормальні рівняння способом визначників і знаходять:

— визначник системи рівнянь

— визначник для невідомого х

— визначник для невідомого y

4 Визначають значення сили ваги на екваторі і на полюсі:

(7)

5 Розраховують допоміжні безрозмірні величини

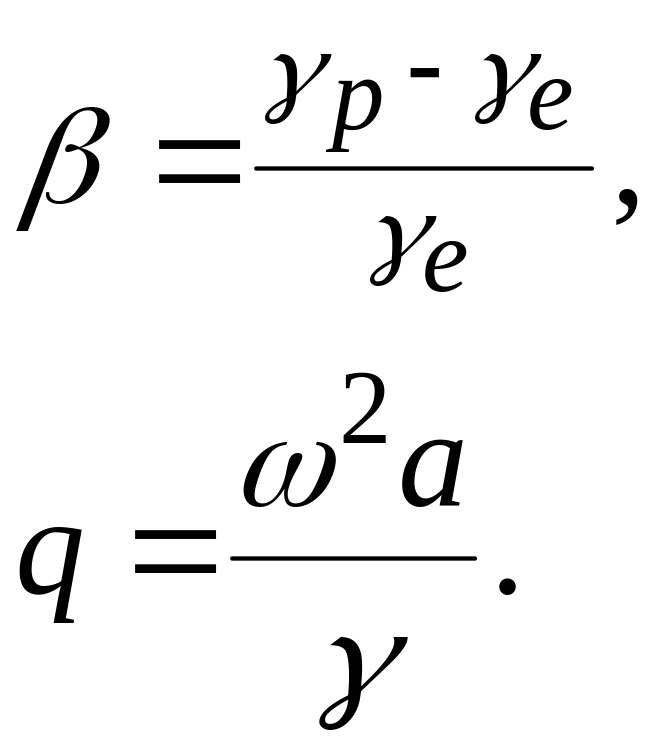(8)

У формулі (8) а = 6378245 і є великою піввіссю референц-еліпсоїда Красовського, а ω – кутова швидкість обертання Землі, яка може бути визначена з формули

6 За формулою Піцетті обчислюють полярне стиснення Землі

(9)

Розраховане значення полярного стиснення Землі приводять до виду .

Контрольні запитання

1 Поняття про фігуру Землі.

2 Сила ваги і її потенціал.

3 Нормальне значення сили ваги. Нормальний еліпсоїд.

4 Одиниці виміру сили ваги.

5 Умови, яким повинен задовольняти нормальний земний еліпсоїд.

6 Формула Клеро для визначення нормального значення сили ваги.

7 Алгоритм визначення полярного стиснення Землі за гравіметричними даними.

8 Формула Піцетті визначення полярного стиснення Землі за гравіметричними даними.

Лабораторна робота № 2 Визначення складових відхилень прямовисних ліній гравіметричним способом

Мета роботи – засвоїти теорію гравіметричного методу визначення складових відхилень прямовисних ліній і методику обчислення цих складових за допомогою карт аномалій сили ваги.

Завдання: в заданій точці місцевості, використовуючи карту аномалій сили ваги, обчислити значення складових відхилень прямовисних ліній.

Тривалість виконання завдання – два заняття.