Основні теоретичні положення

При визначенні висот в гравітаційному полі Землі їх значення повинні задовольняти таким умовам:

1 Висоти пунктів на земній поверхні повинні визначатися однозначно незалежно від шляху нівелювання;

2 Висоти пунктів повинні визначатися лише за даними безпосередніх вимірів на фізичній поверхні Землі без залучення гіпотетичних даних про її внутрішню будову;

3 Для точок одної і тої ж рівневої поверхні висоти точок повинні мати постійне значення.

Умовам 1-3 найкраще відповідає величина, що отримала назву геопотенціалу, і яка визначається формулою

. (37)

В (37) і – значення потенціалу для рівневих поверхонь, що проходять через точки О і М на земній поверхні; g – поточне значення сили ваги вздовж шляху нівелювання; dh – елементарні перевищення між точками вздовж шляху нівелювання (рис. 5).

Якщо точка О є точкою початку обліку висот, тобто співпадає з середнім рівнем моря на задану епоху, то геопотенціал (37) визначає висоту відповідної точки земної поверхні.

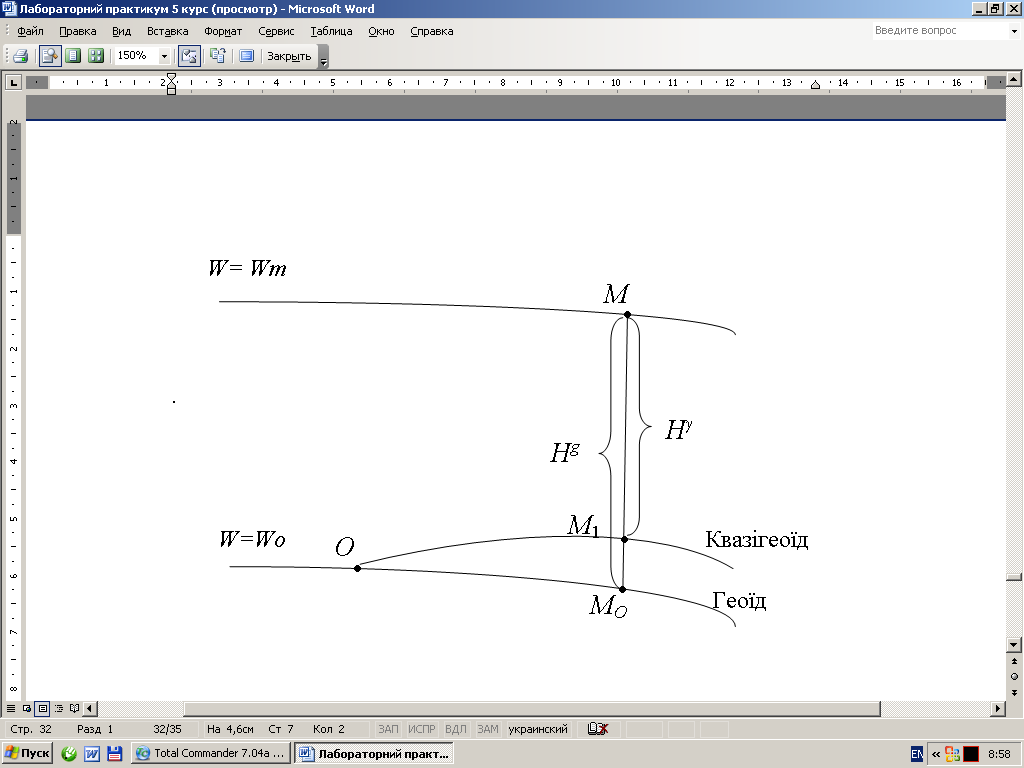
Рисунок 5 – До визначення висот

Висота Н^g, відрахована від точки на земній поверхні по прямовисній лінії до її проекції на геоїді, отримала назву ортометричної висоти. Висота Н^γ, що відрахована від точки на земній поверхні по прямовисній лінії до її проекції на квазігеоїді, отримала назву нормальної висоти.

Відомо, що рівневі поверхні не паралельні між собою. Ця властивість рівневих поверхонь приводить до того, що значення висот точок будуть залежати від шляху нівелювання, а сума перевищень у замкнутому полігоні не буде дорівнювати нулю. В результаті отримують висотну нев’язку, яку назвали теоретичною нев’язкою нівелірного полігону. Значення теоретичної нев’язки обчислюють за формулою:

(38)

У формулі (38) і – значення нормальної сили ваги на поверхні нормального земного еліпсоїда; – середнє значення аномалії сили ваги на тій чи іншій ділянці нівелірного ходу.

Перша складова правої частини формули (38) характеризує вплив непаралельності рівневих поверхонь на результати нівелювання, а друга складова – вплив потенціалу збурення гравітаційного поля Землі на результати нівелювання.

Умови виконання роботи

Вихідні дані.

1 Висоти точок спостереження:

Н_А =1289 м + n м;

Н_В = 686 м + 2n м;

Н_С =1111 м - 3n м.

2 Виміряні перевищення:

h_AB = - 602.784 м + n м;

h_BC = + 425.055 м + 2n м;

h_CA = + 177.729 м - 3n м.

3 Геодезичні широти:

точка А - 55°16′ +5n′;

точка В - 55°20′ +5n′;

точка С - 55°16′ +5n′.

Завдання. Розрахувати значення теоретичної нев’язки нівелір-ного полігону,що утворює трикутник АВС на земній поверхні.

Алгоритм розв’язку завдання

1 Для кожної з точок полігону розраховують значення нормальної сили ваги за формулою Гельмерта:

. (39)

Обчислення виконують з точністю до 0,1 мгал і утворюють різницю цих розрахованих значень .

2 Розраховують середнє значення геодезичної широти для кожної із сторін полігону і за цими значеннями за формулою (39) обчислюють середнє значення нормальної сили ваги .

3 За формулою В.Ф.Еремєєва обчислюють значення нормаль-ної сили ваги для точок прямовисної лінії, розміщених на висоті 0,5Н_m. Маємо:

(40)

4 Для кожної сторони полігону розраховують складову теоретичної нев’язки, яка враховує вплив на результати нівелювання непаралельності рівневих поверхонь, що проходять через кінцеві точки відповідної лінії полігону. Обчислюють:

. (41)

5 В кожній точці нівелірного полігону розраховують за формулою М.І.Юркіної значення аномалії сили ваги. Маємо:

(42)

де – редукція Буге, а коефіцієнт k=2πfδ при середній щільності земної кори δ = 2,67 г/см³ набуває значення k = 0,1118 мгал/м.

6 Визначають редукцію Буге , використовуючи формулу:

(43)

7 Для кожної сторони нівелірного полігону розраховують середнє значення аномалії сили ваги і з цими значеннями обчислюють другу складову теоретичної нев’язки нівелірного полігону, що враховує вплив потенціалу збурення на результати нівелювання. Знаходять:

(44)

8 Розраховують теоретичну нев’язку нівелірного полігону за формулою (38).

9 Розподіляють обчислену нев’язку з оберненим знаком рівномірно на всі перевищення, отримують виправлені значення перевищень і, використовуючи їх, розраховують кінцеві значення нормальних висот полігону.