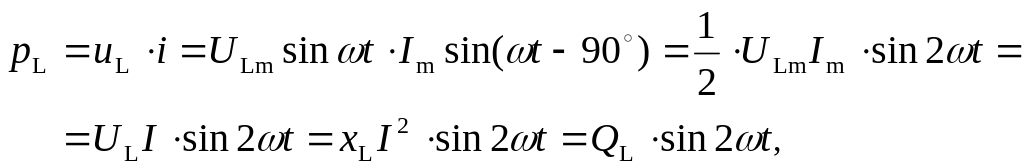Запитання для самоконтролю

1. Опишіть фізичні явища, які спостерігаються в резисторі в колі змінного синусоїдного струму.

2. Складіть розрахункову схему кола з ідеальним генератором і резистором.

3. Запишіть математичний зв'язок між миттєвою напругою, миттєвим струмом і активним опором.

4. Сформулюйте і математично запишіть закон Ома для максимальних і діючих значень напруги і струму на ділянці кола з резистором.

5. Запишіть математичний вираз миттєвої напруги на активному опорі, прийнявши, що початкова фаза дорівнює нулю.

6. Запишіть математичний вираз миттєвого струму в активному опорі для зазначеної вище напруги.

7. Побудуйте графічно оригінали миттєвої напруги і миттєвого струму на ділянці кола з резистором.

8. Зобразіть напругу і струм за допомогою векторів.

9. Що розуміється під кутом зсуву фаз? Чому він дорівнює на ділянці кола з резистором?

10. Отримайте математичний вираз миттєвої потужності в резисторі. З якою частотою коливається миттєва потужність у резисторі?

11. Що розуміється під активною потужністю? Як її розрахувати в резисторі? Укажіть її одиницю.

Завдання для самоконтролю

До резистора підведена напруга u_r = 282 sin (t + 47) В. Активний опір резистора r = 10 Ом.

1. Записати вираз миттєвого струму.

2. Знайти активну потужність у резисторі.

3. Записати вираз миттєвої потужності в резисторі.

4. Зобразити графічно миттєвий струм і миттєву потужність у функції t.

3.3. Коло змінного синусоїдного струму з ідеальною котушкою

Під ідеальною котушкою будемо розуміти таку, у якої активний опір дорівнює нулю. Включимо її в коло з ідеальним генератором синусоїдної е.р.с. (рис.3.12).

Г – генератор синусоїдної е.р.с.;

РА – амперметр;

К – котушка.

С кладемо розрахункову схему кола, нехтуючи опором амперметра і з'єднувальних проводів: генератор виробляє синусоїдну е.р.с., змінний струм у котушці створює змінне магнітне поле (рис.3.13). Буде спостерігатися явище електромагнітної індукції (самоіндукції) і в котушці буде індуктуватися е.р.с. e_L (рис.3.14).

Запишемо рівняння електричної рівноваги кола за другим законом Кірхгофа:

e + eL = 0, e = u, тоді uL = – eL.

(3.33) (3.34)

Е.р.с. самоіндукції, яка наводиться в котушці, залежить від кідькості витків котушки w і швидкості зміни магнітного потоку:

.

(3.35)

З урахуванням (3.1) можемо записати:

.

(3.36)

Підставляємо (3.36) у (3.34) і одержуємо:

.

(3.37)

Отриманий вираз встановлює зв'язок між напругою і струмом в індуктивності.

Задамося струмом у колі

(3.38)

і знайдемо, якою повинна бути напруга на затисках генератора при такому струмі:

де , .

(3.39) (3.40)

Величину L позначимо x_L і назвемо реактивним опором котушки, тобто

xL = L.

(3.41)

Перевіримо одиницю цього опору:

.

Запишемо закон Ома для максимальних значень, виходячи з виразів (3.40) і (3.41) для ділянки кола з індуктивністю:

або або ; .

(3.42) (3.43)

Запишемо закон Ома для діючих значень:

; .	(3.44) (3.45)

Представимо графічно напругу і струм в індуктивності (рис.3.15).

Знайдемо кут зсуву фаз між напругою і струмом в індуктивності:

 = u – i = 0 – (–90) = 90.

Таким чином, струм в індуктивності відстає від напруги за фазою на кут 90.

Знайдемо миттєву потужність в індуктивності:

де .	(3.46) (3.47)

Величину Q_L назвали реактивною потужністю котушки, як одиницю уведено:

QL = вар.

Активна потужність в індуктивності як середнє значення потужності за період:

.

(3.48)

Таким чином, енергія в індуктивності не виділяється у видгляді тепла, а відбувається обмін енергією між джерелом і приймачем.

Розглянемо цей процес на графіку (рис.3.15). У першу чверть періоду, коли струм зростає, збільшується магнітний потік і магнітне поле накопичує енергію (позитивна заштрихована площа), миттєва потужність позитивна і спрямована від джерела до приймача. В другу чверть періоду, коли струм знижується, магнітний потік зменшується і магнітне поле віддає енергію джерелу (негативна заштрихована площа), миттєва потужність негативна і спрямована від приймача до джерела.

Таким чином, миттєва потужність коливається з подвійною частотою – за половину періоду струму миттєва потужність здійснює повне коливання.

Приклад 3.7

До ідеальної котушки підведена напруга u_L = 141 sin (t + 73) В.

Частота струму в мережі дорівнює 50 Гц. Індуктивність котушки дорівнює 12,7 мГн.

Виконати аналіз ділянки кола.

Рішення.

1. Визначаємо індуктивний опір котушки за (3.41):

х_L = 25012,710^–3 = 4 Ом.

2. Визначаємо амплітуду струму за (3.43):

.

3. Визначаємо початкову фазу струму:

_i = _u – 90 = 73 – 90 = –17.

4. Записуємо миттєвий струм:

i = 35,25 sin (t – 17) А.

5. Визначаємо діюче значення струму за (3.14):

.

6. Визначаємо реактивну потужність за (3.47):

Q_L = 425² = 2500 вар = 2,5 квар.