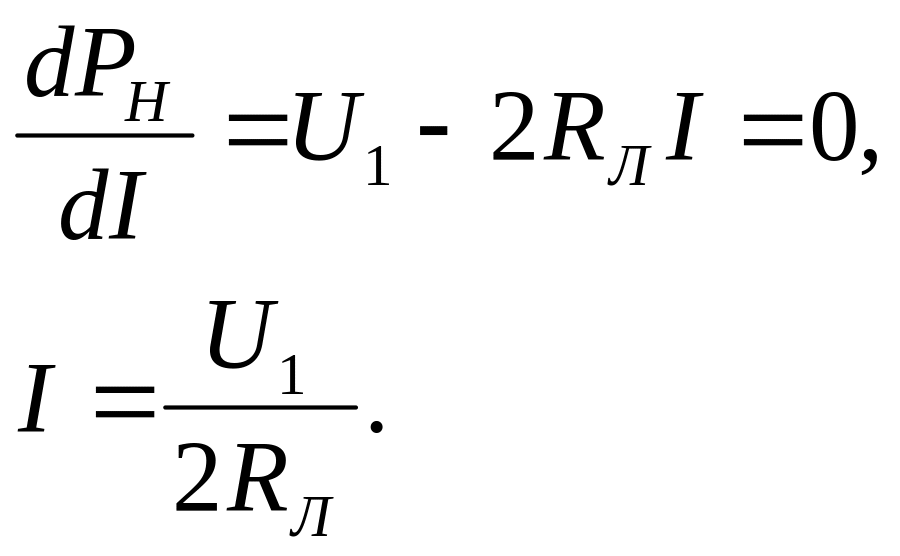1.11. Баланс потужностей

В електричному колі діє закон збереження енергії, відповідно до якого енергія нізвідки не береться і нікуди не зникає, а переходить з одного виду в іншій. Джерело виробляє електричну енергію, перетворюючи, наприклад, механічну енергію.

Запишемо потужність (кількість виробленої енергії за одиницю часу) джерела:

Р = ЕI ,

(1.27)

де Е – е.р.с. джерела, В;

I – сила струму, А;

Р – потужність джерела, Вт.

Р = ВА = Вт .

У проводах, резисторах електрична енергія перетворюється в теплову енергію. Втрати потужності в резисторах (проводах):

Р = RI2 , або P = UI ,

(1.28) (1.29)

де R – опір резистора, Ом;

I – сила струму в резисторі, А;

U – напруга на резисторі, В;

P – втрати потужності в резисторі, Вт.

В електричному колі (рис.1.12) перетворення потужності здійснюється в такий спосіб. Генератор розвиває потужність:

РГ = Е1I .

(1.30)

Ця потужність частково споживається акумулятором і витрачається на його зарядку:

РА = Е2I ,

(1.31)

частково виділяється в акумуляторі та витрачається на нагрівання акумулятора:

Р2 = R2I2 ,

(1.32)

частково виділяється в генераторі та витрачається на його нагрівання:

Р1 = R1I2 ,

(1.33)

частково виділяється в регулюючому реостаті та витрачається на його нагрівання:

Р = RI2 .

(1.34)

Складемо баланс потужностей – рівняння витрати виробленої джерелом (генератором) потужності:

РГ = РА +Р1 + Р + Р2 .

(1.35)

Перепишемо (1.35) в іншому вигляді:

Е1I = Е2I + R1I2 + RI2 + R2I2 ,	(1.36)
або Е1I – Е2I = R1I2 + RI2 + R2I2 .	(1.37)

Запитання для самоконтролю

1. Як скласти баланс потужностей?

1.12. Лінія електропередачі

Дослідимо режим роботи лінії електропередачі постійного струму, прийнявши наступні умови: генератор ідеальний, усі опори лінії покажемо на розрахунковій схемі в одному місці, опір навантаження будемо змінювати від  до 0. Розрахункова схема показана на рис.1.13.

Потужність джерела:

P1 = U1I ; U1 = const .

(1.38)

Потужність, яка споживається навантаженням:

PН = U2I .

(1.39)

Напруга на затисках споживача:

U2 = U1 – RЛI .

(1.40)

Тоді потужність споживача (навантаження):

PН = U1I – RЛI2 .

(1.41)

Знайдемо силу струму, при якій потужність споживача буде максимальною. Для цього візьмемо похідну від Р_н по I і дорівняємо її до нуля:

звідки

(1.42) (1.43)

У загальному випадку сила струму в колі дорівнює:

(1.44)

Порівнявши (1.43) і (1.44) бачимо, що потужність навантаження буде максимальною, якщо

RЛ = RН .

(1.45)

Таким чином, максимальну потужність споживачу можна передати за умови: опір лінії дорівнює опору навантаження. Коефіцієнт корисної дії при цьому буде дорівнювати 50 %, тому що половина потужності, яку розвиває джерело, буде втрачатися в лінії електропередачі.

Приклад 1.15

Для розрахункової схеми, приведеної на рис.1.13, відомо:

Е = 200 В, R_л = 2 Ом, опір навантаження змінюється від 0 до ∞.

Визначити опір навантаження, при якому йому буде передана максимальна потужність, і знайти цю потужність.

Рішення.

Максимальна потужність, яка може бути передана навантаженню, можлива за умови:

R_н = R_л = 2 Ом.

Знаходимо силу струму в колі в цьому випадку:

.

Знаходимо максимальну потужність, яку можна передати навантаженню:

Р_макс = R_н I² = 2  50² = 5 000 Вт = 5 кВт.

Запитання для самоконтролю

1. За якої умови по лінії можна передати навантаженню максимальну потужність? Чому буде дорівнювати к.к.д. лінії у цьому випадку?

21