Задача №8

Определить расстояние от точки С до прямой общего положения (рис.32)

D₅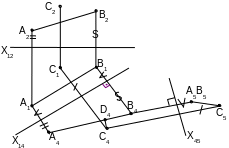

Решение сводится ко 2-й основной задаче. Тогда расстояние по эпюре определяется как расстояние между двумя точками

А₅В₅D₅ и С₅

Проекция С­₄D₄ || Х₄₅

Рис. 32

Задача №9

Определить расстояние от ()D до плоскости, заданной точками А,В,С (рис. 33)

Задача решается как 3-я основная задача. Расстояние Е₄D₄, от ()D₄ до прямой A₄C₄В₄ ,в которую спроецировалась плоскость АВС, является натуральной величиной отрезка ED.

Проекция D­₁E₁ || Х₁₄

Е₂Е_Х12=Е₄ Е_Х14

Построить самостоятельно D­₁E₁

Построить самостоятельно D₂E₂

Рис. 33

Метод вращения вокруг проецирующих прямых

(к задаче №10)

При вращении точки вокруг проецирующей прямой с её проекциями происходит следующее: проекция точки на плоскость, к которой перпендикулярна ось вращения, перемещается по окружности, в то время, как другая проекция точки перемещается по прямой, параллельной соответствующей оси проекций.

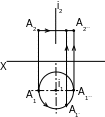
На рис.34 i – ось вращения  ₁.

Горизонтальная проекция траектории

движения точки – окружность с центром в () i₁, фронтальная – || оси Х.

Рис.34

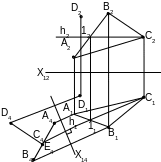
Углы наклона прямой общего положения к плоскостям проекций (задача 10) определяются через нахождение натуральной величины отрезка, принадлежащего этой прямой (1-я основная задача) (рис.35).

Рис.35

Чтобы найти угол  наклона прямой к плоскости ₁, необходимо провести ось i  ₁, через какую-либо точку (В) и вращать отрезок вокруг этой оси до положения || ₂. Тогда точка В останется неподвижной, В₁А₁ || оси Х; В₂А₂ –Н.В.[АВ];  – искомый.

Аналогично, вращая АВ вокруг оси j  ₂ до положения || ₁ , можно найти  – угол наклона прямой к ₂.

Метод плоскопараллельного перемещения

(к задачам №11,12)

Плоскопараллельным называется перемещение всех точек геометрической фигуры по плоским траекториям, параллельным одной из плоскостей проекций, без указания оси вращения.

Фигура в пространстве перемещается до тех пор, пока задача ни будет решена или ни упростится её решение. При этом проекция фигуры на плоскость, параллельно которой происходит перемещение, не меняет своих размеров и формы, меняется только её положение. В то же время другие проекции её характерных точек перемещается по прямым, параллельным соответствующей оси проекций.

Определение натуральной величины плоской фигуры (задача №11) сводится к решению 4-й основной задачи (рис. 36).

Рис.36

1. Преобразовать плоскость АВС в проецирующее положение:

h₁ Х; B₂A₂C₂ – прямая линия.

2. Преобразовать плоскость АВС в положение плоскости уровня:

B₂A₂C₂ || Х; B₁A₁C₁– Н.В.

Определение величины двугранного угла (задача №12) сводится к решению 2-й основной задачи (рис.37).

Преобразовать ребро АВ в положение уровня: A2B2 || Х. Преобразовать ребро АВ в проецирующее положение: A1B1  Х;  – искомый линейный угол, которым измеряется величина двугранного угла.

Рис.37