Теорема о перпендикулярности прямой и плоскости

Чтобы прямая в пространстве была  плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была  горизонтальной проекции горизонтали, а фронтальная проекция – к фронтальной проекции фронтали этой плоскости.

Задача №5 (рис.23)

Построить плоскость  заданной и удаленную от неё на 30 мм.

План:

1. Из () А плоскости восставить перпендикуляр;

2. На прямой l от () А отложить 30 мм = () S;

3. Через () S провести плоскость, параллельную заданной.

Рассмотрим этапы этой задачи:

1.Из () А плоскости восставить  к плоскости АВС (рис. 21), используя теорему о перпендикулярности.

П лан:

1) В плоскости АВС провести горизонталь и фронталь.

h₂ || X₁₂ h₁

f₁ || X₁₂  f₂

2) Через () А (А₁,А₂) провести проекции перпендикуляра l (l₁,l₂)

l₁  h₁; l₂  f₂

Рис.21

2.На прямой l от ()А отложить 30 мм (рис. 22).

План:

1)На прямой l выбрать произвольную

()K (К₁,К₂);

2) Найти н.в. величину отрезка [АK];

3) На н.в. [АK] от ()А отложить 30 мм,

получить()S;

4) Через ()S провести  к l₁  S₁

и по линии связи S₂.

Рис. 22

Д ве плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

n ll AC

m ll AB

Рис. 23

Определение расстояния от точки до плоскости (рис. 24) (к задаче №6)

План:

1. Из точки D опустить перпендикуляр на плоскость (для этого в плоскости проводят h,f);

2. Найти точку K пересечения прямой с плоскостью (см. рис.20);

3. Н айти н.в. отрезка перпендикуляра DK (см. рис.8).

Определение расстояния от точки до прямой общего положения (рис. 25)

( к задаче №7)

План:

1. Через точку A провести плоскость , перпендикулярную к прямой l (плоскость  задают пересекающимися горизонталью h и фронталью f);

2. Найти точку K пересечения заданной прямой l с построенной плоскостью;

3. Найти н.в. отрезка перпендикуляра AK.

1) h  l; f  l; A  h; A  f; 2)  (h,f)  l = K 3) Н.В.[АК] – искомое расстояние от () А до прямой l

Рис. 25

Контрольная работа №2

Большинство метрических задач начертательной геометрии решается с применением методов преобразования проекций, так как они позволяют преобразовать исходные данные в такое положение, которое упрощает решение задачи. Преобразования, как правило, сводятся к четырем основным задачам:

1. Преобразование прямой общего положения в прямую уровня;

2. Преобразование прямой общего положения в проецирующую прямую;

3. Преобразование плоскости общего положения в проецирующую плоскость;

4. Преобразование плоскости общего положения в плоскость уровня.

Метод замены плоскостей проекций (к задачам №8, 9)

Данную геометрическую фигуру оставляют в системе плоскостей проекций неподвижной. Новые плоскости проекции устанавливают так, чтобы получаемые на них проекции обеспечивали рациональное решение рассматриваемой задачи. При этом каждая новая система плоскостей проекций должна быть системой ортогональной. После проецирования объектов на плоскости они совмещаются в одну посредством вращения их вокруг общих прямых (осей проекций) каждой пары взаимоперпендикулярных плоскостей.

Т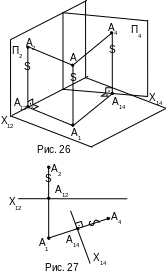 ак, например, пусть в системе двух плоскостей П₁ и П₂ задана точка А. Дополним систему еще одной плоскостью П₄ (рис. 26), П₁П₄. Она имеет общую линию Х₁₄ с плоскостью П₁. Строим проекцию А₄ на П₄.

АА₁=А₂А₁₂=А₄А₁₄

На рис. 27, где плоскости П₁, П₂ и П₄ приведены в совмещение, этот факт определен результатом А₁А₄Х₁₄, а А₁₄А₄А₂А_12.

Правило:

Расстояние новой проекции точки до новой оси проекции (А₄А₁₄) равно расстоянию от заменяемой проекции точки до заменяемой оси (А₂А₁₂).

На примере метода замены плоскостей проекций рассмотрим решение всех основных задач.

1-я основная задача:

В₂

Преобразование прямой общего положения в прямую уровня (рис.28):

а) П₄ || АВ (ось Х₁₄ || А₁В₁)

б) А₁А₄Х₁₄; В₁В₄Х₁₄

в) А₄А₁₄=А₁₂А₂

В₄В₁₄=В₁₂В₂

А₄В₄ = н.в.

Рис. 28

2-я основная задача:

Преобразование прямой общего положения в проецирующую (рис.29):

а ) П₄ || АВ (Х₁₄ || А₁В₁)

А₁А₄Х₁₄

В₁В₄Х₁₄

А₁₄А₄=А₁₂А₂

В₁₄В₄=В₁₂В₂

А₄В₄ - н.в.

б) П₅АВ (Х₄₅А₄В₄)

А₄А₅Х₄₅

В₄В₅Х₄₅

А₄₅А₅=В₄₅В₅=А₁₄А₁=В₁₄В₁

А₅В₅

Рис. 29

3-я основная задача:

В₂

Преобразование плоскости общего положения в проецирующее положение (рис.30):

Плоскость можно привести в проецирующее положение, если одну прямую плоскости сделать проецирующей. В плоскости АВС проведем горизонталь (h₂, h₁), которую за одно преобразование можно сделать проецирующей. Проведем плоскость П₄ перпендикулярно горизонтали; на эту плоскость она спроецируется точкой, а плоскость треугольника – прямой линией.

Рис. 30

4-я основная задача:

Преобразование плоскости общего положения в плоскость уровня (рис.31):

Плоскость сделать плоскостью уровня с помощью двух преобразований. Вначале плоскость надо сделать проецирующей (см. рис. 30) а затем провести П₅ || А₄В₄С₄, получим А₅В₅С₅ - н.в.

Рис. 31