Решение:

Чтобы закодировать 65536 различных цветов для каждой точки, необходимо 16 бит. Чтобы закодировать 16 цветов, необходимо всего 4 бита. Следовательно, объем занимаемой памяти уменьшился в 16:4=4 раза.

Задача. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея- 800 х 600 пикселей? ([6], №63)

Решение:

1. Найдем объем видеопамяти для одной страницы: 800*600*24=11520000 бит =1440000 байт =1406,25 Кб ≈1, 37 Мб

2. 1,37*4 =5,48 Мб ≈5.5 Мб для хранения 4 страниц.

Задача. Сканируется цветное изображение стандартного размера А4 (21х29.7 см). Разрешающая способность сканера 1200 dpi, глубина цвета 24 бита. Какой информационный объем будет иметь полученный графический файл?

Решение.

1. Переведем разрешающую способность сканера из точек на дюйм в точки на сантиметр: 1200 dpi/2,54 = 472 точек/см

2. Размер изображения в точках составит: 472*21 х 472*29,7 = 9912х14018 точек

3. Общее количество точек сканера: 9912х14018=138946416

4. Информационный объем файла равен:

24*138946416= 397,5 Мб

Временная дискретизация звука

A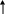 (t)

t

Рисунок 1. Временная дискретизация звука.

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче, чем больше частота, тем выше тон. Для того, чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).

В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. При этом звуковая волна разбивается на мелкие временные участки, для каждого из которых устанавливается значение амплитуды. На графике это выглядит как замена гладкой кривой на последовательность ”ступенек”, каждой из которых присваивается значение уровня громкости. Чем большее количество уровней громкости будет выделено в процессе кодирования, тем более качественным будет звучание.

Современные звуковые карты обеспечивают 16-битную глубину кодировки звука. Количество различных уровней сигнала можно рассчитать по формуле: N=2¹⁶=65536. Т.о., современные звуковые карты обеспечивают кодирование 65536 уровней сигнала. Каждому значению амплитуды присваивается 16-ти битный код.

При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т.е. частотой дискретизации. Чем большее количество измерений проводится в 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.

Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации.

Частота дискретизации - это количество измерений громкости звука за одну секунду (1/Период (герц)). Период измерений - промежуток времени между двумя измерениями.

Разрядность регистра звуковой карты определяется формулой:

2i=N

где i – разрядность регистра (разрядность дискретизации),

N – количество уровней измерения звука.

Частота дискретизации аналогового звукового сигнала может принимать значения от 8 кГц до 48 кГц. При частоте 8 кГц качество дискретизованного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD. Следует также учитывать, что возможны как моно-, так и стереорежимы.

Задача. Попробуем оценить информационный объем стереоаудиофайла длительностью звучания 1 секунда при высоком качестве звука (разрядность дискретизации -16 бит, частота дискретизации - 48 кГц). Для этого количество битов нужно умножить на количество выборок в 1 секунду и умножить на 2 (стерео):

16 бит*48 000 *2 = 1 536 000 бит = 192 000 байт = 187,5 Кбайт

Уровень громкости звука можно рассматривать как набор возможных состояний N, для кодирования которых необходимо определенное количество информации I, которое называется глубиной кодирования звука.

Глубина кодирования звука – это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.

2i=N

где: N – уровни громкости звука;

i – глубина кодирования звука.

Пусть глубина кодирования звука составляет 16 битов, тогда количество уровней громкости равно: N = 2ⁱ = 2¹⁶ = 65536

Информационный объем (количество информации)= глубина звука (разрядность дискретизации)*частота дискретизации