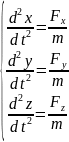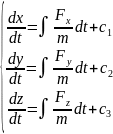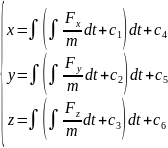- •4. Связи и реакции связей. Принцип освобождаемости от связей. Виды связей.
- •6. Проекции силы на оси координат.
- •14. Опоры и опорные реакции балок. Распределённые нагрузки
- •19. .Расчет сост.Конструкций. Статистически неопределимые системы.
- •20. Расчет плоских ферм. Клас. Ферм.Методы расчета плоских ферм.
- •23. Центр параллельных сил. Центр тяжести.
- •24)Кинематика.Основные определения.Способы задания точки.
- •25. Виды движения точки в зависимости от ускорений. Равномерное движение. Неравномерное и равнопеременное движение.
- •26. Простейшие движения твёрдого тела. Поступательное движение. Вращательное движение. Виды вр-ого дв.
- •29. Основны кинетостатики. Принцип Даламбера. Работа силы. Мощность силы.
25. Виды движения точки в зависимости от ускорений. Равномерное движение. Неравномерное и равнопеременное движение.
В зависимости от касс-го и норм-го ускорения:
1)
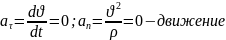 прямолинейное
и равномерное (
прямолинейное
и равномерное (
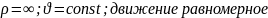 )
)
2)
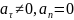 – движение прямолинейное, неравномерное
– движение прямолинейное, неравномерное
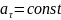 -
движение равнопеременное
(равноускоренное,равнозамедленное)
-
движение равнопеременное
(равноускоренное,равнозамедленное)
3)
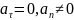 – криволинейное, равномерное
– криволинейное, равномерное
 При
движении по кривой всегда присутствует
норм-е ускорение.
При
движении по кривой всегда присутствует
норм-е ускорение.
4)
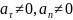 криволинейное,
неравномерное
криволинейное,
неравномерное
Равномерное и равнопеременное движение:
Уравнение равномерного движения:
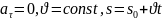
При равнопеременном движении:
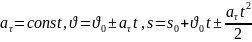 ,
где
,
где
 -
нач-я скорость, ”+” при равноускоренном
движении, ”-” при равнозамедленном.
-
нач-я скорость, ”+” при равноускоренном
движении, ”-” при равнозамедленном.
26. Простейшие движения твёрдого тела. Поступательное движение. Вращательное движение. Виды вр-ого дв.
Различают 5 видов движения твёрдого тела:поступательное (простейшее),вращательное (простейшее), плоско-параллельное (плоское),сферическое,общий случай движения (сложное
Поступательным называется такое движение при котором любая прямая, принадлежащая телу, движется параллельно самой себе.Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют геометрически равные скорости и ускорения.
Вращательным наз-ся такое движение, при котором сущ-ет прямая, принадлежащая телу и остающаяся неподвижной в процессе всего движения. Основные харак-ки вращ-го дв-я:
угловая координата (закон движения)
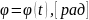 -
пок-ет изм-е положения тела с течением
времени.
-
пок-ет изм-е положения тела с течением
времени.
угловая скорость
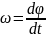 -
первая производная оси угловой координаты
-
первая производная оси угловой координаты
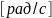 -
пок-ет быстроту изменения угловой
координаты
-
пок-ет быстроту изменения угловой
координаты
угловое ускорение
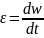 -
первая производная от угловой скорости
-
первая производная от угловой скорости
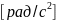 -
пок-ет быстроту изм-я угловой скорости
-
пок-ет быстроту изм-я угловой скорости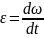
Если
знаки
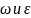 совпадают,
то их напр-я также совпадают и вращение
тела ускоренное и наоборот.
совпадают,
то их напр-я также совпадают и вращение
тела ускоренное и наоборот.
Равномерное и равнопеременное вращение:
Равномерным
наз-т вращение при кот.
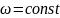 , т.е. нет углового ускорения.
, т.е. нет углового ускорения.
Ур-е
равномерного вращения:
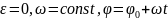 , где
, где
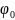 -
нач-я координата.
-
нач-я координата.
Равнопеременным
наз-ся вращение с постоянным угловым
ускорением:
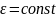 .
.
Ур-я
равнопеременного вращения:
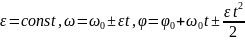
“+” – равноускоренное движение, “-” – равнозамедленно.
27. . Динамика: основные понятия и определения. Законы динамики. Задачи динамики.
Динамика – раздел теор-й мех-ки, изучающий законы движения точек или тел с учётом причин, вызывающих это движение. Динамика состоит из 2 частей: 1) динамика матер-ой точки; 2) динамика мех-ой системы.
Матер-я точка – тело, имеющее массу размерами которого в данной системе отсчёта можно пренебречь.
Мех-я система – сов-ть матер-х точек или тел.
Законы динамики:
1 закон динамики: всякое тело сохраняет своё равновесное сост-ие до тех пор пока другие тела не выведут его из этого со состояния. Такая способность тела наз-ся инерцией .Поэтому первый закон динамики – закон инерции. Системы отсчёта, отн-но кот. справедлив закон инерции наз-ся инерциальными (они должны быть неподвижными). Система отсчёта связанная с Землёй считается условно неподвижной. Пример инерциальной системы отсчёта – гелиоцентрическая система координат.
2
закон
(основной закон динамики): ускорение,
сообщаемое матер-ой точке силой прямо
пропорциональных величин этой силы
совпадает с ней по направлению.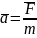 .
.
3 закон (принцип рав-ва действия и противодействия): силы взаимод-я между собой двух тел равны по величине и направлены по одной прямой в противоположные стороны.
4
закон
динамики (закон независимости действия
сил): ускорение, кот. получает матер-я
точка от действия равнодействующей
силы равно векторной сумме ускорения,
кот. получила бы точка от действия каждой
из состав-щих сил в отд-сти.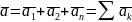 . Исходя из этого основной закон динамики
можно записать в виде:
. Исходя из этого основной закон динамики
можно записать в виде:
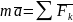 , где
, где
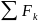 геом-ая сумма прил-ых к точке сил.
геом-ая сумма прил-ых к точке сил.
Две задачи динамики точки:
1 задача (прямая): по заданным ур-иям движения опред-ся силы, действующие на точку.
2 задача (обратная): по известным массе точки , усл. движения и действующей силе опр-ть ур-е движения.
28. Основные уравнения движения материальной точки. Решение первой и второй задачи динамики.
Дифференциальные уравнения (ДУ) движения точки (в векторной форме):
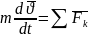 или
или
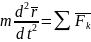
ДУ движения точки в декартовых осях координат:
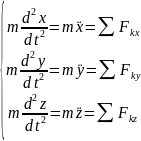
Можно
записать эти ур-я в естественных осях
координат (подвижных).
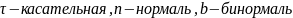
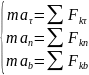

ДУ движения точки в естественных осях координат:

Решение первой и второй задачи динамики:
1 задача (прямая): по заданным уравнениям движения определяются силы, действующие на точку.
Общий
пример: дано:
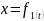 ,
y
,
y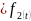 ,
,
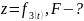 . Решение: находим вторые производные:
. Решение: находим вторые производные:
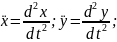
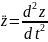
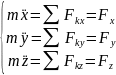 где
где
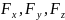 – проекции силы на оси координат
– проекции силы на оси координат
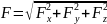
2 задача (обратная): по известным массе точки , усл. движения и действующей силе опр-ть ур-е движения.
Общий
пример: дано m,
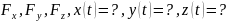 .
Решение:
.
Решение: