2) Масса системы. Центр масс.

Механическая система – это система материальных точек, каждая из которых имеет определенную массу и занимает в данный момент времени определенное положение в пространстве.

Для удобства решения задач динамики механические системы желательно некоторые обобщенные (т.е. суммарные ) характеристики, которые бы отражали и массу системы, и ее «геометрию масс», т.е. расположение в пространстве материальных точек системы.

Масса системы М равна арифметической сумме масс всех точек или тел, образующих систему:

Центром масс механической системы называют геометрическую точку С, радиус вектор которой

(1)

где радиус- вектор точек, образующих систему.

- массы точек механической системы

М – масса системы.

Центр масс системы явл не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы. Центр масс системы характеризует распределение масс в системе.

Теорема о движении центра масс механической системы.

Теорема: Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все действующие на систему внешние силы.

(3)

Где - ускорение центра масс.

- главный вектор внешних сил.

Проецируя обе части уравнения на координатные оси, получим:

где , , - координаты центра масс.

Из теоремы о движения центра масс можно получить следующие важные следствия, которые выражают закон сохранения центра масс механической системы.

Если геометрическая система всех внешних сил, действующих на систему, равна 0 () то это значит , что или , т.е. центр масс этой системы движется с постоянной по модулю и направлению скоростью (иначе, равномерно и прямолинейно). В частном случае, если вначале центр масс был в покое () то он и останется в покое т.е ().

Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, ось Х равна 0 , то или т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. В частном случае , если в начальный момент , то и в любой последующий момент времени это значение сохранится , а следовательно координата центра масс системы не изменится т.е. = const.

Теоремы об изменении количества движения точки и системы

Определение: количеством движения материальной точки называется векторная величина ,равная произведению массы точки на вектор ее скорости. Вектор приложен к движущейся точке.

Определение: Количеством движения механической системы называется вектор, равный геометрической сумме количеств движения всех точек системы.

(4)

Вектор является свободным вектором. Как правило скорости всех точек системы различны и поэтому непосредственное суммирование векторов в правой части равенства является затруднительным.

Воспользуемся формулой для определения центра масс механической системы (1)

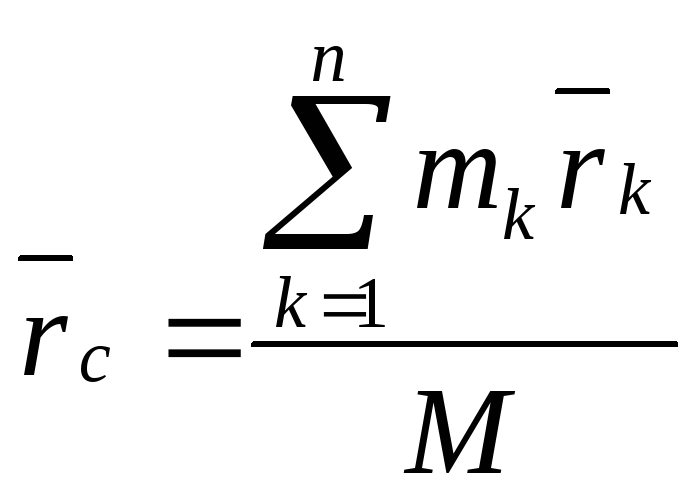
Или запишем в виде

дифференциируя обе части выражения по времени получим:

или

(5)

Сравнивая формулы (4) и (5) получим , что количество движения системы равно произведению массы всей системы на скорость ее центра масс.

(6)

Вектор является обобщенной векторной характеристикой движения всей механической системы. В общем случае движение системы ее количество движения можно рассматривать как характеристику поступательной части движения системы вместе с центром масс. Если при движении системы (тела) центр масс неподвижен, то количество движения будет равно 0. Например количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс.

Запишем второй закон динамики для материальной точки: учитывая что получим (7)

В каждый момент времени производная по времени от количества движения точки равна действующей на точку силе.

Если обе части равенства (7) умножить на dt, то получим векторная величина, стоящая в правой части этого равенства, характеризует действие, оказываемое на тело силой за элементарный промежуток времени dt эту величину называют элементарным импульсом силы , т.е.

(8)

Импульс силы за конечный промежуток времени t₂ – t₁ равен

(10)

Уравнение (10) выражает теорему об изменении количества движения точки в конечной интегральной форме:

Теорема: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы ( или равнодействующей всех приложенных к ней сил)за тот же промежуток времени.

При решении задач пользуются уравнениями этой теоремы в проекциях на координатные оси.

Рассмотрим механическую систему, состоящую из n материальных точек. Тогда для каждой точки можно применить теорему об изменении количества движения в дифференциальной форме:

( k = 1, 2….n).

Суммируя эти равенства, получим

т.к. по свойству внутренних сил

то получим:

(11)

Уравнение (11) выражает теорему об изменении количества движения системы в дифференциальной форме:

Теорема: Производная по времени от количества движения системы равна векторной сумме действующих на систему внешних сил.

В проекциях на координатные оси:

; ;

Умножая обе части равенства (11) на dt и интегрируя, получим:

(12)

Уравнение (12) выражает теорему об зменении количества движения системы в интегральной форме:

Теорема: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему за то же время.

Из теоремы об изменении количества движения системы можно получить следующие важные следствия, которые выражают закон сохранения количества движения системы.

1. Если геометрическая сумма всех внешних сил, действующих на систему, равна 0 (), то значит, что при этом , т.е. вектор количества движения системы будет постоянен по модулю и направлению.

2. Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-либо ось равна 0, то значит .