Лекции 3, 4

Тема 3 неразветвЛёННые электричесКие цеПи переменного синусоидального тока

3.1. Основные физические понятия

Явление электромагнетизма было открыто в 1820 году датским физиком Г.Х. Эрстедом, суть которого состоит в том, что при протекании по проводнику элек­трического тока вокруг последнего образуется магнитное поле.

Был установлен закон электромагнетизма: потокосцепление электриче­ской катушки прямо пропорционально силе электрического тока и индук­тивности ка­тушки.

Математическая запись закона электромагнетизма следующая:

,

(3.1)

где  – потокосцепление катушки, Вб;

Ф – число витков катушки;

L – индуктивность катушки, Гн;

i – сила электрического тока в катушке, А.

Представим описанное явление схематически (рис.3.1).

Я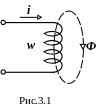 вление электромагнитной индукции открыл в 1831 году английский физик Майкл Фарадей, суть которого состоит в следующем: если проводящий контур пронизы­вается пере­менным магнитным потоком, то в контуре индуктируется (наводится) электродвижущая сила.

Закон электромагнитной индукции: значение электродвижущей силы, наводимой в контуре, прямо пропорционально числу вит­ков контура и скорости изменения магнит­ного потока.

Математическая запись закона:

,

(3.2)

где е – электродвижущая сила, В;

w – число витков катушки;

Ф – магнитный поток, Вб;

t – текущее время, с.

.

Пример 3.1

Катушка, состоящая из 100 витков, имеет индуктивность 0,1 Гн;

по катушке протекает ток i = 10 sin t А.

Определить магнитный поток внутри катушки.

Решение.

Из (3.1) находим магнитный поток:

. (3.1а)

Подставляем значения физических величин и получаем:

.

Физический смысл знака «минус» состоит в следующем: если в данный мо­мент времени магнитный поток, пронизывающий контур, увеличивается, то он наводит э.д.с., которая создаст электрический ток, а последний свой маг­нитный поток, ко­торый будет направлен против основного потока и наобо­рот.

Р ассмотрим это на графике (рис.3.2).

Явления электромагнетизма и электро­магнитной индукции лежат в основе прин­ципа действия генераторов переменного си­нусоидального тока.

Приведём вариант конструктивной схемы генератора переменного синусои­дального тока (рис.3.3).

М агнитный поток создается током на­магничивания I. Проводящий контур (рамка) помещается на оси между полюсами электромагнита. Если рамку привести во вращение, то магнитный поток, пронизы­вающий рамку, будет изменяться во вре­мени по синусоидальному закону и в рамке будет наводиться э.д.с., которая также будет изменяться по синусоидальному закону в зависимости от угла отклонения рамки от горизонтального положения (рис.3.2, 3.3), т.е.

е = Em  sin,

(3.3)

где Е_m – амплитудное (максимальное)

зна­чение э.д.с. (при вертикальном

поло­жении рамки), В;

 – угол отклонения рамки

от гори­зонтального положения, рад (град);

e – мгновенное значение э.д.с. для за­данного угла отклонения рамки, В.

Угол отклонения рамки зависит во вре­мени от угловой скорости вращения рамки:

 =   t,

(3.4)

где  – угловая скорость вращения рамки, рад/с (град/с);

t – текущее время, с.

Таким образом, подставив (3.4) в (3.3), получим зависимость э.д.с. от угловой скорости вращения рамки:

е = Em  sin t,

(3.5)

Пример 3.2

Катушка индуктивности, состоящая из 100 витков, пронизывается магнитным потоком ф = 0,01 sin t Вб,  = 314 с^–1 .

Определить электродвижущую силу, которая наводится в катушке.

Решение.

Подставляем значения физических величин в (3.2) и получаем:

.

Если рамку замкнуть с помощью щёточного механизма на резистор, то воз­никает синусоидальный ток:

i = Im  sin t,

(3.6)

где I_m – амплитудное (максимальное) значение тока

(при амплитудном значении э.д.с.), А;

i – мгновенное значение тока, А.

Покажем график i = f(t) на рис.3.4.

З апишем угловую скорость вращения рамки через частоту (количество оборотов в секунду):

 = 2f,

(3.7)

где f – частота вращения рамки, (1/с) Гц.

С такой же частотой f будет изменяться и электрический ток.

Время одного оборота рамки обозначим через Т; таким же будет и время одного пол­ного колебания тока, назовём его периодом тока.

В Европе частота тока равна 50 Гц, т.е. f = 50 Гц (1/с).

Тогда период тока Т = 0,02 с, т.е.

.

(3.8)

В общем случае в момент времени t = 0 рамка может находиться под опреде­лённым углом по отношению к горизонтальному положению и тогда мгновенное значение тока записывается следующим образом:

i = Im  sin( t + i),

(3.9)

где _i – начальная фаза тока (начальный угол отклонения рамки), рад (град);

( t+ _i) – текущая фаза тока, рад (град).

С инусоидальные величины (токи, напряжения, э.д.с., потенциалы) изобра­жают на плоскости с помощью векторов. Для этого берётся амплитудное значение синусоидальной величины и в выбранном масштабе откладывается в виде отрезка прямой под углом к оси отсчёта, равным начальной фазе изображаемой величины. Если начальная фаза положительная, то угол отсчёта откладывается против часо­вой стрелки, если отрицательная – по часовой стрелке. В качестве примера ток i = I_m  sin( t+ 45) А изображён на рис.3.5.

Угловую скорость вращения рамки называют круговой (угловой) частотой тока:

 = 2f = 250 = 314 рад/с

и график i = f ( t ) чаще всего строят в виде i = f ( t ), т.е. мгновенное значение тока в функции мгновенного значения фазы тока (мгновенного угла поворота рамки).

В виде вектора ток изображают для момента времени t = 0. Мгновенное зна­чение тока в любой другой момент времени (другой фазы тока) есть проекция вектора на вертикальную ось (рис.3.5).

Пример 3.3

По катушке протекает ток i = 15 sin (t + 30) А.

Изобразить ток в виде вектора.

Р ешение.

Выбираем масштаб тока m_i = 0,5 А/мм и строим вектор тока (рис.3.6).

Сопротивление проводника переменному току (активное) зависит от частоты тока и связано с тем, что в результате вытеснения тока на поверхность провод­ника сечение проводника как бы уменьшается, что приводит к увеличению его сопро­тивления по сравнению с постоянным током. Вытеснение тока на поверхность проводника (поверхностный эффект) объясняется явлением электромагнитной индукции. Переменное магнитное поле вокруг проводника, созданное перемен­ным током в проводнике, наводит э.д.с. самоиндукции. Если представить провод­ник состоящим из множества параллельных нитей, по которым проходят свои токи, то самое большое число магнитных силовых линий сцеплено с централь­ными нитями и там наводится самая большая э.д.с., которая препятствует току и вытесняет его на поверхность (рис.3.7).

И зображается активное сопротивление на расчётных схемах следующим образом: .

Из курса физики известно, что индуктивность катушки (проводника) зависит от квадрата числа витков, магнитной проницаемости среды, по которой замыкается магнитный поток, площади внутреннего сечения катушки и длины средней силовой линии магнитного потока, т.е.

,

(3.10)

где w – число витков катушки;

 – относительная магнитная проницаемость среды,

по которой замыкается магнитный поток;

₀ – магнитная постоянная (₀ = 410^–7 Гн/м), Гн/м;

S – площадь внутреннего сечения катушки, м²;

l – длина средней магнитной силовой линии, м.

.

И ндуктивность на расчётных схемах изображается следующим образом:

.

Пример 3.4

Катушка индуктивности без ферромагнитного сердечника имеет 1000 витков. Площадь внутреннего сечения катушки равна 400 см², длина средней силовой линии магнитного потока катушки равна 12,56 см.

Определить индуктивность катушки.

Решение.

Подставляем значения параметров катушки в (3.10) и получаем:

.

Действующее значение переменного синусоидального тока. Переменный синусоидальный ток, проходя по проводнику, сопровождается тепловым дейст­вием независимо от направления тока. Мгновенная мощность, выделяемая в про­воднике

р = ri2,

(3.11)

где r – активное сопротивление, Ом;

i – мгновенный ток, А;

р – мгновенная мощность, Вт.

Найдём количество тепла (энергии), которое выделится в проводнике за пе­риод тока:

.

(3.12)

Заменим действительный переменный синусоидальный ток эквивалентным постоянным током, при котором за период выделится такое же количество тепла в том же проводнике:

W = rI2T,

(3.13)

где I – эквивалентный постоянный ток, А.

Приравняв (3.12) с (3.13), находим:

.

(3.14)

Величину эквивалентного постоянного тока назвали действующим значе­нием переменного синусоидального тока. По аналогии введём понятия дейст­вующих значений э.д.с. и напряжения:

;	(3.15)
.	(3.16)

Электроизмерительные приборы показывают действующие значения изме­ряемых величин (тока, напряжения).

Пример 3.5

В цепи протекает электрический ток i = 14,1 sin (t – 37) А.

Определить показание амперметра, включённого в цепь.

Решение.

Амперметр показывает действующее значение тока, которое определяем по (3.14), подставив амплитуду тока:

.