3. Вопросы к домашнему заданию
1. Что такое электропроводность, дрейфовая скорость, подвижность и длина свободного пробега носителей заряда? Как они связаны между собой?
2. Чем обусловлен электрический ток в металлах, сплавах и полупроводниках?
3. Приведите выражение для удельной проводимости чистых металлов.
4. Нарисуйте и проанализируйте типичную температурную зависимость удельного сопротивления металлов.
5. Объясните зависимость удельного сопротивления сплавов от состава и температуры.
6. В чем заключаются правила Маттиссена и Курнакова – Нордгейма?
7. Как зависят концентрация и подвижность носителей заряда для собственных и примесных полупроводников?
8. Приведите и объясните температурную зависимость удельной проводимости полупроводника.
9, Какой фактор является определяющим для температурной зависимости удельной проводимости полупроводников, а какой – для металлов?
4. Лабораторные задания и методические указания по их выполнению
4.1. Задание № 1
Ознакомиться с устройством экспериментальной установки и занести ее схему в отчет. Измерить сопротивление меди, константана и селена при комнатной температуре, рассчитать их удельные сопротивления.
Схема установки представлена на рис. 4. Исследуемые образцы размещены в термошкафу. Измерение сопротивления металлических образцов осуществляется с помощью потенциометра УПИП-60М, для измерения сопротивления полупроводника используется вольтметр В7-16А. Удельное сопротивление определяется из выражения
,
(18)
где R – сопротивление образца; S – площадь поперечного сечения; l – длина.
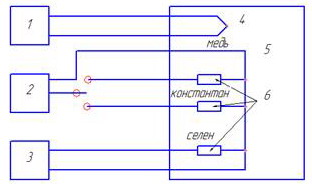
Рис. 4. Схема экспериментальной установки для изучения
температурных зависимостей проводимости металлов,
сплавов и полупроводников: 1 – вольтметр В7-21;
2 – потенциометр УПИП-60М; 3 – вольтметр В7-16А;
4 – термопара хромель-алюмель; 5 – термошкаф;
6 ‑ Образцы
В работе используются металлические проволочные образцы диаметром 0,1 мм (S = 7,85·10–3 мм2) и длиной: медь – 0,96 м, константан – 0,6 м.
Для определения удельного сопротивления полупроводника обычно используется четырехзондовый метод, позволяющий избежать паразитного влияния контактной разности потенциалов, возникающей на границе металла с полупроводником. Контактная разность потенциалов приводит к тому, что сопротивление переходных слоев может в несколько раз превышать сопротивление исследуемого полупроводника. В данной установке используется надежный омический контакт, имеющий маленькое сопротивление. Это позволяет использовать для измерения более простую стандартную методику.
Пленка селена с акцепторной примесью, нанесенная на диэлектрическую подложку, имеет следующие размеры: длина l = 10 мм, ширина d = 100 мм, толщина h = 60 мкм (S = 6 мм2).
Сравните рассчитанные удельные сопротивления исследованных образцов с табличными данными: ρмедь = = 1,75·10–8 Ом·м; ρконст. = (4,4 – 5,2)·10–7 Ом·м; ρселен ≈ ≈ 8·103 Ом·м.
4.2. Задание № 2
Снять температурные зависимости удельных сопротивлений меди, константана и селена. Построить графики зависимостей ρ = f(Т) для меди и константана и γ = f(1/Т) для селена. Из этих графиков определить ширину запрещенной зоны полупроводника и температурные коэффициенты удельного сопротивления αρ для металлов.
Для выполнения задания необходимо подключить термошкаф к сети и провести измерения сопротивлений всех испытуемых образцов через 10 °С до 80 °С. Температура измеряется хромель-алюмелевой термопарой с помощью вольтметра В7-21. Перевод показаний вольтметра в градусы Цельсия приведен в табл. 1.
Таблица 1
Показания вольтметра, мВ |
0,00 |
0,40 |
0,80 |
1,20 |
1,61 |
2,02 |
2,43 |
Температура, °С |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
Результаты измерений необходимо занести в табл. 2.
Таблица 2
t, °С |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
Т, К |
|
|
|
|
|
|
|
1/Т, К–1 |
|
|
|
|
|
|
|
Rмедь, Ом |
|
|
|
|
|
|
|
ρмедь, Ом·м |
|
|
|
|
|
|
|
Rконст., Ом |
|
|
|
|
|
|
|
ρконст., Ом·м |
|
|
|
|
|
|
|
Rселен, Ом |
|
|
|
|
|
|
|
ρселен, Ом·м |
|
|
|
|
|
|
|
γселен, Ом–1·м–1 |
|
|
|
|
|
|
|
lnγселен |
|
|
|
|
|
|
|
Температурный коэффициент удельного сопротивления αρ определяется из формулы (7). Сравнить полученные значения с αρ большинства металлов, который при комнатной температуре составляет 0,004 К–1.
Ширина запрещенной зоны и энергия активации примесей находятся из температурной зависимости логарифма удельной проводимости селена. Как видно из рис. 3, зависимость lnγ = f(1/Т) полупроводника изображается прямыми линиями, тангенсы углов наклона которых равны ΔЭпр/2k и ΔЭ/2k. Поэтому для выполнения задания необходимо по экспериментальным данным построить график в координатах lnγ – 1/Т, провести через экспериментальные точки на этом графике усредненную прямую, по тангенсу угла наклона определить ширину запрещенной зоны.
Перевести полученные значения в электрон-вольты (1 Эв = 1,6·10–19 Дж) и сравнить с величиной ΔЭ = 1,7 Эв для чистого селена, сделать соответствующие выводы.