Глава 3. Электрическая дуга и ее гашение

3.1. Физические параметры дуговой плазмы

В этом параграфе приведены задачи по некоторым исходным физическим параметрам и связи между ними (например, определение длины свободного пробега электрона в дуговой плазме и ее зависимости от температуры и давления газа, энергии электрона, степени ионизации газа с помощью уравнения Саха, решение вопроса рекомбинации ионизированных частиц и передачи энергии от дугового столба к окружающей газовой среде). Решение таких задач дает возможность ознакомиться с некоторыми физическими закономерностями и числовыми значениями наиболее употребительных величин в теории газового разряда высокого давления. При этом используются следующие формулы и соотношения.

Длина (см) свободного пробега электрона.

где N_Т - число молекул в 1 см³ газа при температуре Т; d - диаметр молекулы газа, см.

84

Средняя энергия электронов (эВ), ускоряемых в электрическом поле напряженностью Ε (В/см),

Мощность, отводимая в воздухе с 1 см длины дуги путем теплопроводности,

где Т - температура дуги, К.

Мощность, отводимая от 1 см длины дуги путем поперечной конвекции,

где T - температура дуги, К; T₀ - температура окружающей среды, К; v - скорость поперечного потока воздуха, м/с; d - диаметр столба дуги, см, определяемый по формуле

где I - ток в дуге, А.

Формула Саха

где p - давление газа, Па; x - относительная ионизация в долях единицы, V_и - энергия ионизации, эВ; Т - температура, К.

Начальная скорость спада плотности ионов в ионизированном газе за счет рекомбинации

где α - коэффициент рекомбинации.

3.1.1. Определить среднюю длину пробега электрона в азоте при атмосферном давлении и температуре газа T=5000 К.

Решение. Длина свободного пробега электрона определится из (3.1), где d=3,146·10^-8 см - диаметр молекулы азота (см. табл. П.22). Для нахождения λ_э необходимо знать Ν_т. Известно, что число молекул любого газа в 1 см³ при атмосферном давлении и 0°С N₀=2,7·10¹⁹ см^-3.

Определим Ν_т, считая, что число частичек газа в 1 см³ (плотность газа) при температуре Т находится в обратном отношении абсолютных температур, т.е. Ν_т=Ν₀Τ₀/Т =2,7·10¹⁹·273/5000= 14,74·10¹⁷ см^-3, тогда средняя длина свободного пробега электрона из (3.1)

Ответ: λ_э=0,88·10^-3 см.

3.1.2. Определить среднюю длину свободного пробега электрона в атмосфере кислорода при давлении p=2·10⁵ Па и температуре T=7000 К.

3.1.3. Определить среднюю длину свободного пробега электрона в атмосфере водорода при давлении р = 3·10⁵ Па, температуре Т = 8000 К.

3.1.4. Определить среднюю энергию электрона в азоте, приобретаемую им в электрическом поле напряженностью Е = 50 В/см при температуре газа Т = 10000 К и давлении газа р=9,8·10⁴Па.

85

Решение. Если заряд электрона принять за единицу, то средняя энергия электронов, ускоряемых в электрическом поле напряженностью E, определится из (3.2)

Здесь λ_э = 4/(πN_тd²) =4/[3,14·7,37·10¹⁷(3,146)²·10^-16] = 1,6·10^-3 см - средняя длина свободного пробега электрона в азоте, Ν_т = Ν₀Τ₀/Τ=2,7·10¹⁹·273/10000 = 7,37·10¹⁷; d=3,146·10^-8 (см. табл. П.22).

Ответ: A_э=80·10^-3 эВ.

3.1.5. Определить среднюю энергию электрона в атмосфере азота, приобретенную им в электрическом поле напряженностью E=100 В/см при температуре газа T=10000 К и давлении р = 3·10⁵Па.

3.1.6. Определить среднюю энергию электрона в атмосфере водорода, приобретенную им в электрическом поле напряженностью E=100 В/см при температуре газа T=18000 К и давлении р = 5·10⁵Па.

3.1.7. Определить мощность, отводимую поперечным потоком воздуха, скорость которого v = 3 м/с. Температура газа в дуговом столбе Т=5000 К, температура окружающей среды T₀=300 К. Ток в дуге I=50 А. Полученный результат сопоставить с мощностью, отводимой за счет теплопроводности в воздухе.

Решение. Мощность, отводимая в воздухе с 1 см длины дуги путем теплопроводности, в соответствии с (3.3)

Диаметр дугового столба при относительной скорости движения его в среде определим по формуле Брона

Мощность, отводимая за счет конвекции [см. (3.4)],

Ответ: Р_к = 2090 Вт/см.

3.1.8. Оценить мощность, отводимую от дугового столба длиной в 1 см путем излучения, если ток в дуге I=5000 А, напряженность поля E=80 В/см. Электроды выполнены из меди.

3.1.9. Определить мощность, отводимую от дугового столба длиной в 1 см за счет теплопроводности. Температура T=7000 К.

3.1.10. Определить мощность, отводимую от дугового столба длиной в 1 см путем конвекции газа (азота). Скорость движения дуги v=25 м/с, температура газа в дуговом столбе T=8000 К, температура окружающей среды Т = 500 К.

3.1.11. Оценить мощность, отводимую с 1 см длины дуги путем конвекции, при условии, что температура столба дуги Т= 3000 К, температура окружающей среды Т=320 К, диаметр - дуги d=l,5 см, скорость проникновения (средняя) холодного потока газа в дуговой столб v = 50 м/с.

86

3.1.12. Оценить и сравнить долю общей рассеиваемой дуговым столбом мощности по существующим эмпирическим формулам. Ток дуги I=5000 А, падение напряжения в столбе U = 200 В/см.

3.1.13. Вычислить и построить кривую мощности дуги длиной l=5 см за полупериод переменного тока при условии, что ток в дуге изменяется по закону i =450 sin ωt, а напряжение на дуге

3.1.14. Какая часть от общего числа частичек газа находится в ионизированном состоянии при условии, что энергия ионизации атома газа V_и=15 эВ, температура газа T=12000 К, давление p=4·10⁵ Па?

Решение. Связь между относительной ионизацией газа, его температурой Т, энергией ионизации V_и и давлением p можно выразить с помощью уравнения Саха (3.6). Обычно полагают, что x≪1, и поэтому

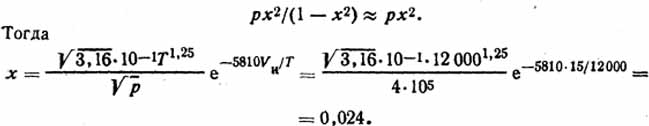
Ответ: х=0,024.

3.1.15. Определить начальную скорость спада плотности ионов в ионизированном газе за счет рекомбинации, а также плотность ионов спустя 10 мкс с начала процесса, если коэффициент рекомбинации α = 10^-9 и начальная плотность ионов в остаточном столбе n₀=10¹⁵.

Решение. Начальную скорость спада плотности ионов определим по формуле (3.7)

Решение уравнения (3.7) дает зависимость n=n(t), т.е. плотность ионов спустя время t. Для t=10^-5 с будем иметь n=n₀/(1+n₀αt) = 10¹⁵/(1 + 10¹⁵·10^-9·10^-5)=0,91·10¹⁴ пар ионов.

Ответ: dn/di= -10^-21 с^-1; n=0,91·10¹⁴ пар ионов.

3.1.16. Определить начальную скорость спада плотности ионов в ионизированном газе дугового столба, если коэффициент рекомбинации газа α=10^-9, начальная плотность ионов n₀=10¹⁵.

3.1.17. Построить для частного случая зависимость спада во времени плотности ионов в дуговом столбе за счет рекомбинации ионов. Коэффициент рекомбинации газа α=2·10^-9, начальная плотность ионов n₀ = 10¹⁵.

87