6. Общ ур линий второго порядка (центральные линии).

Приведение к конанич виду в два этапа: на первом - поворос с.к. таким образом что бы ур-ие не содержало xy (т.е. b^|=0). На втором – параллельный перенос с.к.

1этап) Если ур-ие не содержит xy то первый этам можно пропустить. Если b не равн нулю: ((далее тупо подставить в ур крив)) …

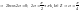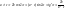Пусть ; 1 случай) если а=с ; 2 случ) если ; После первого этапа ур кривой бедет иметь вид:

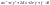
Второй этап: ((центр кривы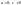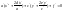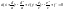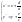е)) ; ; ; ; , где 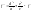Если ;

1) если - эллипс

2) если - мнимый эллипс

3) если 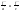разных знаков - гипербола

4) если 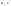одного знака – пара мнимых пересек прямых ( )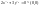

5) если разных знаков – пересек прямые ( )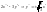

Теорема: ((в след билете))

Общ ур линий второго порядка (НЕцентральные линии).

Приведение к конанич виду в два этапа: на первом - поворос с.к. таким образом что бы ур-ие не содержало xy (т.е. b^|=0). На втором – параллельный перенос с.к.

1этап) Если ур-ие не содержит xy то первый этап можно пропустить. Если b не равн нулю: ((далее тупо подставить в ур крив)) …

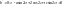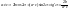Пусть ; 1 случай) если а=с ; 2 случ) если ; После первого этапа ур кривой бедет иметь вид:

Второй этап: ((нецентр кривые)) ; либо либо 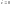; пусть ; ;

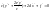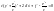
1) если 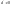: 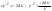- порабола

если : ; (пар перенос) , где

2) если - пара парал прямых

3) если 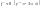- пара мнимых парал прямых

4) если - пара совп прямых

7. Классификация кривых 2-го порядка.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов   отличен от нуля.

Классификация кривых второго порядка:

1)Невырожденные кривые

Кривая второго порядка называется невырожденной, если   Могут возникать следующие варианты:

• Невырожденная кривая второго порядка называется центральной, если 

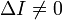
эллипс - при условии D > 0 и ΔI < 0;

частный случай эллипса — окружность — при условии

 I² = 4D или a₁₁ = a₂₂,a₁₂ = 0;

мнимый эллипс (ни одной вещественной точки) — при условии ΔI > 0;

гипербола — при условии D < 0;

Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0

парабола — при условии D = 0.

2)Вырожденные кривые

Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:

вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;

пара вещественных пересекающихся прямых (вырожденная гипербола) - при условии D<0;

вырожденная парабола — при условии D = 0:

пара вещественных параллельных прямых — при условии B < 0;

одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;

пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.