10.Смешанное произведение 3 векторов. Ориентированный V паралелепида

. Опр: Смешанное произ 3 векторов равно числу равному скалярному произведению векторного произведения 2 первых векторов на 3ий. Опр: Ориентированным объёмом паралел-да построенного на векторах наз объём паралел-да, взятым со знаком + если эти векторы обр правую тройку и – если тройка левая.

Свойства смешанного произв.

1) смешанное произведение 3 векторов равно ориентированному объёму паралел-да постр на этих векторах. Док-во:

1 случай) - правая тройка,

2 случай) -левая тройка.

2) 3) Смеш произв не меняется при циклических перестановках векторов 4) Если сомножителм поменять местами, произвед поменяет знак 5) Векторы компланарны между собой тогда и только тогда когда

11. Вект и смеш произв вект в коорд

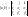Вект: Теорема: Д-во: Смеш: теорема:

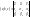
д-во: ;

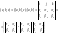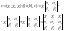
2.Уравнение кривых и поверхностей.

1. Общ дек систа коорд. Коорд тчк. Выч расст межд тчк.

Д.с.к определяется заданием точки и базиса 3д пространства (т. О {e₁,e₂,e₃}) Прямые проход через т О назыв осями коор-т (х-абцис, у-ординат, z-аппликат) Плоскости проход через оси – назаыв коорд плоск-ми.

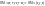- радиус вектор т М; в базисе координаты т М назыв коорд-ми ее рад вект-а. Если С лежит на АВ, то Д-во: (так же y,z).

Прямоуг д.с.к – ее базис ортонормированный. ({O,i₁,j₂,k₃} – прав тройка).

2.Расстояние между двумя точками

Расст межд тчкми: если в прям.д.с.к

3. Полярная сист коорд на пл-сти.

т О – полюс, луч L – полярная ось. R – полярн радиус, r≥0, r=0=O, φ – полярн угол. Если угол отсчит-ся против час стрелки, то его значение счит-ся положительн, если против – отриц. Полярн угол опред-ся с точностью до слагаемого 2π (-π<φ≤ π или 0<φ≤ 2π). Связь с прямоуг.д.с.к:

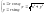
4. Уравн линий и поверхн

Линия на плоск – это множество точек, координаты которых удовл F(x,y)=0, данное ур-е должно иметь решение и не должно быть тождеством, в этом случае говорят, что кривая задана не явно. Если кривая задается множ-ом тчк y=f(x)– явно. (x+1024y-1100=0 - прямая). Если в неявном ур-ии кривой F(x,y)=0, F(x,y) – многочлен относ x,y то такая кривая – алгебраическая. Степень данного мн-на порядок кривой. Если F(x,y) нельзя представить в виде мн-на относ x,y то кривая назыв трансцендентной. (Ax+By+C=0 – алг, y=cosx - трансц). Параметрич ур-ями кривой наз ур-ия вида , где t – параметр, котор приним знач от а до b (a≤t≤b) F(x,y)=0 => F(x(t),y(t))=0 (y-kx-b=0

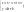
Поверхностью в 3д пространсте назыв множ-во тчк корд-ты кот-ых удовл: F(x,y,z)=0 если пов-сть задается z=z(x,y) то говорят что пов-сть задана явно (Ур-ие F(x,y,z)=0 имеет реш и не явл тожд) (x,y,z) – прям.д.с.к. (Ax+By+Cz+D=0) (про мн-ны, алг и трансц тоже самое) парам-ское Ур-ие: , u,v – парам. Кривая может быть задана как пересечение двух поверхностей или парам ур. (x=x(t) и тд)