
- •1.Вектор.Свойства.
- •2.Проекция на ось.
- •3.Базис системы векторов
- •5.Базис множества всех векторов в трехмерном пространстве.
- •6.Скалярное произведение векторов
- •7.Вычисление скалярного произведения векторов через координаты
- •9.Ориентация. Векторное произведение.
- •10.Смешанное произведение 3 векторов. Ориентированный V паралелепида
- •11. Вект и смеш произв вект в коорд
- •2.Уравнение кривых и поверхностей.
- •1. Общ дек систа коорд. Коорд тчк. Выч расст межд тчк.
- •2.Расстояние между двумя точками
- •3. Полярная сист коорд на пл-сти.
- •4. Уравн линий и поверхн
- •3.Прямые и плоскости
- •1.Прямая на плоскости.Общее Ур-ние.Нормальный вектор.Направя cosы вектора.Урние прямоы проход через точку.Параметрические урния. Ур-ние прямой проход через 2 задан точки. В отрезках на осях.
- •2.Взаимн расп прямых на плоскости.Угол между 2 прямыми.
- •5. Расст от тчк до пл. Норм ур плоскости.
- •6. Взаимн расп двух пл-ей в простр. Угол между пл.
- •7. Прямая в простр. Общ ур пр. Ур пр, проход через 2 заде тчки.Параметрич., конанич. Уравнения прямой.
- •2.Гипербола. Вывод канонического уравнения. Свойства. Асимптоты
- •3. Парабола. Вывод канонического уравнения. Свойства.
- •4.Родство эллипса, гиперболы и параболы.
- •5.Преобразование прям д с к.
- •6. Общ ур линий второго порядка (центральные линии).
- •7. Классификация кривых 2-го порядка.
- •Классификация кривых второго порядка:
- •1)Невырожденные кривые
- •2)Вырожденные кривые
- •8 . Эллипсоид. Канон ур-ие. Сечения. Эллипсоиды вращения.
- •9. Гипербалоиды
- •10. Конус.
- •11. Параболоиды
- •14. Поверхности вращения.
- •15.Поворт трехмерного пространства
- •16. Точечные преобразования. Движения. Поворот, параллельный перенос, симметия, общее преобразование.
1.Вектор.Свойства.
Вектор- направленный отрезок, нулевой вектор-точка. Длина вектора- длина отрезка вектора или расстояние от начала до конца. Два вектора равные если: лежат на парал. прямых или на одной. их длины равны, напр в одну сторону. Векторы, которые лежат на парал прямых или на одной- коллинеарные, 2 коллин. вектора напр в одну сторону- соноправл., в разнае стороны- противополнапр. векторы лежащ на парал прямых – компланарные.
Операции: 1.Сложение:правило треуг, правило парал-рама.
2.Умножение
вектора на число:
Произведение вектора А на число α наз
В: 1) В колинеарен А, 2) соноправлен, есль
α >0 против. есль α <0 3) |В|=| α |*|А|
Теорема:
пусть А 0,
В коллин А, тогда
0,
В коллин А, тогда
 α: В= α А. Док-во:
В= α *|А|=> |В|=| α |*|А|=> | α |=|В|/|А|=>
α: В= α А. Док-во:
В= α *|А|=> |В|=| α |*|А|=> | α |=|В|/|А|=>
 Единственность: Пусть сущ α1
и α2 =>
В=| α1 |*|А|=|
α2 |*|А|
=> | α1
|*|А|=| α2
|*|А| , А
0,
| α1 |=|
α2 |
=> α1 =
Единственность: Пусть сущ α1
и α2 =>
В=| α1 |*|А|=|
α2 |*|А|
=> | α1
|*|А|=| α2
|*|А| , А
0,
| α1 |=|
α2 |
=> α1 =
 α2;
α1 =
α2
или α1 =
- α2
(не может).
α2;
α1 =
α2
или α1 =
- α2
(не может).
Свойства операций:
1)А+В=В+А, 2)(А+В)+С=А+(В+С), 3)А+0=А, 4) Для А В:
А+В=0. Опр:
Разностью А-В=А+(-В). 5) α
(А+В)= α
А+ α
В 6) (α +β)А=
α А+ β А. Док-во:
1) α и β одного знака: Длина:
В:
А+В=0. Опр:
Разностью А-В=А+(-В). 5) α
(А+В)= α
А+ α
В 6) (α +β)А=
α А+ β А. Док-во:
1) α и β одного знака: Длина: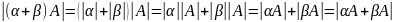 Направл:
Направл:
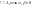 =>
=>
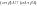 ;
;
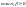 =>
=> ,
,

 }=>
}=>

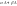 .
2)α и
.
2)α и разного
знака: а) | α |=| β | α = - β => (α + β)А=0, α А+
β А=0 => 0=0 б) | α |>| β|
разного
знака: а) | α |=| β | α = - β => (α + β)А=0, α А+
β А=0 => 0=0 б) | α |>| β|
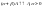 ,
, ,
, ,
,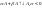 }=>
}=>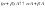 .Длина:
.Длина:
 .
7) α (βА)= (αβ)А 8)1*А=А
.
7) α (βА)= (αβ)А 8)1*А=А
2.Проекция на ось.
Опр: Осью наз прямую на которой задано направл. Оно задается произвольным не 0вым вектором. Опр: Рассм множество векторов плоскости.
![]()
-проекция вектора на ось(рис)
Рассм произв ось.
Пусть l
прямая пересек ось в произв точке. Еще
есть точка М(не лежащая на оси). Проводим
через нее прямую || l.
Получаем
 -проекцию
точки на ось вектора А || l
-проекцию
точки на ось вектора А || l
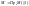 .
Опр: Рассм множество всех векторов 3-х
метром пространстве. Берется ось, через
нее проводится плоскость Пи. Берется
М, через нее проводится еще одна плоскость
|| Пи
.
Опр: Рассм множество всех векторов 3-х
метром пространстве. Берется ось, через
нее проводится плоскость Пи. Берется
М, через нее проводится еще одна плоскость
|| Пи
 .
Алгебраич значением проекции вектора
на ось наз число которое опр след
образом:
.
Алгебраич значением проекции вектора
на ось наз число которое опр след
образом:

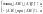 Свойства
алгебр значений:
Свойства
алгебр значений:
1)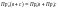 2)
2)
 .
Опр: Под углом между векторами будем
принимать угол между векторами равных
данным и имеющими общее начало и
абсолютной величине не больше 180. По
часовой угол с минусом, против +. Опр:
Рассм проекциб вектора на ось || l
или || плоскости Пи., если эта прямая или
плоскость перпендик оси, то она
ортогональна. Теорема:
Алгебр значение ортогональной проекции
АВ на ось вектора а
.
Опр: Под углом между векторами будем
принимать угол между векторами равных
данным и имеющими общее начало и
абсолютной величине не больше 180. По
часовой угол с минусом, против +. Опр:
Рассм проекциб вектора на ось || l
или || плоскости Пи., если эта прямая или
плоскость перпендик оси, то она
ортогональна. Теорема:
Алгебр значение ортогональной проекции
АВ на ось вектора а
 Док-во:
Док-во:
1)
 ,
проводим ||AB
из точки С (лежащей на оси), получается
CD
,
проводим ||AB
из точки С (лежащей на оси), получается
CD
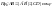 => т.к. длины АВ и CD
равны =>
=> т.к. длины АВ и CD
равны =>
2)
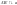 ,
,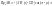
 .
.
3.Базис системы векторов
Опр:
Рассм некоторую систему векторов:
 вектор равный:
вектор равный:
 наз
линейной комбинацией. Если комбинация
системы =0, тока если все
наз
линейной комбинацией. Если комбинация
системы =0, тока если все
 ,
система векторов- линейно независима,
в обратном- зависима. Опр:
Наз базисом системы векторов, такую её
подсистему, что выполняется: 1) подсистема
линейнонезависима, 2)произ вектор можно
представить в виде линейной комбинации
данной подсистемы. Опр:
Число векторов в базисе- размерность
системы. Теорема:
Пусть
,
система векторов- линейно независима,
в обратном- зависима. Опр:
Наз базисом системы векторов, такую её
подсистему, что выполняется: 1) подсистема
линейнонезависима, 2)произ вектор можно
представить в виде линейной комбинации
данной подсистемы. Опр:
Число векторов в базисе- размерность
системы. Теорема:
Пусть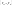 базис
некоторой подсистемы, тогда любой
вектор системы единственным образом
может быть представлен в виде:
базис
некоторой подсистемы, тогда любой
вектор системы единственным образом
может быть представлен в виде:
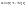 Док-во:
(от обратного,единств)
Пусть
Док-во:
(от обратного,единств)
Пусть
 =>
=> ,
т.к.
,
т.к.
 -базис
и лин независ система>
-базис
и лин независ система>
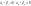 =>
=>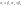 .
Опр:
Представление
.
Опр:
Представление
 наз
разложением вектора по базису, а
наз
разложением вектора по базису, а
 -
координаты вектора а, в базисе
-
координаты вектора а, в базисе
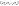 Теорема:
Пусть
базис
некоторой системы векторов. При сложении
2 произвольных векторов системы, их
координаты в базисе складываются, при
умножении вектора на число, все координаты
вектора умножаются на число. Док-во:
Рассмотрим
2 вектора
Теорема:
Пусть
базис
некоторой системы векторов. При сложении
2 произвольных векторов системы, их
координаты в базисе складываются, при
умножении вектора на число, все координаты
вектора умножаются на число. Док-во:
Рассмотрим
2 вектора
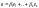

 -
координаты
-
координаты
 в базисе
в базисе
 .
Умножение:
.
Умножение:


 -
координ
-
координ
 в
базисе
в
базисе
4.Базис множества всех векторов на прямой и плоскости.
Теорема1:
Произвольный не 0ой вектор обр базис
множества всех векторов прямой. Док-во:
Рассмотрим
любой
 1)
1)
 -лин
независ система векторов,т.к.
-лин
независ система векторов,т.к.
 =>
=> =>
=>
 =>
=> .
2) Любой произвольный вектор принадлеж
прямой.
.
2) Любой произвольный вектор принадлеж
прямой.
 коллинеарен
коллинеарен

 :
:
 координата вектора в базисе
=>
множество всех векторов на прямой обр
базис величиной 1. Теорема2:
координата вектора в базисе
=>
множество всех векторов на прямой обр
базис величиной 1. Теорема2:
2 произв
неколинеарн
вектора обр базис множества всех
векторов плоскости. Док-во:
Пусть
 произ
неколин векторы. 1)
произ
неколин векторы. 1)
 лин
независ система векторов, т.к. оба они
не равно нулю, т.к. о коллинеарен всем.
Подставл в лин комбинацию:
лин
независ система векторов, т.к. оба они
не равно нулю, т.к. о коллинеарен всем.
Подставл в лин комбинацию:
 ,
от обратного. Пусть
,
от обратного. Пусть

 противоречие.
=>
лин независ система.
противоречие.
=>
лин независ система.
2)

 .
.

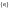 базис
на АВ.
базис
на АВ.

 базис
на АС=>
базис
на АС=>
 координаты
вектора
в
базисе
.
координаты
вектора
в
базисе
.
