
- •Предисловие.
- •Введение.
- •Предметы и задачи курса.
- •Классификация основных процессов химической технологии.
- •Гипотеза сплошности среды.
- •1.4. Режимы движения жидких сред.
- •1.5. Силы и напряжения, действующие в жидких средах.
- •Сила поверхностного натяжения.
- •Массовые силы.
- •2. Теоретические основы пхт.
- •2.1. Основы теории переноса.
- •2.1.1. Основные понятия.
- •2.1.2 Механизмы переноса субстанций.
- •Конвективный механизм.
- •Турбулентный механизм.
- •2.1.3. Условие проявления и направления процессов переноса.
- •2.1.4.Уравнения переноса субстанций.
- •2.1.4.1. Перенос массы. Молекулярный механизм переноса массы.
- •Конвективный механизм переноса массы.
- •Если учесть, что молекулярная диффузия сохраняется и при турбулентной диффузии можно записать:
- •Перенос энергии.
- •Теплота- форма передачи энергии на микроуровне.
- •Молекулярным механизмом перенос энергии осуществляется в форме тепла. Поток тепла за счет молекулярного механизма в условиях механического и концентрационного равновесия может быть представлен в виде:
- •Конвективный механизм переноса энергии.
- •Турбулентный механизм переноса энергии.
- •Перенос импульса.
- •Молекулярный перенос импульса.
- •Законы сохранения субстанции.
- •2.1.5.1 Закон сохранения массы.
- •Интегральная форма (материальный баланс).
- •Изменение массового расхода в объеме dV только за счет изменения плотности:
- •Закон сохранения энергии.
- •Интегральная форма закона сохранения энергии(первый закон термодинамики).
- •Работа может совершаться движущейся средой по преодолению внешнего давления и трения:
- •– Уравнение Фурье-Кирхгофа.
- •Закон сохранения импульса.
- •Локальная форма закона сохранения импульса.
- •Здесь: - суммарный поток импульса,
- •Исчерпывающее описание процессов переноса.
- •Условия однозначности.
- •2.1.5.2 Поля скорости, давления, температуры и концентраций. Пограничные слои.
- •Аналогия процессов переноса.
- •Межфазный перенос субстанции.
- •Уравнения массо-, тепло-, импульсоотдачи. Локальная форма уравнений.
- •Уравнения массо-, тепло- и импульсопередачи.
- •Локальная фаза уравнений.
- •Предположим i1 i2 , тогда:
- •Здесь Кid – коэффициент массопередачи, (яi1 - яi2) – движущая сила массопередачи. Уравнение (2.79) носит название уравнения массопередачи.
- •2.2.2.2.Интегральная форма уравнений.
Аналогия процессов переноса.
Аналогия уравнений переноса соответствующих субстанций и законов сохранения обуславливается идентичностью механизмов переноса субстанций. Полная аналогия, т.е. совпадение полей Ci и T, возможна для переноса массы и тепла в двухкомпонентных системах при а = D12 и aт = Dт. В случае многокомпонентных систем аналогия нарушает наличие матрицы коэффициентов многокомпонентной диффузии.
В общем случае отсутствует аналогия в процессах переноса импульса с переносом массы и энергии вследствие векторной природы первой и скалярной двух последних, а также наличие в уравнениях Навье-Стокса двух дополнительных членов, учитывающих влияние на перенос импульса массовых сил и сил давления. Однако, гидродинамическая аналогия возможна в частных случаях, как, например, при рассмотрении пограничного слоя на плоской горизонтальной пластине.
Удобства применения аналогии процессов переноса – возможность использования результатов исследования одних процессов для описания других. В этом случае необходимо соблюдение аналогии не только дифференциальных уравнений, но и условия однозначности к ним.
Межфазный перенос субстанции.
Проведение процессов химической технологи сопровождается переносом субстанций из ядра одной фазы через границу раздела фаз в ядро другой фазы. В зависимости от вида переносимой субстанции можно выделить массо-, тепло-, импульсопередачу. В процессе межфазного переноса субстанции можно выделить три стадии:
перенос субстанции от ядра первой фазы к границе раздела фаз;
перенос через границу раздела фаз;
перенос от границы раздела фаз к ядру второй фазы.
Перенос от границы раздела фаз к ядру фазы или от ядра к границе в зависимости от вида субстанции называют массо-, тепло-, импульсоотдачей.
Уравнения массо-, тепло-, импульсоотдачи. Локальная форма уравнений.
Рассмотрим элементарный участок межфазной поверхности dF, совпадающей с плоскостью XOY. Поток субстанций направлен вдоль оси Z, движение фазы по оси X.
Z
Wx

![]()
![]()
![]()


 X
X

Рис.2.5
Рассмотрим поток субстанций за счет молекулярного и турбулентного механизмов переноса:
jdгiz – диффузионный поток массы,
qтгz – поток тепла за счет теплопроводности,
вгzx – вязкий поток импульса (тензор вязких напряжений).
Как правило, конвективный перенос субстанции через границу раздела фаз отсутствует.
Проекция теплового потока за счет теплопроводности на ось Z по закону Фурье:
qтгz = -( + т)* dT/dz z=0 (2.64)
использование этого закона затруднительно, так как неизвестен закон распределения температур в тепловом пограничном слое т. В пределах т температура меняется от Тг (температура поверхности раздела фаз) до Тя (температура на внешней границе теплового пограничного слоя, равной температуре ядра). В ядре фазы температура не меняется. По закону Ньютона тепловой поток qтгz может быть записан:
qтгz = (Тг - Тя) (2.65)
Здесь - коэффициент теплоотдачи. Коэффициент теплоотдачи зависит от многих факторов: режима движения и физических свойств среды, геометрических параметров каналов и т.д.
Аналогичным образом могут быть получены уравнения массо- и импульсоотдачи:
Jdгiz= i (Cгi - Cяi) = i(гi - гi) (2.66)
вгzx = j(Wгx - Wгx) (2.67)
Здесь i, j – коэффициенты массо-, и импульсоотдачи.
Разница значений субстанций у границы раздела фаз и в ядре фазы носит название движущей силы процесса отдачи субстанции. Коэффициент массо-, тепло-, импульсоотдачи определяется:
i =
 м/с
(2.68)
м/с
(2.68)
= Вт/м2с
2.69)
Вт/м2с
2.69)
j =
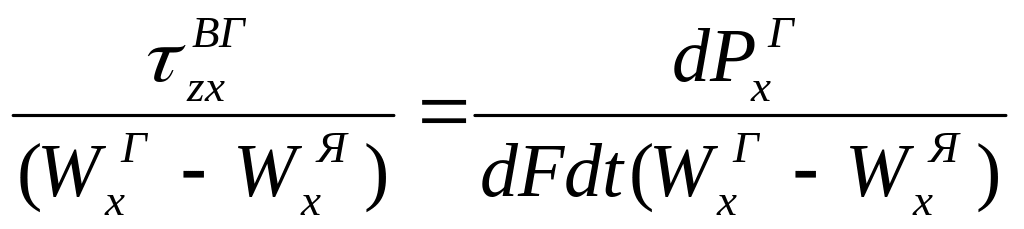 кг/м2с
(2.70)
кг/м2с
(2.70)
Следовательно, коэффициенты массо-, тепло-, импульсоотдачи являются кинетическими характеристиками этих процессов и отражают, соответственно, количество вещества (компонента), тепла и импульса, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности и приходящиеся на единицу движущейся силы.
Коэффициенты массотдачи рассмотрены для бинарных сред.
При ламинарном течении жидкой среды вместо значения переменной в ядре потока в уравнениях (2.65) – (2.70) используют осредненное по поперечному сечению значение. Для ламинарного режима течения модель пограничного слоя не работает.
