– Уравнение Фурье-Кирхгофа.

При теплопереносе в неподвижной среде (W = 0) получим уравнение нестационарной теплопроводности Фурье:

= a²T (2.54)

Для случая стационарного переноса тепла получено:

²Т = 0 (2.55)

Решение дифференциальных уравнений, полученных на основе закона сохранения совместно с условиями однозначности, позволяет получить поля температуры и поток тепла в аппарате.

2. Закон сохранения импульса.

Суммарный импульс изолированной системы есть величина постоянная =0, =0. Если же система находится под воздействием внешних сил, то производная от импульса системы по времени равна результирующей силе, действующей на систему.

Интегральная форма закона сохранения импульса.

Изменение импульса в фиксированном объеме V вызывается разностью прихода и отвода импульса, а так же источником импульса. Как известно, импульс является величиной векторной:

(2.56)

Здесь _вх , _вых – приход и отвод импульса, из объема V за время t, r- количество импульса образующегося в единице объема за единицу времени (источник импульса).

Локальная форма закона сохранения импульса.

Аналогично законам сохранения массы и энергии можно получить локальную (для точки) форму закона сохранения импульса.

С корость результирующая сила силы

Накопления = скорость поступления + давления + массовые

импульса импульса

Отличие будет заключаться лишь в векторной природе переносимой субстанции – импульса единичного объема W.

(2.57)

Здесь: - суммарный поток импульса,

– ускорение.

Если массовая сила есть сила тяжести, то = g.

Р асчленив тензор потока импульса  на конвективную часть и тензор вязких напряжений _в по (2.27) , можно представить общий вид уравнения движения с локализованием субстанциональной производной:

(2.58)

Здесь:

Допустив  = const (молекулярная вязкость) для ламинарного движения получим: уравнение Навье-Стокса:

: (2.59)

Разделив уравнение (2.59) на  получим привычный вид уравнения Навье-Стокса:

: (2.60)

Развернутый вид уравнения (2.60) для оси X в декартовой системе координат имеет следующий вид 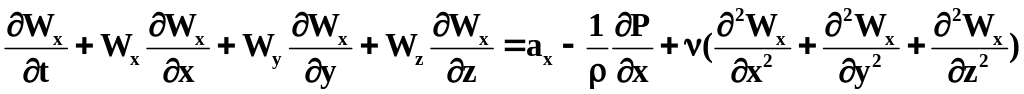(2.61)

Остальные уравнения по осям y,z могут быть получены заменой индексов по кругу xyzx.

Рассмотрим частные случаи уравнения Навье-Стокса: Если среда идеальная, то  = 0 и получим:

(2.62)

Уравнение Эйлера.

Если среда находится в равновесии, то W = 0 и получим:

(2.63) - Уравнение равновесия Эйлера.