Уравнение сплошности (неразрывности движения), его физический смысл

В основе этого уравнения лежит закон сохранения массы. Элемент объема жидкости (dx dydz) располагается в произвольной точке x, у, z потока (рис. 19,1, а). Состояние жидкости и свойства переноса в точке (x, у, z) обозначим через Т, р, ρ, μ,. Ско­рость потока W в координатах х, у, z выразим через ее проек­ции. w_x w_y w_z на оси х, у, z (рис. 19.1).

Пусть плотность жидкости постоянна р=const, тогда масса жидкости в объеме dxdydz должна сохраняться постоянной как при стационарном (скорость потока W не изменяется во времени), так и нестационарном режиме течения. Результирующий массовый расход жидкости через все шесть граней элементарного объема должен быть равен нулю.

Массовый расход жидкости вдоль осп х в точке х, у, z равен pw_x через единицу площади, а через левую грань элементарного объема (рис. 19.1,6) равен pw_xdydz. Разность массовых расхо­дов жидкости через две грани, перпендикулярные оси х, или скорость накопления (расхода) массы в элементе dxdydz через указанные грани равна

Аналогичные результаты для осей у и z:

Уравнение сплошности для потока жидкости при ρ=const полу­чим, приравнивая нулю сумму массовых расходов через все шесть граней элемента

Для потока жидкости с переменной плотностью разность между скоростью прихода массы в элемент и скоростью ухода массы из элемента равна скорости накапливания (расхода) массы элементом объема dxdydz, т. е.

Уравнение (19.2) называют уравнением сплошности. Уравнение (19.2) в векторной форме имеет вид

Вектор pW представляет собой поток массы, и его диверген­ция (div) есть скорость растекания (вытекания) на единицу объема.

Уравнение (19.2) устанавливает, что уменьшение плотности жидкости в элементе объема равно отношению скорости ее выте­кания из элемента к объему элемента.

Основное уравнение теории теплопроводности (уравнение Фурье) и его физический смысл. Краевые условия (условия однозначности). Краевые условия 1-ого, 2-ого, 3-его рода.

В основе уравнения энергии лежит закон сохранения энергии. Рассмотрим элемент массы, мгновенно занимающий объем с центром в точке х, у, z (рис. 19.4, а, б).

Элемент массы проходит через точку х, у, z со скоростью W. Скорость изменения температуры определяется полной производ­ной в форме

(19.10)

Скорость изменения накопленной в элементе энергии (скорость накапливания) является произведением теплоемкости с, массы ρ dx dy dz и скорости изменения температуры (19.10), т. е.

(19.11)

Скорость накапливания энергии должна быть равна скорости прихода энергии через все шесть граней элемента.

Скорость прихода энергии за счет теплопроводности опреде­ляется по закону Фурье. Плотность теплового потока в элемент в направлении оси x равна q_x =-λ∂T/∂x. Скорость прихода энергии за счет теплопроводности в направлении оси х

(19.12)

Соотношения, аналогичные (19.12), могут быть получены для скорости прихода энергии в направлении осей у и z.

Сумма трех скоростей прихода энергии по осям х, у к z уста­навливается равной скорости накапливания энергии в элементе по (19.11), т.е.

(19.13)

Уравнение (19.13) называют уравнением энергии.

Принимаем в (19.13) w_x = 0, w_y= 0_, w_z=0 а также постоян­ным коэффициент λ и, вводя обозначение а=λ/(cρ), где a — темпе­ратуропроводность (м²/с), получим уравнение нестацио­нарной теплопроводности в изотропном твердом теле (при отсутствии источников стоков теплоты)

Уравнение (19.14) называют уравнением теплопровод­ности Фурье. Решением этого уравнения является распреде­ление температуры в пространстве и времени — температурное поле

T = f(x, у, z. τ). Если температура твердого тела не изменяется по времени дТ/ди = 0 то (19.14) примет вид

где ² — оператор Лапласа; последнее уравнение называют урав­нением Лапласа.

Для исследования (расчета) конкретных процессов теплообмена нужно сформулировать и решить краевую задачу, которая должна содержать уравнения сплошности, движения и энергии плюс крае-вые условия или условия однозначности, Задать краевые условия — значит сформулировать, во-первых, начальные условия (значения искомых функций в указанных уравнениях в началь­ный момент времени т-0), во-вторых, граничные. условия на поверхностях, ограничивающих движущуюся жидкость.

Для уравнений сплошности и движения граничные условия определяются для каждой задачи, но общими для всех задач будут два следующих: первое—составляющая скорости жидкости, нормальная к поверхности твердого тела (непроницаемого), равна нулю на поверхности раздела жидкости и твердого тела; второе — при течении сплошной среды, для которой применимы указанные выше уравнения, составляющая скорости жидкости, направленная по касательной к поверхности раздела жидкости и твердого тела, также принимается равной нулю. Считается, что жидкость не скользит при соприкосновении с поверхностью, а «прилипает» к поверхности.

К уравнению энергии для искомой, функции—температуры —

1) граничные условия первого рода, когда задают значения температуры на ограничивающих жидкость поверхностях; в общем случае температура на границе может зависеть от координат точек границы и времени;

2) граничные условия второго рода, когда на поверхности задана плотность теплового потока, т, е. производная от темпе­ратуры по нормали к поверхности (в виде функции времени и координат точек поверхности);

3) граничные условия третьего рода, в которых тепловой поток предполагается пропорциональным разности температур стенки и жидкости:

в этом условии должен быть задан коэффициент теплоотдачи а, а также температура среды T_f,

через граничные условия устанавливается зависи­мость течения жидкости от формы и размеров (диаметра трубы, толщины пластины и т. д.) твердого тела, взаимодействующего с потоком.

Решение задачи опредиления темпратурного поля однослойной плоской стенки при стационарном режиме граничных условиях певого рода. Многослойная плоская стенка. Тепловой поток через однослойную и многослойную стенку

Условия задачи должны содержать уравнение теплопроводности в форме

и граничные условия, например, первого рода:

T=T₁ при x=0 (21.3a)

T=T₂ при x=δ (21.3б)

Представим (21.2) в форме

и после первого интегрирования получим

второе интегрирование дает общее решение уравнения (21.2)

где C₁ и С₂—произвольные постоянные, которые определяют, используя граничные условия (21.3).

Полагая в (21.4) х=0 и используя (21.За), получим

T₁=C₂ (21.5)

а при x=δ на основании (21.36) и (21.4) имеем

откуда

Частное решение уравнения (21.2) при граничных условиях (21.3) с учетом (21.4), (21.5) и (21.6) имеет вид

Из (21.7) видно, что Т(х) линейно зависит от x.

Плотность теплового потока q (рис. 21.1) может быть определена из закона Фурье

или в данном случае

Дифференцируя распределение температуры по толщине стенки (21,7). Получим

откуда

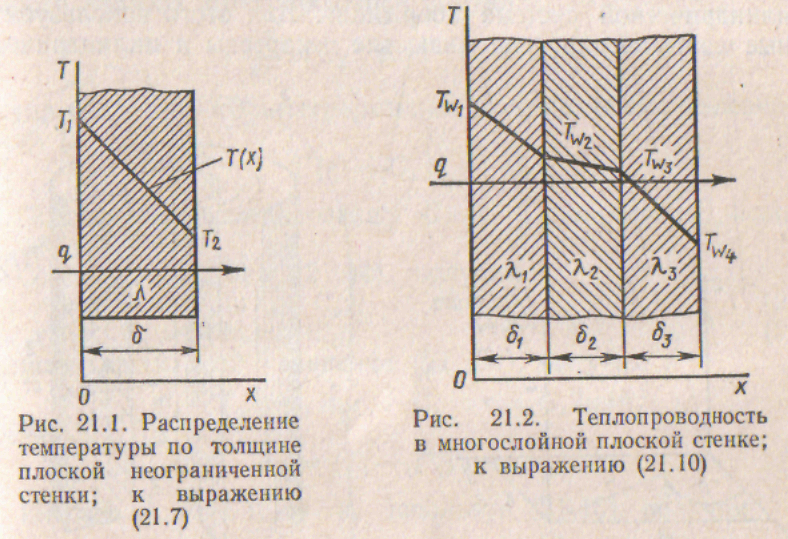
Из (21.8) видно, что при T₁ > T₂ плотность теплового потока положительна, т. е. поток направлен в положительном иаправлении оси х. При T₁< T₂ он будет направлен в обратную

сторону. Количество теплоты, переданное через стенку в единицу времени, вычисляется с помощью (21.8)

где А—площадь поверхности стенки, м².

Определим плотность теплового потока через трехслойную стенку (рис. 21.2); для этого вначале определим термическое сопротивление для каждого слоя (§ 18.1):

Стожим почленно полученные соотношения, в результате получим

откуда

На основании последнего соотношения для многослойной стенки , получим

Решение задачи опредиления темпратурного поля однослойной цилиндрической стенки при стационарном режиме граничных условиях певого рода. Многослойная цилиндрическая стенка. Тепловой поток через однослойную и многослойную стенку

Условия задачи должны содержать уравнение теплопроводности в форме

и граничные условия, например, первого рода:

при r=r₁ T=T₁ (21.13а)

при r=r₂ T=T₂. (21.136)

Представим (21.12) в форме

и после первого интегрирования получим

откуда после второго интегрирования получим общее решение урав­нения (21,12):

Постоянные интегрирования C₁ и С₂ определим, используя (21.13) и (21.14).

Совмещая (21.13) и (21.14), получим

при r=r₁ T₁=C₁lnr₁+C₂ (21.15a)

при r=r₂ T₂=C₁lnr₂+C₂. (21.156)

Вычитая из (21.156) уравнение (21.15а), получим

Найдем С₂ из (21.15а) и, используя (21.16), получим

Решение краевой задачи - частное решение уравнения (21.12) при граничных условиях (21.15) получим, подставляя значения С₁ (21.16) и С₂ (21.17) в общее решение (21.14)

Искомое распределение температуры по толщине цилиндрической стенки (21.18) логарифмически зависит от координаты r,

Плотность теплового потока q определяется из закона Фурье. На основании (21.18) имеем

Количество теплоты, проходящее сквозь цилиндрическую стенку, отнесенное к единице длины трубы, можно определить по формуле

Естественно, что Q не зависит от r, так как теплота нигде не аккумулируется.

Многослойная цилиндрическая стенка. Термическое сопротив­ление многослойной цилиндрической стенки (рис. 21.5) равно сумме сопротивлений отдельных слоев. На основании этого утверж­дения и используя формулу (21.19), можно написать уравнение для определения количества теплоты, проходящего сквозь много­слойную цилиндрическую стенку:

где q_l отнесено к единице длины стенки; п—число слоев.