13. Метод двух узлов, как частный случай метода узловых потенциалов.

Метод двух узлов (МДУ) — метод расчета электрических цепей, в котором за искомое принимают напряжение между 2 узлами схемы. С его помощью определяют токи ветвей.

Порядок расчета:

1. Напряжение между 2 узлами: .

2. Ток в любой ветви: .

Пример:

, , , , , .

, , , — ?

;

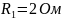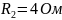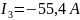14

14. Метод эквивалентного генератора, определение эквивалентного генератора, последовательность и примеры расчёта методом эквивалентного генератора.

Метод эквивалентного генератора (МЭГ) — метод преобразования электрических цепей, в котором схемы, состоящие из неск. ветвей с ЭДС, приводятся к одной ветви с эквив. значением.

Эквивалентный генератор — активный двухполюсник (часть цепи, генерирующая энергию).

По теореме об ЭГ: .

Порядок расчета:

1. Выделяется ветвь с искомым током. Остальная часть схемы условно заменяется ЭГ (независимо от сложности).

2. Находится напряжение на зажимах двухполюсника (в режиме ХХ). Сопротивление нагрузки в расчет не входит, т. к. ветвь разомкнута.

3. Схема делается пассивной — источники ЭДС закорачиваются, ветви с источниками тока размыкаются. Находится эквив. сопротивление (может понадобиться преобраз. треугольник–звезда).

4. Вычисляется искомое значение тока.

1.

2. .

4. .

15, 16

15. Передача энергии от активного двухполюсника, условие передачи максимальной мощности от активного двухполюсника к нагрузке.

Двухполюсник — электрическая цепь (многополюсник), содержащая 2 точки для соединения с другими цепями. Содержащий источник энергии — активный, не содержащий — пассивный.

— мощность, создаваемая активным двухполюсником.

— мощность, потребляемая пассивным двухполюсником.

[Энергетич. характеристики передачи энергии от активного двухполюсника к пассивному (приемнику) на переменном токе зависят от соотношения параметров приемника и источника.]

Согласно МЭГ: если нагрузка подключена к активному двухполюснику, ток в ней: .

Мощность, выделяемая в нагрузке: .

Если взять производную от этого выражения приравнять к 0, получится, что .

Условие передачи максимальной мощности нагрузке: равенство внутренних сопротивлений активного и пассивного двухполюсников.

16. Величины, характеризующие синусоидальный ток или напряжение: частота, период, амплитуда, начальная фаза, средняя за полпериода величина, её соотношение с амплитудой, действующее значение, его соотношение с амплитудой.

Частота (переменного тока) — число полных колебаний тока за секунду: .

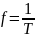Угловая частота — скорость изменения аргумента синусоидальных функций , , .

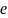Период — время между 2 последовательными прохождениями тела через одно положение.

Амплитуда — максимальное (по модулю) значение мгновенной величины, которое периодически повторяется, причем знак значения чередуется.

Начальная фаза — начальное состояние (тока).

Мгновенное значение — знач. тока в момент времени, функция которого — .

Действующее значение — величина постоянного тока, действие которого совершит ту же работу, что и переменный ток за время одного периода. Иногда используется матем. определение этой величины — среднеквадратичное значение силы переменного тока.

Действующее значение: .

Действующее знач. тока меньше его амплитуды в раз (для синусоид. тока): .

[Среднее значение — постоянная составляющая напряжения / тока.]

Среднее значение синусоидальной величины за период нулевое (один период положит., другой отриц.). Поэтому среднее значение имеет смысл считать за полпериода: .

17

17. Представление синусоидально изменяющихся величин векторами на комплексной плоскости, понятие комплексной амплитуды, комплекса действующего значения, оператора вращения, связь между положением вектора комплексной амплитуды на комплексной плоскости и мгновенным значением синусоидально изменяющейся величины.

Волновые диаграммы не всегда удобны для исследования, #, при сложных разветвленных цепях. В этом случае удобнее представлять синусоидальные величины вращающимися векторами на комплексной плоскости.

Точке на пл-ти соотв. число: (алг. форма).

Показат. форма: . , .

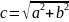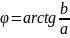, аналогично и .

При расчетах цепей синусоидального тока целесообразно вести расчеты в комплексной форме.

Комплексная амплитуда — величина, модуль и аргумент которой равны амплитуде и начальной фазе гармонического сигнала. Комплексная амплитуда тока: .

Комплекс действующего значения — значение за длительный период времени.

Оператор вращения — парам. , вращающий в-р на относительно начального положения.

18