
- •Микроэлектронные структуры и их строение
- •2. Тепловые свойства структур
- •3. Ионные процессы в диэлектриках
- •4. Электропроводность металлов
- •Распределение Ферми – Дирака
- •Коэффициент пропорциональности между скоростью дрейфа и напряжённостью электрического поля получил название подвижности носителей
- •4.2. Пример решения задач.
- •4.3. Задачи.
- •4.4. Контрольные вопросы.
- •5. Физика полупроводников
- •5.1. Теоретические сведения
- •5.1.1. Собственные полупроводники
- •5.1.2. Примесные полупроводники
- •5.2. Пример решения задач
- •5.3. Задачи
- •Электрона у дна зоны проводимости;
- •Вероятность появления дырки на верхнем уровне валентной зоны при 300к и 50к;
- •5.4. Контрольные вопросы.
- •6. Контактные явления.
- •6.1. Краткие теоретические сведения.
- •6.2. Пример решения задач
- •6.3. Задачи.
- •6.4. Контрольные вопросы.
- •7. Физические эффекты
- •7.1. Теоретические сведения
- •7.1.1. Фотопроводимость полупроводников
- •7.1.2. Эффект Холла
- •7.1.3. Эффекты сильного поля
- •7.1.4. Эффект Ганна
- •7.1.5. Термоэлектронная ионизация Френкеля
- •7.1.6. Ударная ионизация
- •7.1.7. Эффект Зенера
- •7.2. Пример решения задач
- •7.3. Задачи
- •7.4 Контрольные вопросы.
5.1.2. Примесные полупроводники
Для примесного полупроводника донорного типа для возбуждения и переброса в зону проводимости электронов с донорных уровней (рис. 5.2) требуется энергия (Eс-Eд) примерно в 100 раз меньше, чем (Eс-Ev).
Поэтому концентрация электронов в зоне проводимости nn будет равна концентрации дырок на донорных уровнях pд . Если концентрация примесных атомов равна Nд , то концентрация дырок на примесных уровнях равна
|
(5.14) |
Валентная зона
Ts Tί
|
Рис. 5.2 |
В области малых температур заселённость уровней невелика, поэтому функцию распределения Ферми – Дирака можно заменить на функцию Максвелла – Больцмана. Тогда
|
(5.15) |
Приравнивая выражения (5.5) и (4.15), что выражает условие электронейтральности, получаем выражение для энергии уровня Ферми для электронного полупроводника
|
(5.16) |
Из этого выражения следует, что при Т = 0 К уровень Ферми примесного электронного полупроводника располагается посередине между дном зоны проводимости и донорным уровнем.
Если выражение (5.16) подставить в (5.6), получим концентрацию электронов в примесном электронном полупроводнике (основные носители)
|
(5.17) |
где
![]() – энергетический зазор между примесным
донорным уровнем и дном зоны проводимости.
– энергетический зазор между примесным
донорным уровнем и дном зоны проводимости.
Если выражение (5.16) подставить в (5.9), получим концентрацию дырок в примесном электронном полупроводнике (не основные носители)
|
(5.18) |
Перемножая (5.17) и (5.18) и сравнивая с (5.13), находим произведение концентраций основных и не основных носителей в электронном полупроводнике
|
(5.19) |
Выражение (5.19) обусловливает термодинамическое равновесие в полупроводнике и называется законом действующих масс. Из него следует, что с повышением концентрации донорной примеси и, следовательно, с ростом концентрации основных носителей наблюдается при постоянной температуре пропорциональное уменьшение концентрации не основных носителей так, что их произведение остаётся постоянным и равным квадрату концентрации электронов в чистом полупроводнике. Закон действующих масс справедлив для любого невырожденного полупроводника в условиях термодинамического равновесия.
Подставляя в (5.16) значение Nc из (5.6), получаем
|
(5.20) |
||
Если |
|
что выполняется в области |
|
низких температур, уровень Ферми с повышением температуры поднимается вверх ко дну зоны проводимости (рис. 5.2). При дальнейшем повышении температуры второй член выражения (5.20) становится отрицательным, что соответствует снижению уровня Ферми. При температуре Ts он пересекает донорные уровни, что соответствует переходу всех электронов с примесных уровней в зону проводимости (истощение примесных уровней), т.е.
|
(5.21) |
Подставляя это значение nn в выражение (5.17), получаем значение температуры истощения примеси
|
(5.22) |
где ΔE – энергетический зазор между примесным уровнем и дном зоны проводимости. Оценка температуры истощения примесей для германия даёт значение Ts около 32 К.
Выше Ts уровень Ферми понижается примерно пропорционально температуре. В этой области температур начинается возбуждение электронов из валентной зоны. При этом увеличивается как концентрация электронов (ni), так и концентрация дырок в валентной зоне (pi), вследствие чего при ni >> nn значение уровня Ферми определяется выражением (5.12) и располагается в середине запрещённой зоны, совпадая с уровнем Ферми беспримесного полупроводника.
Аналогичные зависимости наблюдаются и в дырочном полупроводнике, в котором имеются только акцепторные уровни (рис. 5.3). При низких температурах концентрация дырок в валентной зоне равна концентрации электронов на акцепторных уровнях. Концентрация электронов на акцепторных уровнях при низких температурах равна
|
(5.23) |
Из условия na = pp получаем выражение для определения уровня Ферми
|
(5.24) |
Подставляя (5.24) в (5.5), получаем концентрацию дырок в дырочном полупроводнике
|
(5.25) |
где ΔEа – энергетический зазор между примесным акцепторным уровнем и потолком валентной зоны.
Подставляя (5.24) в (5.6), получаем концентрацию электронов – не основных носителей заряда (np); сопоставляя np, pp (5.25) и ni (5.12), получаем выражение закона действующих масс для дырочного полупроводника
|
(5.26) |
E Зона проводимости
Eс
+ + + + Eа
Валентная зона 0 T Ts Tί
|
Рис. 5.3 |
При Т = 0 К уровень Ферми в дырочном полупроводнике расположен между акцепторным уровнем и потолком валентной зоны (выражение 5.24). В области низких температур Na>Nv (5.15) и уровень Ферми при повышении температуры сначала опускается к потолку валентной зоны, затем (когда
|
становится отрицательной величиной) он повышает- |
ся, пресекает акцепторный уровень при температуре истощения примеси Ts и стремится при дальнейшем повышении температуры к уровню Ферми для собственного полупроводника, поскольку концентрация собственных носителей значительно превосходит концентрацию акцепторов (рис. 5.3).
На рис. 5.4 представлены температурные зависимости концентрации основных и не основных носителей, построенные по выражениям (5.18), (5.17) и (5.25). Из рисунка видно, что в области низких температур резко возрастает концентрация основных носителей (nn и pp).
Когда все примесные уровни будут ионизированы, концентрация носителей в полупроводнике будет постоянной и равной концентрации соответствующей примеси. При определённой температуре начинается переход собственных электронов из валентной зоны в зону проводимости, что сопровождается увеличением концентрации не основных носителей. Начиная с некоторой температуры, количество междузонных переходов оказывается настолько велико, что концентрации основных и не основных носителей сравниваются и совпадают с концентрацией носителей в собственном полупроводнике.

Рис. 5.4.
Если в полупроводнике одновременно присутствуют донорные и акцепторные примеси, то в соответствии с принципом минимальной энергии электронов будет происходить их перераспределение между донорными и акцепторными уровнями. При Nд>Nа электроны с донорных уровней переходят на акцепторные уровни, которые в этом случае не могут уже принимать электроны из валентной зоны; оставшиеся на донорных уровнях электроны обеспечивают полупроводнику проводимость n – типа. При Nа>Nд на акцепторные уровни переходят не только все электроны с донорных уровней (при Т=0 К), но и электроны из валентной зоны (при Т>0 К), что обусловливает проводимость p – типа. Указанные эффекты получили название компенсации. При Nа=Nд имеет место полная компенсация, вследствие чего концентрация электронов и дырок равна их концентрации в собственном полупроводнике.

 .
. E
E Зона
проводимости
Зона
проводимости


 Eс
Eс



 +
+ + + +
EД
+
+ + + +
EД

 Ev
Ev
 0
T
0
T
 .
. ,
,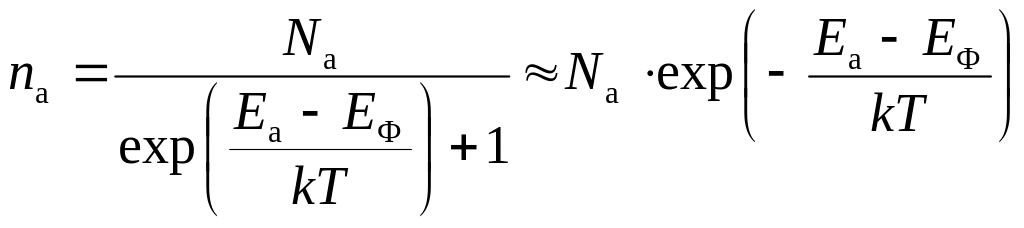 .
.

 +
+
+
+
Ev
+
+
+
+
Ev