
- •Микроэлектронные структуры и их строение
- •2. Тепловые свойства структур
- •3. Ионные процессы в диэлектриках
- •4. Электропроводность металлов
- •Распределение Ферми – Дирака
- •Коэффициент пропорциональности между скоростью дрейфа и напряжённостью электрического поля получил название подвижности носителей
- •4.2. Пример решения задач.
- •4.3. Задачи.
- •4.4. Контрольные вопросы.
- •5. Физика полупроводников
- •5.1. Теоретические сведения
- •5.1.1. Собственные полупроводники
- •5.1.2. Примесные полупроводники
- •5.2. Пример решения задач
- •5.3. Задачи
- •Электрона у дна зоны проводимости;
- •Вероятность появления дырки на верхнем уровне валентной зоны при 300к и 50к;
- •5.4. Контрольные вопросы.
- •6. Контактные явления.
- •6.1. Краткие теоретические сведения.
- •6.2. Пример решения задач
- •6.3. Задачи.
- •6.4. Контрольные вопросы.
- •7. Физические эффекты
- •7.1. Теоретические сведения
- •7.1.1. Фотопроводимость полупроводников
- •7.1.2. Эффект Холла
- •7.1.3. Эффекты сильного поля
- •7.1.4. Эффект Ганна
- •7.1.5. Термоэлектронная ионизация Френкеля
- •7.1.6. Ударная ионизация
- •7.1.7. Эффект Зенера
- •7.2. Пример решения задач
- •7.3. Задачи
- •7.4 Контрольные вопросы.
Коэффициент пропорциональности между скоростью дрейфа и напряжённостью электрического поля получил название подвижности носителей
|
(4.32) |
Из (4.32) получаем общее выражение для удельной электропроводности проводника
|
(4.33) |
которое для случая полупроводника, содержащего электроны и дырки, имеет вид
|
(4.34) |
где n и p – концентрация электронов и дырок,
un и up – их подвижность.
Если предположить, что в результате соударения за время τ полностью теряется приобретенная до этого дрейфовая скорость, то среднюю скорость дрейфа электрона можно выразить как
|
(4.35) |
где
![]() представляет собой ускорение электрона
во внешнем электрическом поле ε. Из
(4.35) получаем другое выражение для
подвижности электронного газа
представляет собой ускорение электрона
во внешнем электрическом поле ε. Из
(4.35) получаем другое выражение для
подвижности электронного газа
|
(4.36) |
При расчётах обычно вводится средняя длина свободного пробега электрона λ, связанная с τ соотношением
|
(4.37) |
где v – средняя скорость движения электронов.
Численная оценка выражений (4.36) и (4.37)
показывает, что, например, для меди
![]()
![]() .
Последняя величина намного порядков
ниже скорости хаотического движения
электронов (
.
Последняя величина намного порядков
ниже скорости хаотического движения
электронов (![]() ).
В то же время
).
В то же время
![]() что примерно в 100 раз превышает величину
межатомного расстояния в меди.
что примерно в 100 раз превышает величину
межатомного расстояния в меди.
Подставляя (4.36) и (4.37) в (4.33), получаем уравнение
|
(4.38) |
которое выражает удельную электропроводность проводника через микроскопические параметры, характеризующие электронный газ. В связи с этим состояние электронного газа будет определенным образом влиять на его электропроводность.
Для невырожденного газа электроны практически не взаимодействуют друг с другом, вследствие чего при наложении внешнего поля каждый электрон принимает участие в электропроводности. Поэтому в выражения (4.36) и (4.38) должны входить усредненные по всему коллективу характеристики, т.е.
|
(4.39) |
|
(4.40) |
Для вырожденного газа возбуждение испытывают только электроны, расположенные вблизи уровня Ферми (фермиевские электроны), поэтому выражения (4.36) и (4.38) приобретают следующий вид
|
(4.41) |
|
(4.42) |
где n – полная концентрация электронов.
Рассмотрим температурные зависимости подвижности носителей, для чего оценим зависимость от температуры средней длины свободного пробега λ и скорости электрона v (выражения (4.39) и (4.41)).
Подвижность носителей заряда определяется их рассеянием. В монокристалле с бездефектной структурой наблюдается рассеяние электронов за счёт взаимодействия с ионами кристаллической решетки, которое тем больше, чем интенсивнее тепловые колебания ионов. Систему колеблющихся ионов кристаллической решетки представляют в виде фононного газа, концентрация фононов в котором определяется выражением
|
(4.43) |
где Eкр – энергия кристаллической решетки;
Eср.ф – средняя энергия фонона
Из курса физики известно, что Eкр и Eср.ф зависят от температуры. В области низких температур (T<<θ)
|
(4.44)
|
откуда
|
(4.45) |
В области высоких температур (T≥θ)
|
(4.46) |
откуда
|
(4.47) |
Во всех этих выражениях θ – характеристическая температура Дебая, при которой тепловые колебания ионов достигают максимальной частоты, а следовательно, и максимальной энергии.
В области высоких температур λ ~ 1/nф (nф – концентрация фононов); так как из (4.46) следует, что nф ~ Т, то λ ~ Т -1. Если для невырожденного газа v ~ T 0,5, то
|
(4.48) |
Для вырожденного газа энергия, а следовательно, и скорость фермиевских электронов практически не зависят от температуры, поэтому
|
(4.49) |
В области низких температур основное значение имеет рассеяние на ионизированных примесных атомах. Расчёты показывают, что длина свободного пробега электронов пропорциональна v 4, поэтому подвижность электронов для невырожденного газа
|
(4.50) |
и для вырожденного газа
|
(4.51) |
Если одновременно действуют несколько механизмов рассеяния, то вводят величину ŵ = 1/τ , представляющую собой среднее число столкновений электрона за единицу времени. Полное число столкновений определяется суммой столкновений, обусловленных различными механизмами рассеяния: электрон – фононным ŵ ф , электрон –примесным ŵ n , электрон– дефектным ŵ д и т.д.
ŵ = ŵ ф + ŵ n + ŵ д . |
(4.52) |
Используя (4.41), получаем
|
откуда
|
(4.54) |
где u ф, u n, u д – подвижности, обусловленные различными механизмами рассеяния электронов. Из (4.54) видно, что основным в определении подвижности является механизм рассеяния, обусловливающий наиболее низкую подвижность.
Электропроводность металлов и сплавов
Концентрация электронов в металлах велика и практически не зависит от температуры (4.16). Поэтому зависимость удельной электропроводности от температуры металлов, как это следует из (4.33), определяется температурной зависимостью подвижности электронного газа, представляющего в данном случае вырожденную систему. Для чистых металлов во всем температурном диапазоне наблюдается один механизм рассеяния электронов – рассеяние на фононах.
В области высоких температур подвижность электронов пропорциональна Т -1 (см. 4.49). Поэтому
|
(4.55) |
а удельное сопротивление
|
(4.56) |
где α – температурный коэффициент сопротивления.
В области низких температур длина
свободного пробега обратно пропорциональна
концентрации фононов nф,
которая равна ~Т3 (4.45). Однако при
низких температурах энергия электрона
теряется не за одно столкновение, а за
![]() столкновений, т.е. эффективная средняя
длина свободного пробега равна λэфф
=
λ.
Расчёты показывают, что
~T
2, поэтому λэфф
~ T
-5. поэтому имеем
столкновений, т.е. эффективная средняя
длина свободного пробега равна λэфф
=
λ.
Расчёты показывают, что
~T
2, поэтому λэфф
~ T
-5. поэтому имеем
|
(4.57)
|
Температурная зависимость удельного сопротивления беспримесного бездефектного металла достаточно точно описывается выражением (4.57) – кривая 1.
Если в металле присутствуют примесные атомы или структура металла имеет дефекты (которые могут быть введены путём деформирования металла), то включаются дополнительные механизмы рассеяния (4.52), вследствие чего общее удельное сопротивление сплава может быть представлено в виде
= ф + п + Д |
(4.58) |
где ρф, ρn, ρд – компоненты удельного сопротивления, обусловленные электрон – фононным, электрон – примесным, электрон – дефектным механизмами рассеяния электронов (рис. 4.5, кривые 2,3).
Деформиро- 3 ванный 3 ρ Cu + 1.12%Nc сплав 2 ρn 1 Чистая медь ρт T, К
|
Рис. 4.5 |
Соотношение (4.58) получило название правила аддитивности удельного сопротивления (правило Матиссена).
Для сплавов ρn обычно значительно превышает ρф поэтому температурный коэффициент удельного сопротивления (ТКС) сплава, как правило, ниже ТКС чистого металла. Это обстоятельство является основой получения константана и манганина – сплавов на основе меди с очень малым ТКС, которые используют для изготовления прецизионных проволочных резисторов.

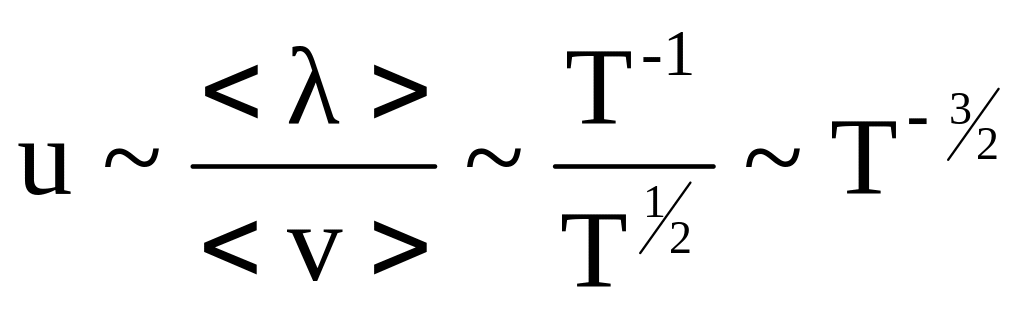 .
. ρ(10
-8
) Ом ∙
м
ρ(10
-8
) Ом ∙
м