
- •Микроэлектронные структуры и их строение
- •2. Тепловые свойства структур
- •3. Ионные процессы в диэлектриках
- •4. Электропроводность металлов
- •Распределение Ферми – Дирака
- •Коэффициент пропорциональности между скоростью дрейфа и напряжённостью электрического поля получил название подвижности носителей
- •4.2. Пример решения задач.
- •4.3. Задачи.
- •4.4. Контрольные вопросы.
- •5. Физика полупроводников
- •5.1. Теоретические сведения
- •5.1.1. Собственные полупроводники
- •5.1.2. Примесные полупроводники
- •5.2. Пример решения задач
- •5.3. Задачи
- •Электрона у дна зоны проводимости;
- •Вероятность появления дырки на верхнем уровне валентной зоны при 300к и 50к;
- •5.4. Контрольные вопросы.
- •6. Контактные явления.
- •6.1. Краткие теоретические сведения.
- •6.2. Пример решения задач
- •6.3. Задачи.
- •6.4. Контрольные вопросы.
- •7. Физические эффекты
- •7.1. Теоретические сведения
- •7.1.1. Фотопроводимость полупроводников
- •7.1.2. Эффект Холла
- •7.1.3. Эффекты сильного поля
- •7.1.4. Эффект Ганна
- •7.1.5. Термоэлектронная ионизация Френкеля
- •7.1.6. Ударная ионизация
- •7.1.7. Эффект Зенера
- •7.2. Пример решения задач
- •7.3. Задачи
- •7.4 Контрольные вопросы.
Распределение Ферми – Дирака
Функция распределения Ферми – Дирака определяет среднее число частиц, подчиняющихся принципу Паули, в данном энергетическом состоянии, т.е. она выражает вероятность заполнения данного состояния:
|
(4.12) |
Рассмотрим основные свойства функции Ферми – Дирака применительно к электронам в металле. При T = 0 К электроны последовательно занимают все состояния, начиная с наинизшего, соответствующего дну зоны проводимости. Значение функции распределения для всех этих уровней равно единице, при этом последним будет заполнен энергетический уровень, высота которого, отсчитанная от дна зоны проводимости, равна химическому потенциалу EФ = Ф. Этот энергетический уровень получил название уровня Ферми. С учётом этого функцию распределения Ферми – Дирака можно представить в виде
|
(4.13) |
Все энергетические уровни, лежащие выше уровня Ферми, свободны, и для них функция распределения равна нулю (fФ(E>EФ)=0). При повышении температуры часть электронов переходит на более высокие энергетические уровни (E>EФ), в результате чего вероятность заполнения этих уровней увеличивается, а вероятность заполнения энергетических уровней, лежащих ниже уровня Ферми (E<EФ), уменьшается. Графики функции распределения Ферми – Дирака для различных значений температуры представлены на (рис. 4.3).
Используя выражения (4.10) и (4.13), а также понятие об уровне Ферми, определим концентрацию электронов n(E)dE, имеющих энергию в области от E до E+dE,
 (4.14)
(4.14)
Важнейшими свойствами уровня Ферми являются:
Вероятность заполнения электроном уровня Ферми при любой температуре равна ½.
Уровень Ферми представляет собой химический потенциал электронов данной системы (в расчёте на один электрон). Поэтому условием равновесия двух электронных проводников, которые приведены в контакт (безразлично, металлов или полупроводников), является равенство их уровней Ферми.
Уровень Ферми определяется из условия, что независимо от распределения по уровням, полное число электронов в кристалле должно оставаться неизменным. Это требование связано с условием электронейтральности системы в целом.
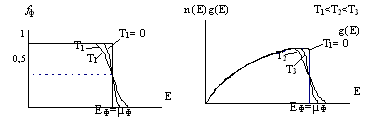
Рис. 4.3
Интегрируя выражение (4.14), получаем общее число частиц в единице объёма системы
|
(4.15) |
что приводится к следующему выражению
|
(4.16) |
откуда получаем
|
(4.17) |
где
|
(4.18) |
представляет собой значение уровня Ферми металлов при 0 К.
Значение
![]() составляет
обычно величину около 5 эВ; поправка в
(4.17) во всём температурном интервале не
превышает сотых долей процента, поэтому
в отличие от полупроводников в металлах
уровень Ферми практически не зависит
от температуры и определяется выражением
(4.18).
составляет
обычно величину около 5 эВ; поправка в
(4.17) во всём температурном интервале не
превышает сотых долей процента, поэтому
в отличие от полупроводников в металлах
уровень Ферми практически не зависит
от температуры и определяется выражением
(4.18).
Из условия
![]() определяем значение ТФ
определяем значение ТФ
|
(4.19) |
выше которой выполняется критерий невырожденности электронного газа. Расчёты показывают, что эта температура примерно на два порядка выше температуры плавления металлов, в связи с чем электронный газ в металлах всегда находится в вырожденном состоянии.
Одной из основных характеристик электронной проводимости является закон дисперсии, выражающий зависимость энергии электрона от импульса p, т.е. Е = Е(р). Для свободных электронов
|
При абсолютном нуле температуры энергия электронов в металле ограничивается энергией Ферми, которой соответствует импульс
|
(4.21) |
Проведя в пространстве импульсов сферу радиусом pФ, получим энергетическую поверхность ЕФ , отделяющую заполненные состояния от незаполненных. Такая изоэнергетическая поверхность называется поверхностью Ферми. Характер этой поверхности определяется видом зависимости Е(р), который лишь в частном случае свободных электронов приводит к сферической поверхности Ферми. Для электронов проводимости в кристалле закон дисперсии имеет более сложный вид, и поверхность Ферми не является сферической.
Поверхность Ферми является наиболее важной характеристикой металлов, позволяющей понять и объяснить его основные свойства: электрические, тепловые, магнитные, механические, оптические.
Анализируя различные функции распределения частиц по энергиям (4.1, 4.8, 4.12), получаем, что при условии
|
(4.22) |
функции Бозе–Эйнштейна и Ферми – Дирака переходят в функцию Максвелла – Больцмана, которую можно рассматривать как предельный случай квантовых статистик.
Условие (4.22) эквивалентно условию
|
(4.23) |
и оба условия определяют критерий вырождения системы частиц.
С учётом (4.7) условие (4.22) можно записать
|
(4.24) |
Так как максимальное значение экспоненциального члена стремиться к 1, то условие (4.24) перепишется в виде
|
(4.25) |
Из (4.25) следует, что степень вырождения системы элементов определяется их концентрацией и температурой: чем больше концентрация элементов и чем ниже температура, тем сильнее вырождена система электронов. Из (4.25) получаем соотношение между концентрацией электронов и температурой системы
|
(4.26) |
При комнатной температуре правая часть выражения (4.26) составляет величину 2,5 1025 м –3. В металлах концентрация свободных электронов практически постоянная и составляет величину порядка 1028м –3, т.е. при комнатной температуре система электронов в металле всегда находится в вырожденном состоянии и поведение электронов описывается только квантовой статистикой Ферми – Дирака.
Электропроводностью называют явление направленного переноса (движения) свободных носителей заряда под действием электрического поля. Необходимым условием существования электропроводности у кристаллов является наличие в их энергетической диаграмме частично заполненных электронами энергетических зон. Только в этом случае электрическое поле может привести к нарушению чисто беспорядочного движения носителей заряда – электронов и дырок, к наложению на него направленного переноса.
В отсутствии внешнего электрического поля электронный газ в проводнике находится в равновесном состоянии и описывается функциями распределения Максвелла - Больцмана (невырожденный газ) или Ферми – Дирака (вырожденный газ). На рис. 4.4 представлены графики распределения функции fМ(vx) и fФ(vx). Симметричность функции указывает на то, что количество электронов, движущихся в противоположных направлениях, одинаково, а средняя скорость их движения
vд
0 vx |
fф vд ε
0 vx |
Рис. 4.4 |
|
равна нулю, что обусловливает отсутствие тока при нулевой напряжённости внешнего электрического поля.
Установление равновесия в электронном газе происходит за счёт взаимодействия электронов с тепловыми колебаниями решётки (фононами) и примесными атомами, искажающими локальные электрические поля. Это взаимодействие приводит к рассеянию электронов и установлению беспорядочного движения их в проводнике.
При наложении внешнего электрического
поля напряжённостью
![]() возникает электрический ток плотностью
возникает электрический ток плотностью
|
(4.27) |
где σ – коэффициент пропорциональности, называемый электропроводностью проводника.
Величина, обратная σ, называется удельным сопротивлением.
|
(4.28) |
Направленное движение электронов называют дрейфом. Так как заряд электрона отрицателен, дрейф происходит в направлении, противоположном .
Рассмотрим в потоке электронов параллелепипед с единичным основанием и высотой равной vд, где vд – средняя скорость дрейфа. Тогда объём параллелепипеда равен vд, число электронов в нём n · vд, где n – концентрация электронов. Пройдя через основание параллелепипеда, эти электроны образуют ток плотностью
|
(4.29) |
где «-» означает, что ток направлен противоположно направлению дрейфа электронов. Сравнивая (4.27) и (2.28), имеем
|
(4.30) |
откуда
|
(4.31) |

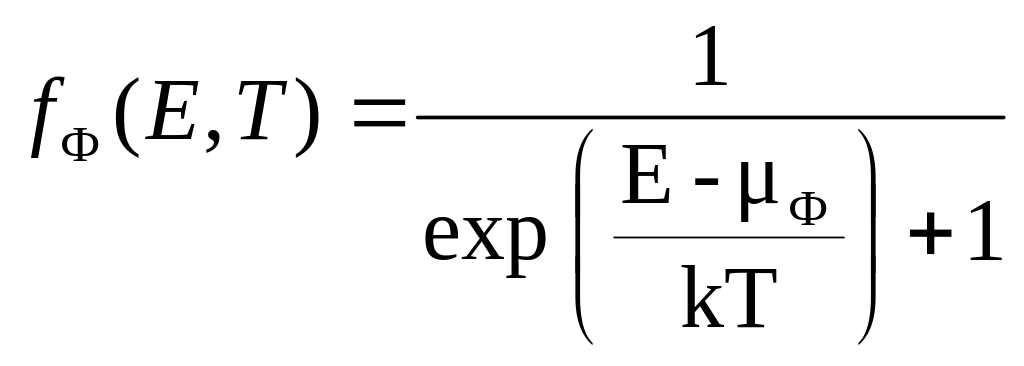 .
. .
. ,
,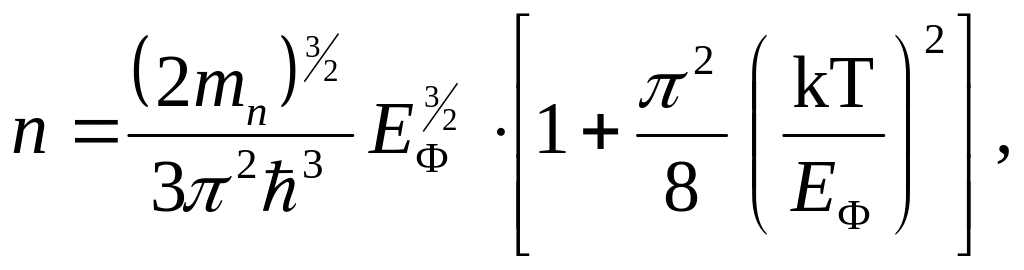

 fм
fм ε
ε
