4. Электропроводность металлов
4.1. Теоретические сведения
В системе большого числа частиц наблюдаются определённые закономерности в отношении распределения этих частиц по энергиям, которые носят название статистических. Эти закономерности описываются статистической функцией распределения f(E,T), зависящей от вида частиц, находящихся в данном энергетическом состоянии E при температуре T.
Предположим, что на N одинаковых частиц приходится G различных состояний, в которых может находиться отдельная частица. Мерой нахождения частицы в данном состоянии служит отношение N/G. Если N/G<<1, то число вакантных состояний много больше числа частиц. Подобные коллективы называются невырожденными и описываются классической статистикой Максвелла - Больцмана.
Если N/G>>1, то свойства частиц определяют заселённость состояний. Такие коллективы частиц получили название вырожденных. Вырожденные коллективы могут образовываться только квантово-механическими частицами. Действительно, для выполнения последнего условия необходимо, чтобы число возможных состояний частиц (G) было бы во всяком случае конечным. Это может быть в том случае, если параметры состояний частицы изменяются дискретно, т.е. если частица является квантово-механическим объектом.
М
ежду
невырожденностью коллектива и
классичностью его членов нет однозначного
соответствия. Невырожденные коллективы
могут образовывать и квантово-механические
объекты, если выполняется условие
N/G<<1.
Статистическая физика, изучающая свойства вырожденных коллективов, называется квантовой статистикой. Различают квантовые статистики Ферми - Дирака и Бозе - Эйнштейна.
Распределение Максвелла – Больцмана
Классические частицы различимы, причём в данном энергетическом состоянии может находиться неограниченное число частиц. Такие частицы (например, молекулярный газ) описываются классической статистикой Максвелла-Больцмана
|
(4.1) |
,где м – термодинамический параметр, называемый химическим потенциалом.
Химический потенциал выражает изменение свободной энергии системы при изменении числа частиц на единицу при неизменной температуре и объёме системы, т.е. химический потенциал равен величине свободной энергии (F), приходящейся на одну частицу системы в состоянии равновесия, и выражается формулой
|
(4.2) |
,где n – число частиц в системе.
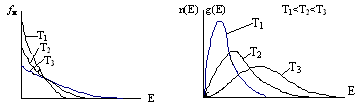
Рис. 4.1
Из графиков функции распределения Максвелла-Больцмана и распределения частиц по энергиям (рис. 4.1) видно, что при уменьшении температуры число частиц с малыми значениями энергии неограниченно возрастает. При температуре абсолютного нуля все частицы займут самое нижнее энергетическое состояние.
Используя (4.1), можно определить концентрацию частиц n(E)dE, находящихся в интервале энергии dE
|
(4.3) |
,где g(E) – плотность энергетических состояний, приходящихся на единицу объёма системы частиц. С учётом (4.1), получаем
|
(4.4) |
.Интегрируя (4.4) по всем значениям энергии, получаем общее число частиц в системе
|
(4.5) |
,откуда получаем значение химического потенциала
|
(4.6) |
.С учётом (4.6) функция распределения Максвелла -Больцмана имеет вид
|
(4.7) |
.Распределение Бозе – Эйнштейна
Функция Бозе – Эйнштейна имеет вид
|
(4.8) |
.В условиях равновесия бозоны имеют минимум свободной энергии, вследствие чего химический потенциал бозонов
|
(4.9) |
Поскольку для бозонов (фотонов и фононов) энергия
E = h, то с учётом (4.9) получаем функцию распределения Бозе – Эйнштейна в виде
|
(4.10) |
.Используя выражение (4.10) и значение энергии бозонов (E= h), получаем распределение бозонов по частотам
|
(4.11) |
.Из графиков функции распределения Бозе – Эйнштейна и распределения частиц по энергиям (рис. 2.3) следует, что с уменьшением температуры число бозонов с малыми значениями энергий уменьшается; уменьшается также и общее число бозонов.
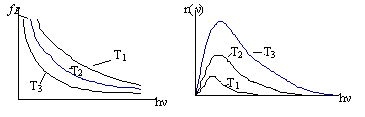
Рис. 4.2