Оглавление

Введение 5 1. Микроэлектронные структуры и их строение 6 1.1. Краткие теоретические сведения 6 1.2. Примеры решения задач 8 1.3. Задачи 8 1.4. Контрольные вопросы 10 2. Тепловые свойства структур 11 2.1. Краткие теоретические сведения 11 2.2. Примеры решения задач 16 2.3. Задачи 17 2.4. Контрольные вопросы 18 3. Ионные процессы в диэлектриках 19 3.1. Краткие теоретические сведения 19 3.2. Примеры решения задач 21 3.3. Задачи 22 3.4. Контрольные вопросы 24 4. Электропроводность металлов 25 4.1. Теоретические сведения 25 4.2. Примеры решения задач 44 4.3. Задачи 45 4.4. Контрольные вопросы 47 5. Физика полупроводников 49 5.1. Теоретические сведения 49 5.1.1. Собственные полупроводники 49 5.1.2. Примесные полупроводники 53 5.2. Примеры решения задач 60 5.3. Задачи 60 5.4. Контрольные вопросы 64 6. Контактные явления 65 6.1. Краткие теоретические сведения 65 6.2. Примеры решения задач 67 6.3. Задачи 68 6.4. Контрольные вопросы 70 7. Физические эффекты 72 7.1. Теоретические сведения 72 7.1.1. Фотопроводимость полупроводников 72 7.1.2. Эффект Холла 77 7.1.3. Эффект сильного поля 81 7.1.4. Эффект Ганна 83 7.1.5. Термоэлектронная ионизация Френкеля 88 7.1.6. Ударная ионизация 91 7.1.7. Эффект Зенера 92 7.2. Примеры решения задач 94 7.3. Задачи 95 7.4. Контрольные вопросы 96 Библиографический список 98

Введение

Углубление взаимной связи фундаментальной науки и технического воплощения новых идей и открытий, ускорение и интенсификация процесса такого взаимного проникновения и обогащения являются объективной закономерностью развития отраслей, удовлетворяющих информационные потребности общества. Поэтому каждый инженерно – технический работник должен знать основные физические законы, составляющие теоретический фундамент функционирования приборов, устройств и систем, т.е. той техники, творцом которой он призван быть.

Данные методические указания к практическим занятиям призваны помочь студентам изучить физические процессы, которые широко проявляются и используются при производстве и эксплуатации микроэлектронной аппаратуры, а также призваны служить выработке навыков самостоятельной работы, необходимых для дальнейшей исследовательской работы.

Задачи и вопросы данного пособия сгруппированы по разделам, охватывающим теоретический материал курса «Физические основы микроэлектроники». К задачам основных разделов даны предварительные краткие теоретические сведения и указания. При этом предполагается, что студент знакам с соответствующим теоретическим материалом, а математическая подготовка, необходимая для решения задач, не выходит за пределы обычного курса интегрального и дифференциального исчисления.

1. Микроэлектронные структуры и их строение

1. Краткие теоретические сведения

Под термином «кристаллическая решетка» понимают твердую фазу вещества, расположение атомов или молекул в которой проявляет определенную закономерность хотя бы на микроскопических участках. При этом наименьший объем, путем трансляции которого можно полностью воспроизвести структуру кристалла, называется элементарной ячейкой.

Элементарная ячейка имеет размеры a, b, c по направлению осей x, y, z. Любой узел кристаллической решетки может быть выбран в качестве начала координат для элементарной ячейки.

Кристаллографическое направление в решётке [mnp] определяется координатами атома m, n, p ближайшего к началу координат и лежащего на данном направлении. Если угол между направлениями [m₁n₁p₁] и [m₂n₂p₂] обозначить через , то

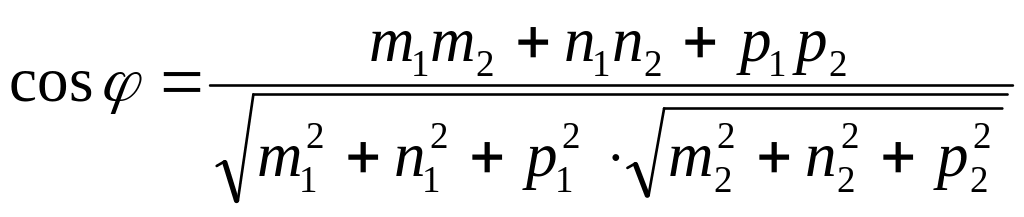. (1.1)

Для описания плоскости в кристалле необходимо знать отрезки, отсекаемые плоскостью по осям в выбранной системе координат – m, n, p по осям х, у и z соответственно, тогда уравнение плоскости в отрезках будет иметь вид

(1.2)

или после приведения к общему знаменателю

, (1.3)

где h,k,l – целые числа, называемые индексами Миллера.

Решетка содержит множество идентичных плоскостей, которые обозначаются фигурными скобками hkl. Скол, например, происходит по определенным плоскостям решетки, поверхностная плотность узлов в которых наибольшая.

Межплоскостное расстояние для кристаллов кубической сингонии определяется по формуле

, (1.4)

где а - параметр решетки.

Чем выше индексы плоскостей, тем ближе эти плоскости расположены друг к другу. Угол между плоскостями (h₁k₁l₁) и (h₂k₂l₂) в кристаллах кубической сингонии определяется из соотношения:

. (1.5)

Если известен химический состав кристалла и определена его кристаллическая структура, то можно вычислить период решётки этого кристалла:

, (1.6)

где М – масса моля вещества;

N_А – число Авогадро;

ρ – плотность вещества.

Равновесная концентрация вакансий (дефектов Шоттки) при данной температуре (Т) определяется по формуле Больцмана

, (1.7)

где n – число атомов в единице объёма;

е – основание натурального логарифма;

k – постоянная Больцмана;

E_ш – энергия образования вакансий.

Равновесная концентрация дефектов Френкеля определяется по формуле

, (1.8)

где n_м – число возможных межузельных положений на единицу объёма;

E_ф – энергия образования дефекта Френкеля.

Для большинства кристаллов энергия образования вакансий примерно равна 1 эВ, а энергия образования внедрений равна 3 – 5 эВ.

2. Пример решения задач

Задача. Плоскость пересекается с осями координат в точках x = 1,5а; у = 3а; z = 2а, где а – параметр элементарного куба кристаллической решётки. Определить индексы Миллера этой плоскости.

Решение.

Уравнение плоскости в отрезках куба будет иметь вид:

приводя к общему знаменателю, получим

следовательно, искомая плоскость в индексах Миллера запишется (4 2 3).

3. Задачи

1. В кубической кристаллической решётке постройте плоскости с индексами Миллера (1 2 1) и (1 ).

2. Определить расстояние между ближайшими параллельными плоскостями {1 1 1} в кубической кристаллической решётке с периодом «а» элементарной ячейки.

3. Сколько атомов располагается на 1 мм² плоскости (1 0 0) и (1 1 1) ГЦК решётки с межатомными расстоянием а = 3,499Å?

4. Определить плотность упаковки объёмно-центрированной кубической решётки с радиусом атома R. Покажите, что .

5. У каких плоскостей в структурах ОЦК и ГЦК наибольшая плотность упаковки атомов? В каких направлениях в этих плоскостях линейная плотность расположения атомов максимальна?

6. Вычислить постоянную решётки «а» для KCl по числу Авогадро и плотности, равной 1990 кг/м³.

7. Расстояние между ближайшими атомами в кристаллической решётке равно 0,2737 нм. Известно, что вольфрам имеет структуру объёмно-центрированного куба. Найти плотность материала.

8. Определить концентрацию свободных электронов в натрии, элементарная ячейка которого представляет собой объёмно-центрированный куб с ребром а = 0,428 нм.

9. При температуре, на 10К меньшей температуры плавления алюминия (Т_пл = 933К) на долю вакансии приходиться 0,08% мест в кристаллической решётке, а при 484 ºС – только 0,01% мест. Чему равна энергия Е образования одной вакансии?

10. Образец алюминия быстро охлажден от температуры, близкой к температуре плавления (932К), и все вакансии, имеющиеся в нём при высокой температуре. Будет повышаться или падать плотность Al в процессе отжига вакансий? Можно ли измерить это изменение с помощью существующей экспериментальной техники?

1.4. Контрольные вопросы

1. Что представляет собой кристаллическое состояние вещества?

2. Какие вы знаете типы кристаллических решёток?

3. Чем отличается идеальный кристалл от реальных кристаллов?

4. Что представляют собой индексы Миллера?

5. Как определить индексы Миллера узла кристаллической решётки, направления в кристалле и плоскости?

6. Как изменяется концентрация вакансий и внедрений в кристалле с изменением температуры?

7. Как определить угол между двумя направлениями в решетке с кубической сингонией?

8. Как определить угол между двумя плоскостями в решетке с кубической сингонией?

9. Почему кристаллы раскалываются по определенным плоскостям?

10. Доказать, что в кубическом кристалле любое направление [mnp] перпендикулярно плоскости (hkl), если m=h, n=k, p=l.