
- •3. Электропроводность твёрдых тел
- •Коэффициент пропорциональности между скоростью дрейфа и напряжённостью электрического поля получил название подвижности носителей
- •3.2. Электропроводность металлов и сплавов
- •3.3. Электропроводность полупроводников
- •3.4. Эффект Холла
- •3.5. Эффекты сильного поля
- •Контрольные вопросы
3.4. Эффект Холла
Эффектом Холла называется явление, состоящее в том, что при пропускании тока вдоль проводящей пластинки, помещённой перпендикулярно линиям внешнего магнитного поля, возникает поперечная разность потенциалов вследствие взаимодействия носителей заряда с магнитным полем.
Если по проводнику, имеющему форму прямоугольной пластинки, протекает электрический ток I (рис. 3.8), то в отсутствие магнитного поля разность потенциалов между мочками С и Д, лежащими на одной из эквипотенциальных поверхностей, равна нулю.
При наложении магнитного поля, индукция
которого
![]() перпендикулярна направлению тока и
плоскости образца, между точками С и Д
возникает разность потенциалов Vx,
называемая холловской э.д.с.
перпендикулярна направлению тока и
плоскости образца, между точками С и Д
возникает разность потенциалов Vx,
называемая холловской э.д.с.
При протекании тока в направлении,
указанном на рис. 3.8 стрелкой, электроны
совершают дрейф со скоростью
![]() в противоположном направлении. На каждый
такой электрон со стороны магнитного
поля действует сила Лоренца
в противоположном направлении. На каждый
такой электрон со стороны магнитного
поля действует сила Лоренца
|
(3.50) |
|
|
a
Д Fл I Vх
|
|
Рис. 3.8 |
|
Так как угол между и равен 90˚, то численное значение Fл составляет
|
(3.51) |
Под действием этой силы электроны отклоняются к внешней стороне пластины, заряжая её отрицательно; на противоположной стороне пластины накапливаются нескомпенсированные положительные заряды. Это приводит к появлению электрического поля
|
(3.52) |
где Vх – холловская э.д.с.
Поле Eх действует на электроны с силой F = -e∙Eх, направленной против силы Лоренца. При F = Fл поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов прекращается. Из этого условия имеем
|
(3.53) |
откуда
|
(3.54) |
Учитывая, что плотность тока в проводнике
![]() ,
получаем из (3.44) значение Холловской
э.д.с.
,
получаем из (3.44) значение Холловской
э.д.с.
|
(3.55) |
где
![]() -
постоянная Холла.
-
постоянная Холла.
Формула (3.55) справедлива только для металлов и вырожденных полупроводников, т.к. только в них электроны обладают близкими энергиями и скоростями (фермиевские электроны). Для невырожденных полупроводников постоянная Холла имеет следующий вид
|
(3.56) |
где А – константа, которая для атомных решёток равна 1,17 при рассеянии носителей на тепловых колебаниях и 1,95 при рассеянии на ионизированных примесях.
Для полупроводников p-типа направление дрейфа носителей заряда совпадает с направлением тока. Сила Лоренца и в этом случае будет направлена от С к Д, т.к. изменяются одновременно и знак заряда и направление дрейфа носителей. Однако сила теперь действует на положительно заряженные частицы, и поэтому точка Д окажется под положительным потенциалом относительно точки С. Следовательно, по знаку холловской э.д.с. можно определить знак носителей заряда в проводнике. Условились считать знак постоянной Холла положительным, когда ток переносится дырками. С учётом этого правила постоянную Холла записывают так:
для полупроводников p-типа с концентрацией дырок, равной p:
|
(3.57) |
для полупроводников n-типа с концентрацией электронов, равной n:
|
(3.58) |
Для полупроводника со смешанной проводимостью, когда концентрации электронов и дырок сравнимы друг с другом, постоянная Холла вычисляется из соотношения
|
(3.59) |
которое переходит в (3.57) при р>>n и в (3.58) при n>>р.
Для собственных полупроводников, в которых n=p=ni соотношение (3.59) приобретает вид
|
(3.60) |
Обычно подвижность электронов выше подвижности дырок, поэтому знак постоянной Холла является, как правило, отрицательным.
Умножая постоянную Холла на удельную
электропроводность проводника
![]() ,
получаем
,
получаем
|
(3.61) |
откуда определяется подвижность заряда.

 I
С
I
С vд
vд


 F
F


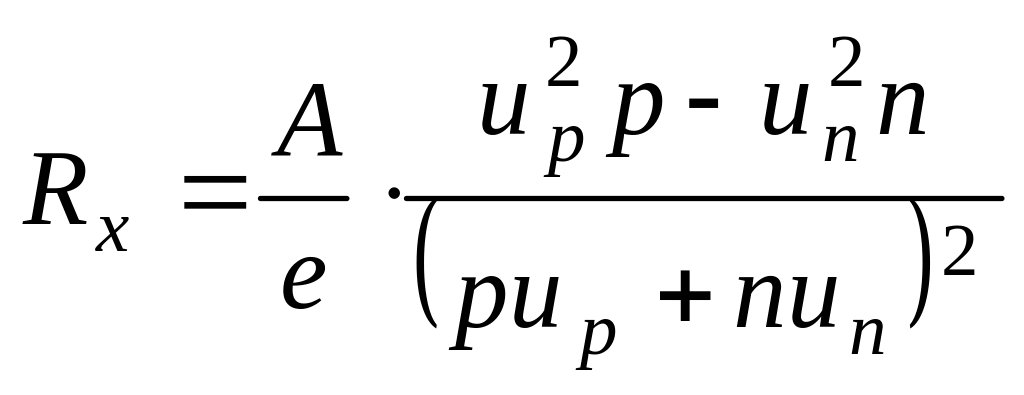 ,
,