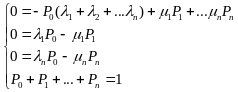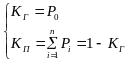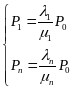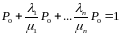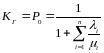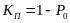- •1. Основные понятия и определения надежности.
- •2. Состояния сложного объекта. Отказ. Восстановление.
- •3. Надежность. Ее составляющие.
- •4. Живучесть. Отказоустойчивость. Гарантоспособность.
- •5.Классификация отказов сложных технических объектов.
- •6.Показатели надежности невосстанавливаемых объектов. Функция и плотность распределения времени безотказной работы, функция надежности
- •7. Показатели надежности невосстанавливаемых объектов. Вероятность безотказной работы и вероятность отказа
- •9.Показатели надежности невосстанавливаемых объектов. Средняя наработка
- •8. Показатели надежности невосстанавливаемых объектов. Интенсивность отказов
- •10. Законы распределения наработки до отказа невосстанавливаемых объектов (ступенчатый, дискретный).
- •11.Законы распр. Наработки до отказа невосст. Объектов (экспон, норм, Вейбулла-Гнеденко, Рэлея).
- •1. Экспоненциальное распределение
- •2. Распределение Вейбула-Гнеденко
- •4. Распределение Релея
- •12. Потоки отказов восстанавливаемых объектов. Способы задания потоков отказов.
- •13. Простейший поток отказов. Его свойства.
- •14. Нестационарный пуассоновский поток.
- •15. Поток Эрланга.
- •16.Показатели надежности восст. Объектов.
- •17.Показатели безотказности восстанавливаемых объектов.
- •18. Показатели ремонтопригодности восст-ых объектов.
- •20. Компл. Показатели надежности восст-ых объектов.
- •21. Расчет показателей надежности объекта при основном соединении его элементов.
- •22. Расчет показателей надежности объекта при резервном соединении его элементов.
- •24,25 Расчет надежности сложного технического объекта при номинальных, заданных условиях эксплуатации.
- •26.Метод перебора состояний. Пример.
- •28.Метод минимальных путей и сечений. Пример.
- •Виды избыточности сложных технических объектов.
- •30*. Классификация структурного резервирования
- •Значения k сокращать нельзя!
- •31. Оценка эффективности резервирования.
- •32. Пост. Общ. Резервирование с целой кратностью. Пример.
- •33. Постоянное общее резервирование с дробной кратностью. Пример.
- •34. Мажоритарное резервирование. Пример.
- •3 5.Постоянное поэлементное резервирование с целой кратностью
- •36. Резервирование замещением. Виды режимов работы резер. Эл-ов. Методы расчета показателей надежности
- •37. Расчет показателей надежности восстанавливаемых объектов методом переходных интенсивностей
- •38. Виды стратегии восстановления. Примеры
- •39. Постоянное общее резервирование с мгновенным замещением отказавшего элемента. "Схема гибели"
- •40. Общее резервирование объекта с восстанавливаемыми элементами. "Схема гибели и размножения".
- •41 Резервирование замещением с восстанавливаемыми элементами и нагруженным режимом работы
- •42 Резервирование замещением с восстанавливаемыми элементами и ненагруженным режимом работы.
- •43. Оптимальное резервирование. Прямая задача
- •44. Оптимальное резервирование. Обратная задача
- •45 Модель поведения сложного объекта со встроенной системой контроля.
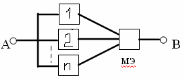
34. Мажоритарное резервирование. Пример.
n |
3 |
5 |
7 |
r |
2 |
3 |
4 |
n
– нечетно всегда, выходные сигналы с
этих элементов подаются на МЭ. Он
сравнивает и выдает сигнал большинства
элементов в схеме. 2 из 3, n=3,
необходимо чтобы 2 были работоспособны.
Слабое место мэ, поэтому
 на 2 – 3 порядка. Как пост общ рез с дроб
крат.
на 2 – 3 порядка. Как пост общ рез с дроб
крат.

Выигрыш:
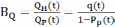 Выигрыш
по Т незначительный, используется в
системах, где нужно обеспечить выс Р на
незначит время эксплуатации.
Выигрыш
по Т незначительный, используется в
системах, где нужно обеспечить выс Р на
незначит время эксплуатации.
П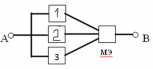 ример:
Опр. вероят. безотказной работы
мажоритарной резервной схемы в течении
1000ч.
ример:
Опр. вероят. безотказной работы
мажоритарной резервной схемы в течении
1000ч.
n=3;
t=1000ч.;  =10-4
1/час;
=10-4
1/час;
мэ=3*10-6 1/час.

 =
=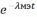 *
*
*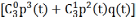 .
.
3 5.Постоянное поэлементное резервирование с целой кратностью
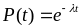
r=1; n=k+1; Pi(t)+qi(t)=1
каждому элементу вводится резервный

Внутри каждой группы рассчитывается по формулам пост. общего резервирования Поэлементное резервирование всегда рассчитывается по формуле общего резервирования.
Ср.
наработка:
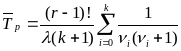
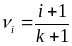
-индекс отказа нерезервированного устройства.
k-кратность резервирования
r- число обязательных функционирующих элем. для правильной работы.
36. Резервирование замещением. Виды режимов работы резер. Эл-ов. Методы расчета показателей надежности

r=1; k; n=k+1 все элементы равнонадежны расчет проводится по всем режимам
Расчет ведется по формулам пост. общего резервир.
Резервирование с замещением:
а) общая с замещением б) постоянная с замещением в) скользящее
По виду режима работы резервного элемента:
1) нагруженный «горячий» режим:
 ;
; 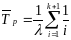
2) облегченный или «теплый»
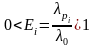 ;
;
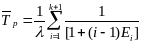
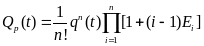
3) ненагруженный или «холодный»
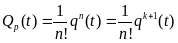
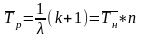
37. Расчет показателей надежности восстанавливаемых объектов методом переходных интенсивностей
Время безотказной работы и время восстан-я подчинены экспоненц. закону. tв<<t; t – непрерывное. Потоки отказов обладают след. свойствами: стационарный, ординарный и без последействия. Системы с этими свойствами наз-ся Марковскими. Для анализа надежности таких систем исп. диф. ур-ия первого порядка 0-работоспособное сост. 1-состояние отказа(восст-ия). Тогда
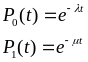
 -интенсивность
потока отказа=const
-интенсивность
потока отказа=const
 -интенсивность
потока восстановления
-интенсивность
потока восстановления
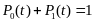

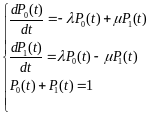 Уравнения
Колмагорова-Чепмена. Число этих ур-ий
= числу состояний.
Уравнения
Колмагорова-Чепмена. Число этих ур-ий
= числу состояний.
Для составления ур-ий К-Ч составляется граф сост. объекта, граф ориентированный
0
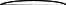
λ
1

µ
При решении сист. можно найти:
1) вер-ть любого состояния Pj(t)
2)ф-цию
- Кг(t)=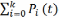 и коэф. - Kг=
и коэф. - Kг=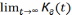 готовности
готовности
3)ф-цию
- Кп(t)=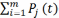 и коэф. - Kп=
и коэф. - Kп=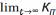 (t)
простоя
(t)
простоя
Кп(t) + Кг(t)=1
38. Виды стратегии восстановления. Примеры
Каждый элемент после отказа восстанавливается. 2 модели:
1)после отказа любого элемента сист. отказывает, элемент ставится на восстановление, остальные не работают (откл.)
2)после отказа любого элемента сист. отказывает, отказавший элемент ставится на восстановление, все ост. элементы продолжают работать и могут отказать. В итоге, когда включается отказавший элемент, система может не заработать. Для 2-ой модели есть 3 модификации:
а) неограниченное восстановление. m=n. n-кол-во элементов в схеме. m-эл-ты, котор. могут быть поставлены на восстан-е
б) частично ограниченное восстановление, m<n
в) полностью ограниченное восстановление. Т.е. на восстановл. может находиться только 1 элемент.
Граф для первой модели восстановления
всего
состояний n+1.
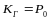
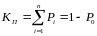
С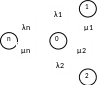 оставляем
ур-ие К-Ч. Решаем ее с помощью метода
финальных вероятностей
оставляем
ур-ие К-Ч. Решаем ее с помощью метода
финальных вероятностей
Предположим что вероятности от времени не зависят, производные обращаются в 0.