- •1. Понятие качества нового продукта
- •2.2.2. Закон нормального распределения
- •2.2.3. Закон распределения Вейбулла
- •2.2.4. Критерий согласия Пирсона
- •2.2.5. Точность и надежность оценок числовых характеристик
- •3.2. Зависимость надежности системы от надежности элементов
- •3.3. Пример выполнения лабораторной работы № 2
- •3.4. Надежность работы элементов конструкции по критерию усталостной прочности
- •3.5. Применение статистических методов подобия к определению усталостных характеристик деталей машин
- •3.6. Пример выполнения лабораторной работы № 3 «Исследование
- •3.8 . Пример выполнения лабораторной работы №4
3.8 . Пример выполнения лабораторной работы №4
«Надежность соединения с натягом»
Задание на лабораторную работу
Зубчатое
колесо закреплено со сплошным валом
диаметром 48мм прессовой посадкой с
натягом
 (отверстие диаметром 48
(отверстие диаметром 48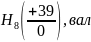 диаметром 48
диаметром 48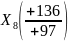 ).
Соединение нагружено вращающим моментом
T
, заданным нормально распределенной
величиной со средним значением T
1500
).
Соединение нагружено вращающим моментом
T
, заданным нормально распределенной
величиной со средним значением T
1500
 и коэффициентом вариации
и коэффициентом вариации
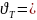 0,12.
Определить вероятность безотказной
работы соединения по критерию сцепления
деталей. Дано: диаметр ступицы зубчатого
колеса
0,12.
Определить вероятность безотказной
работы соединения по критерию сцепления
деталей. Дано: диаметр ступицы зубчатого
колеса
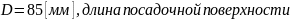 l
l ,
модуль упругости материала E
,
модуль упругости материала E средне
значение аоэфициента трения
средне
значение аоэфициента трения
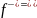 0,12,
коэффициент вариации коэффициента
трения
0,12,
коэффициент вариации коэффициента
трения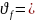 0,075,
коэффициент K
0,075,
коэффициент K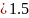 уменьшения со временем давления в
соединении.
уменьшения со временем давления в
соединении.
Выполнение лабораторной работы
Среднее
значение натяга
и
коэффициента вариации в зависимости
от допусков вала и отверстия
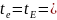 39
39 ,а
также нижнего отклонения вала ei
,а
также нижнего отклонения вала ei
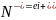 0,5(
0,5( ,
,
 0,0948.
0,0948.
Поправка на обмятие микронеровностей
U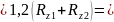 1,2(4+6)=12
1,2(4+6)=12
Коэффицент
 =1,936
=1,936
Среднее значение давления на посадочной поверхности
126,7 МПА.
Коэффициент
вариации

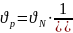 =0,108.
=0,108.
Среднее значение и коэффициент вариации предельного по прочности сцепления момента
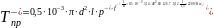
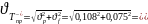 0,132.
0,132.
Средний коэффициент запаса прочности
 .
.
Квантиль
По таблице Приложение 4) по квантили определяем вероятность безотказной работы
P(t) 0, 980
Вероятность безотказной работы системы с натягом «вал-ступица шестерни» по критерию сцепления высокая.
Приложение 1
Значения
функции Лапласа Ф(x)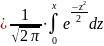 Таблица П-1
Таблица П-1
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
||||||||
0.0 |
0.00 |
004 |
008 |
012 |
0159 |
020 |
024 |
028 |
032 |
036 |
|
|
|
||||||||
0.1 |
039 |
044 |
048 |
052 |
056 |
057 |
063 |
067 |
071 |
075 |
|
|
|
||||||||
0.2 |
079 |
083 |
087 |
091 |
095 |
099 |
103 |
106 |
110 |
114 |
|
|
|
||||||||
0.3 |
118 |
122 |
126 |
129 |
133 |
136 |
141 |
144 |
148 |
152 |
|
|
|
||||||||
0.4 |
155 |
159 |
163 |
166 |
170 |
174 |
177 |
181 |
184 |
188 |
|
|
|
||||||||
0.5 |
191 |
195 |
198 |
202 |
205 |
209 |
212 |
216 |
219 |
222 |
|
|
|
||||||||
0.6 |
226 |
229 |
232 |
236 |
239 |
242 |
245 |
249 |
252 |
255 |
|
|
|
||||||||
0.7 |
258 |
261 |
264 |
267 |
270 |
273 |
276 |
279 |
282 |
285 |
|
|
|
||||||||
0.8 |
288 |
291 |
294 |
297 |
299 |
302 |
305 |
308 |
311 |
313 |
|
|
|
||||||||
0.9 |
316 |
319 |
321 |
324 |
326 |
329 |
331 |
334 |
336 |
339 |
|
|
|
||||||||
1.0 |
341 |
344 |
346 |
349 |
351 |
353 |
355 |
358 |
360 |
362 |
|
|
|
||||||||
1.1 |
364 |
367 |
369 |
371 |
373 |
375 |
377 |
379 |
381 |
383 |
|
|
|
||||||||
1.2 |
385 |
387 |
389 |
391 |
393 |
394 |
396 |
398 |
400 |
401 |
|
|
|
||||||||
1.3 |
403 |
405 |
407 |
408 |
410 |
411 |
413 |
415 |
416 |
418 |
|
|
|
||||||||
1.4 |
419 |
421 |
422 |
424 |
425 |
426 |
428 |
430 |
431 |
432 |
|
|
|
||||||||
1.5 |
433 |
434 |
436 |
437 |
438 |
439 |
441 |
442 |
443 |
444 |
|
|
|
||||||||
1.6 |
445 |
446 |
447 |
448 |
450 |
451 |
452 |
453 |
454 |
454 |
|
|
|
||||||||
1.7 |
455 |
456 |
457 |
458 |
459 |
460 |
461 |
462 |
462 |
463 |
|
|
|
||||||||
1.8 |
464 |
465 |
466 |
466 |
467 |
468 |
469 |
469 |
470 |
471 |
|
|
|
||||||||
1.9 |
471 |
472 |
473 |
473 |
474 |
474 |
475
|
476
|
476 |
477 |
|
|
|
||||||||
2.0 |
477 |
478 |
478 |
479 |
479 |
480 |
480
|
481
|
481 |
482 |
|
|
|
||||||||
2.1 |
482 |
483 |
483 |
483 |
484 |
484 |
485 |
485 |
485 |
486 |
|
||||||||||
2.2 |
486 |
486 |
487 |
487 |
487 |
488 |
488 |
488 |
489 |
489 |
|||||||||||
2.3 |
489 |
490 |
490 |
490 |
490 |
491 |
491 |
491 |
491 |
492 |
|||||||||||
2.4 |
492 |
492 |
492 |
492 |
493 |
493 |
493 |
493 |
493 |
494 |
|||||||||||
2.5 |
494 |
493 |
494 |
494 |
494 |
494 |
495 |
495 |
495 |
495 |
|||||||||||
2.6 |
495 |
495 |
496 |
496 |
496
|
496 |
496 |
496 |
496 |
496 |
|||||||||||
2.7 |
496 |
497 |
497 |
497 |
497
|
497 |
497 |
497 |
497 |
497 |
|||||||||||
2.8
|
497 |
497 |
498 |
498 |
498
|
498
|
498
|
498
|
498
|
498
|
|||||||||||
2.9 |
498 |
498 |
498 |
498 |
498 |
498 |
498 |
498 |
498 |
498 |
|||||||||||
|
|
|
|||||||||||||||||||
X |
|
3.0 |
3.5 |
4.0 |
|
|
|
||||||||||||||
Ф(x) |
0.49865 |
0.49977 |
0.499968 |
|
|||||||||||||||||
Приложение 2.
Значения в зависимости от r и . Таблица П-2
r |
0.95 |
0.90 |
0.80 |
0.70 |
0.50 |
0.30 |
0.20 |
0.10 |
0.05 |
1 |
0.004 |
0.016 |
0.064 |
0.148 |
0.455 |
1.074 |
1.642 |
2.71 |
3.84 |
2 |
0.103 |
0.211 |
0.446 |
0.713 |
1.386 |
2.41 |
3.22 |
4.60 |
5.99 |
3 |
0.352 |
0.584 |
1.005 |
1.424 |
2.37 |
3.66 |
4.64 |
6.25 |
7.82 |
4 |
0.711 |
1.064 |
1.649 |
2.20 |
3.36 |
4.88 |
5.99 |
7.78 |
9.49 |
5 |
1.145 |
1.610 |
2.34 |
3.00 |
4.35 |
6.06 |
7.29 |
9.24 |
11.07 |
6 |
1.635 |
2.20 |
3.07 |
3.83 |
5.35 |
7.23 |
8.56 |
10.64 |
12.59 |
7 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
8 |
2,73 |
3,49 |
5,53 |
7,34 |
9,52 |
11,03 |
11,03 |
13,36 |
15,51 |
9 |
3,32 |
4,17 |
5,38 |
6,39 |
8,34 |
10,66 |
12,24 |
14,68 |
16,92 |
10 |
3,94 |
4,86 |
6,18 |
7,27 |
9,34 |
11,78 |
3,44 |
15,99 |
1831 |
11 |
4,58 |
5,58 |
6,99 |
8,15 |
1034 |
12,90 |
14,63 |
17,28 |
19,68 |
12 |
5,23 |
6,30 |
7,81 |
9,03 |
11,34 |
14,01 |
15,81 |
18,55 |
21,00 |
13 |
5,89 |
7,04 |
8,63 |
9,93 |
12,34 |
15,12 |
16,98 |
19,81 |
22,4 |
14 |
6,57 |
7,79 |
9,47 |
1082 |
13,34 |
16,22 |
18,15 |
21,1 |
23,7 |
15 |
7,26 |
8,55 |
1031 |
11,72 |
14,34 |
17,32 |
19,31 |
22,3 |
25,0 |
Приложение 3.
Лабораторная работа № 1. Статистическая обработка результатов исследования.
1.По
результатам испытаний, приведенных
индивидуально для каждого студента
или группе 2…3 человека в виде протокола
первичной статистической совокупности
составить таблицу группированного
статистического ряда, указать число
событий
в каждом разряде, частоту
,
плотность частоты
 (x).
(x).
2.
Построить график статистической функции
распределения
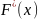 и гистограмму.
и гистограмму.
3.
Определить приближенные значения
статистических вероятностных
характеристик:
,
 ,
,
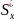 .
.
4.
Выполнить задачу выравнивания
статистического материала с помощью
закона нормального распределения,
приняв вероятностные характеристики
 гипотетического закона равными
соответствующим статистическим
характеристикам. Построить графики
функции распределения F(x) и плотности
вероятностей f(x) непрерывного
распределения.
гипотетического закона равными
соответствующим статистическим
характеристикам. Построить графики
функции распределения F(x) и плотности
вероятностей f(x) непрерывного
распределения.
5.
Определить критерий согласия
Пирсона и вероятность
соответствия гипотетического
распределения статистическому. За
порог значимости принять,
 0,3.
0,3.
6.
Установить, какова вероятность того,
что ошибка от замены статистических
характеристик
и
на характеристики
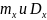 гипотетического
распределения не превзойдет заданных
значений
гипотетического
распределения не превзойдет заданных
значений
 .
.
Данные для исследования. Таблица П-3
№ вар. |
Первичная статистическая совокупность |
|
|
|
1 |
4,10, 11, 40, 35, 44, 52, 25, 38, 51,19, 28, 32, 18, 29, 17, 40,16, 53, 54, 31, 33, 47, 48, 26, 27, 47, 49, 33, 39, 35, 36, 27, 28, 29, 44, 48, 15, 19, 42, 43, 37, 38, 39, 33, 31, 38, 39, 33,31, 38, 39, 32, 31, 27, 26, 30, 24, 23, 8. |
4 |
28 |
|
2 |
62, 51, 41, 32, 28, 29, 35, 42, 53, 63, 64, 54, 45, 36, 38, 25,31, 44, 52, 61, 44, 43, 47, 55, 56, 65, 48, 49, 42, 45, 59, 43, 44, 49, 47, 42, 41, 39, 31, 34, 22, 37, 35, 23, 62, 63, 36, 48, 59, 51. |
5 |
27 |
|
3
|
37, 41, 51, 55, 61, 64, 72, 81, 38, 43, 52, 54, 62, 68, 74, 82, 39, 45, 53, 53, 63, 77, 83, 48, 54, 51, 64, 79, 84, 49, 55, 56, 65, 71, 56, 65, 71, 56, 65, 71, 56, 59, 61, 75, 58, 67, 57, 68, 58, 51, 69, 59, 55, 58, 63. 32, 35, 42,54, 55. |
4 |
30 |
|
4 |
48, 51, 61, 71, 72, 78, 77, 81, 92, 82, 73, 76, 75, 62, 52,49. 53, 63, 64, 74, 75, 76, 83, 93, 85, 77, 78, 65, 56. 66,79, 74, 86 , 95, 87, 73, 72, 68, 57, 59, 69, 71, 73, 88, 96, 54, 75, 77, 89, 50. |
5
|
|
|
40
|
|
|||
5 |
4, 11, 20, 21, 31,41, 32, 22, 11, 12, 5, 13, 12, 23, 33, 42, 34, 24, 25, 13, 14,15, 6, 16,14, 26, 35, 45, 36, 26, 28, 15, 17, 20, 7, 19, 18, 29, 37, 48, 8, 16, 17, 22, 38, 49,23, 18,19,15. |
3
|
26
|
|
6 |
18, 22, 31,39, 41, 49, 45, 51, 61, 19, 23, 32, 38, 42, 48, 47, 52, 62, 24,33, 37, 43, 47, 49, 53, 27, 34, 36, 44, 46, 42, 54, 28, 35, 45, 47, 55, 29, 36, 46, 48, 57, 37, 47, 49, 58, 38, 48, 41, 59.
|
2,7 |
25
|
Приложение 4
Вероятность безотказной работы P(t) в зависимости от квантили нормального распределения. Таблица П-4
|
P(t) |
|
P(t) |
|
P(t) |
0.000 |
0.5000 |
- 1.1 |
0.8643 |
- 2.326 |
0.99 |
- 0.1 |
0.5398 |
-1.2 |
0.8849 |
- 2.4 |
0.9918 |
- 0.126 |
0.55 |
- 1.282 |
0.9 |
- 2.409 |
0.992 |
- 0,2 |
0.5793 |
- 1.3 |
0.9032 |
- 2.5 |
0.9938 |
-0.253 |
0.60 |
- 1.4 |
0.9192 |
- 2.576 |
0.995 |
-0.3 |
0.6179 |
- 1.5 |
0.9332 |
- 2.60 |
0.9953 |
-0.385 |
0.65 |
- 1.6 |
0.9452 |
- 2.652 |
0.996 |
-0.4 |
0.6554 |
- 1.645 |
0.95 |
- 2.7 |
0.9965 |
-0.5 |
0.6915 |
- 1.7 |
0.9554 |
- 2.748 |
0.997 |
-0.524 |
0.7 |
- 1.751 |
0.96 |
- 2.8 |
0997 |
-0.6 |
0.7257 |
- 1.8 |
0.9641 |
- 2.878 |
0.998 |
-0.674 |
0.75 |
- 1.881 |
0.97 |
- 2.9 |
0.9981 |
-0.7 |
0.7580 |
- 2.0 |
0.9772 |
- 3.0 |
0.9986 |
-0.8 |
0.7881 |
- 2.054 |
0.98 |
- 3.090 |
0.999 |
-0.842 |
0.8 |
- 2.1 |
0.9821 |
- 3.291 |
0.9995 |
-0.9 |
0.8159 |
- 2.170 |
0.985 |
- 3.5 |
0.9998 |
-1.0 |
0.8413 |
- 2.2 |
0.9861 |
- 3.719 |
0.9999 |
-1.036 |
0.85 |
- 2.3 |
0.9893 |
- |
- |
Приложение 5.
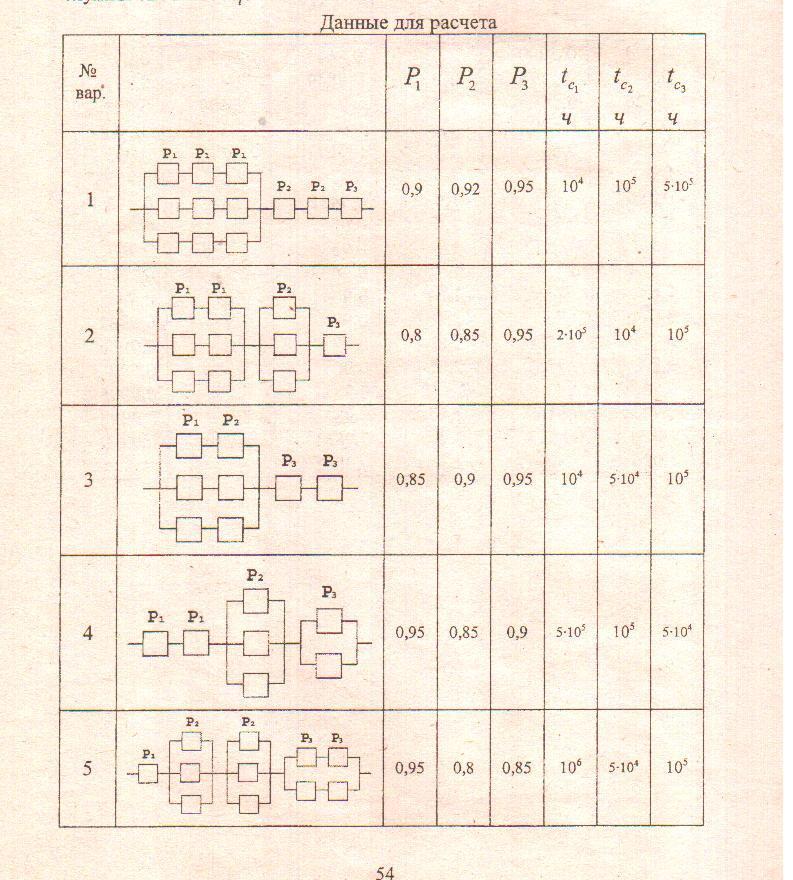
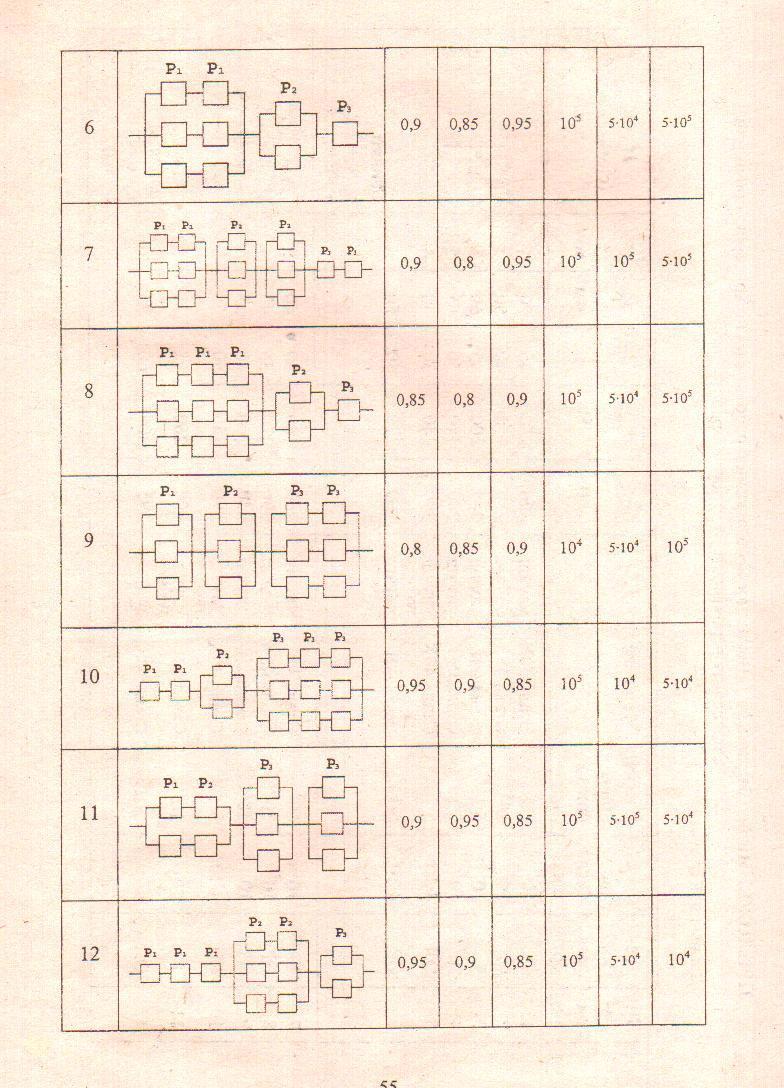
Лабораторная работа № 2. Исследование надежности системы.
Для приведенной в таблице смешанной системы с постоянным резервированием ряда элементов индивидуально установить вероятность безотказной работы P(t).
При известных значениях срока службы отдельных элементов при нормальной эксплуатации установить среднее значение срока службы системы .
Приложение 6.
Лабораторная работа №3. Исследование надежности работы вала по критерию усталостной прочности.
1. Установить вероятность безотказной работы вала P(t) по критерию усталостной прочности.
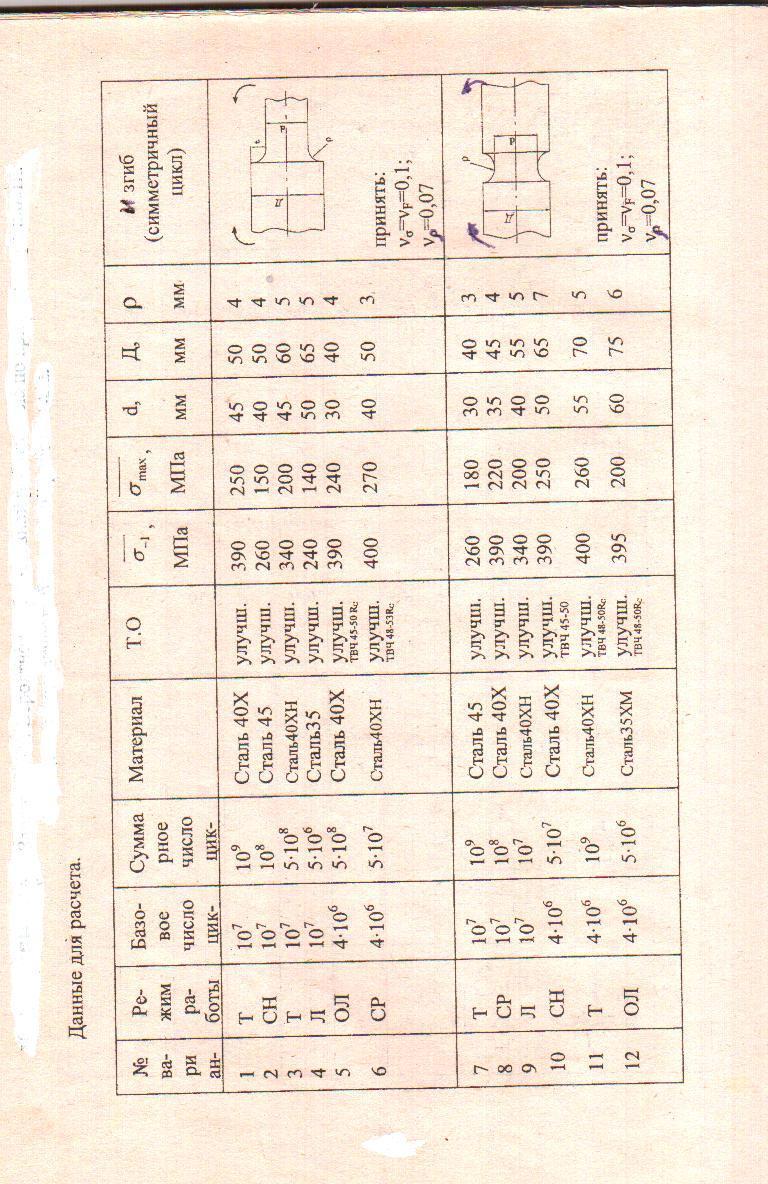
Приложение 7.
Лабораторная работа № 4. Надежность соединения с натягом.
Установить вероятность безотказной работы соединения по критериям сцепления и прочности соединения вала и ступицы (втулки) с натягом.
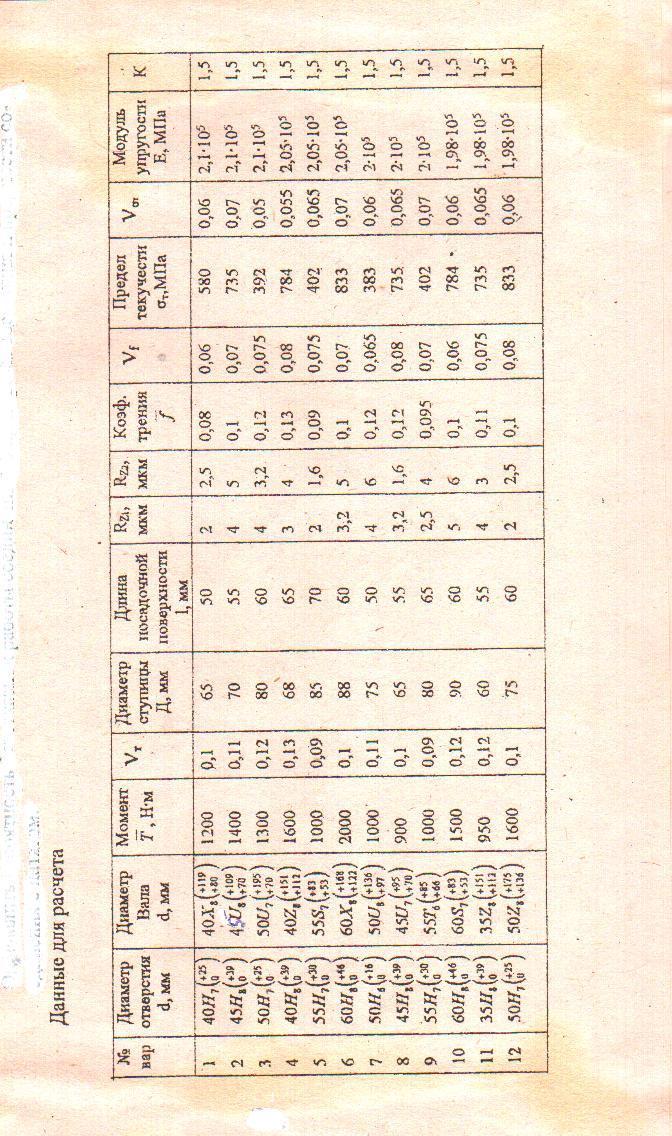
Литература
Аристов О.В. Управление качеством: Учеб.пособие для вузов.-М.: ИНФРА-М, 20004.-240с.
2 Мельников В.П. Управление качеством: Учебник для студ. Учреждений проф. образования/В.П.Мельников, В.П.Смоленцев, А.Г.Схиртладзе; Под ред.В.П.Мельникова.-М.:Издательский центр «Академия», 2005.-352 с.
Шестаков В.Г. Основы теории надежности механических систем. Метод. указ./В.Г.Шестаков.-Барнаул, Изд-во АлтГТУ, 2010.-41 с.