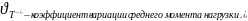3.5. Применение статистических методов подобия к определению усталостных характеристик деталей машин

В связи с высокой стоимостью и длительности усталостных испытаний натурных деталей машин, на усталость испытывают в основном гладкие образцы. Поэтому важное значение приобретают расчетные методы распространения результатов испытаний малых простых образцов на натурные детали. Такие возможности дают статистические теории подобия усталостных разрушений, например, теория Серенсена – Когаева.

Установлено, что на усталостную и хрупкую прочность значительное влияние оказывают размеры детали, вид нагружения и концентраторы напряжения: выточки, галтели, шпоночные пазы, сварные швы, прессовые посадки и т.д. Теории опираются на два предположения: несущие способности элементарных объемов детали независимы друг от друга и отказ детали возникает при разрушении хотя бы одного элементарного объема.

Коэффициент вариации предела выносливости точно изготовленных деталей из материала одной плавки рассматривают как функцию ,где L – часть периметра поперечного сечения детали;

градиент первого главного напряжения в этом сечении. Величина - пропорциональна напряженному объему, в котором возможно зарождение трещины.

Для деталей круглого сечения при изгибе с вращением

L

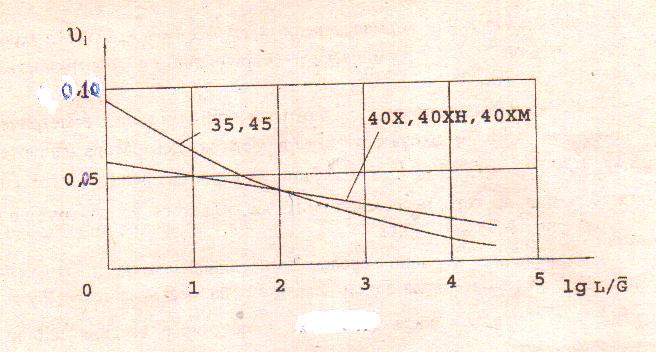
Рисунок 11. Коэффициент вариации

Для ступенчатого вала с диаметрами d и D и галтелью радиуса относительный градиент при изгибе на основе решения теории упругости

, (53)

где при 0; при 1,5, , где .

Для вала с глубокими гиперболическими выточками при изгибе

. (54)

На рисунке 11 приведены графики для , для сталей 35, 45, 40X, 40XH, 40XM в зависимости от lg .

3.6. Пример выполнения лабораторной работы № 3 «Исследование

надежности вала по критерию усталостной прочности».

Необходимо установить вероятность безотказной работы P(t) по критерию усталостной прочности ступенчатого вала, испытывающего циклические нормальные напряжения изгиба по симметричному циклу. Дано: материал – сталь 40X улучшенная (m = 6), режим тяжелый (Т), базовое число циклов суммарное число циклов ,средняя величина предела выносливости 240 Мпа, среднее статистическое максимальное напряжение цикла 100 Мпа, размеры ступенчатого вала с галтелью: d = 35мм, D = 45мм, 3мм. По результатам статистического материала известны коэффициенты вариации: 0,07. По таблице 4 устанавливаем начальный момент, 0,3

0,3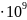 ; 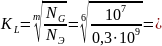0,567 принимается, 1,0.

Коэффициент запаса по средним напряжениям

2,4.

Для определения , определим значения L и

L 3,14 0,931.

При 0,14.

118; 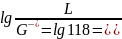2,072.

По графику на рисунке 11 для стали 40X, имеем 0,041. Принимая 0,026, имеем, коэффициент вариации предела выносливости.

0,0598.

Квантиль,

По таблице (Приложение 4) имеем, P(t) 0,9999. Имеем высокую вероятность безотказной работы системы в заданный срок службы.

3.7. Надежность соединения с натягом

Актуальность исследования и расчета соединений с натягом связано с большим рассеянием допусков на натяг, коэффициентов трения, давлений в соединении, внешних нагрузок.

Среднюю величину предельного по прочности сцепления момента , который может передать соединение диаметром d длиной l со средним натягом , при средних давлениях на посадочных поверхностях и среднем коэффициенте трения 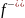, можно подсчитать по следующей формуле

0,5 , (55)

где K 1,5 – коэффициент, учитывающий возможность уменьшения сил сцепления со временем (от местного обмятия и частичного снятия сил трения). Предельный момент рассматривается как функция двух случайных величин p и f.

Среднее давление в соединении сплошного вала со ступицей с наружным диаметром ступицы D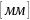 из материала одного с валом модуля упругости E и коэффициена Пуассона

, (56)

где ;

U 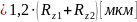– поправка на обмятие посадочных поверхностей, зависящая от высоты их микронеровностей .

Коэффициент вариации предельного момента, коэффициент вариации давления, коэффициент вариации натяга и коэффициент вариации коэффициента трения

;

;

;

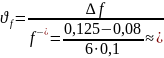0,075,

где ei – допуск на диаметр вала;

допуск на диаметр вала;

допуск на диаметр отверстия;

допуск натяга;

средняя величина натяга;

.

Вероятность безотказной работы соединения по критерию прочности сцепления определяется по таблице (Приложение 4) нормального распределения в зависимости от квантили

, (57)

где -средний коэффициент запаса прочности;