3.3. Пример выполнения лабораторной работы № 2

«Исследование надежности системы»

Индивидуально каждому студенту или группе 2…3 человека в Приложении 5 задается схема смешанной системы, состоящей из последовательных и параллельных элементов с известными характеристиками надежности элементов системы. Необходимо установить вероятность безотказной работы и срок службы всей системы. Резервирование постоянное с нагруженным резервом. В рассматриваем примере для смешенной системы, приведенной на рисунке 9, с известными характеристиками элементов необходимо установить вероятность безотказной работы и срок службы системы . 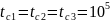Дано: ; ч.; 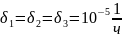. Разбиваем систему на подсистемы (блоки).

Устанавливаем вероятность безотказной работы системы

P(t)

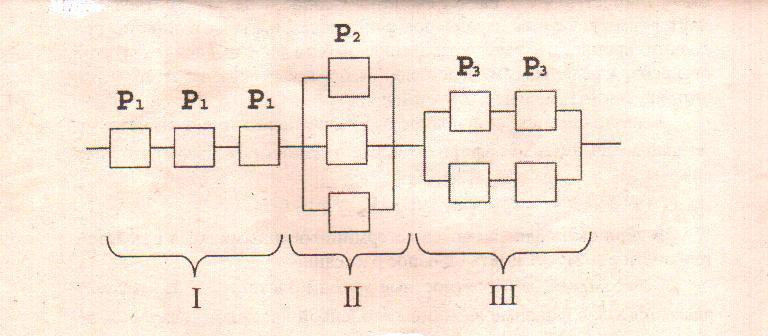
Рисунок 9. Комбинированная (смешанная) система.

Определяем срок службы системы(

Сроки службы блоков:

Интенсивность отказов блоков: ;

.

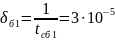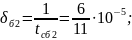
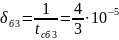Интенсивности отказа системы:

.

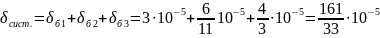Срок службы системы 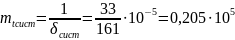ч.

Благодаря введению в систему элементов резервирования вероятность безотказной работы и срок службы всей системы оказались на достаточно высоком уровне.

3.4. Надежность работы элементов конструкции по критерию усталостной прочности

В исследовании элементов конструкции на сопротивление усталости необходимо оценить нагруженность рассматриваемого элемента, которая характеризуется спектром нагрузок. Спектры нагрузок могут быть дискретными или непрерывными.

Для непрерывного спектра нагрузок задается функция плотности распределения f(F) или интегральная функция . Последняя формула физически означает вероятность, что нагрузка меньше данной величины

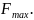
Статистический анализ нагруженности различных типов показал, что их можно свести к нескольким типовым. Функция плотности вероятностей f(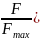 спектров относительных нагрузок для типовых режимов нагружений приведены на рисунке 10. Здесь, кривая 1 – спектр тяжелого режима; кривая 2 – спектр среднего равновероятного режима; кривая 3 – спектр среднего нормального режима; кривая 4 – спектр легкого режима; кривая 5 = спектр особо легкого режима.

Спектры нагрузок задаются их начальными моментами 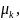где k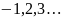 -порядок начального момента.

Начальные моменты k-того порядка определяют по формулам: для дискретных нагрузок

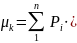; (44)

Для непрерывных нагрузок

. (45)

Начальные моменты отражают основные свойства спектра: среднее значение, рассеяние нагрузки, асимметрию распределения нагрузок.

В расчетах деталей машин на сопротивление усталости теория базируется на гипотезе линейного суммирования повреждений. При определении эквивалентного числа циклов перемен напряжений используют коэффициент эквивалентности циклов , равный начальному моменту к-го порядка 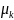, т.е. .

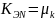При определении эквивалентной нагрузки коэффициент эквивалентности режима нагружения 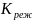устанавливают через начальный момент , где порядок начального момента k совпадает с показателем степени m кривой усталости Веллера . При контактных нагрузках, когда напряжения пропорциональны корню квадратному от нагрузки, порядок начального момента .

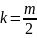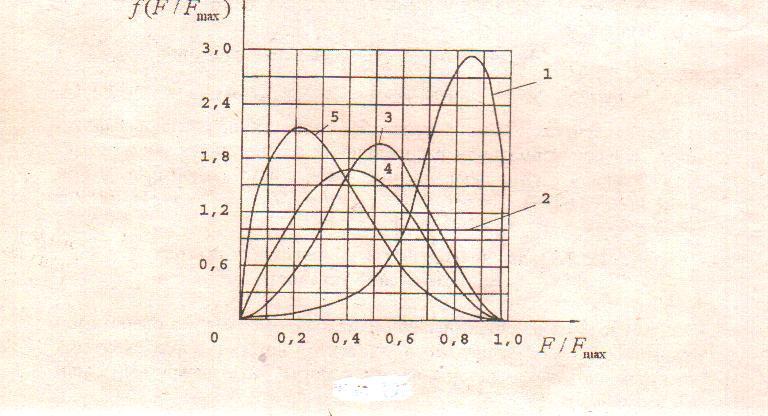
Рисунок 10. Типовые режимы нагружений.

При напряжениях, пропорциональных нагрузкам

, (46)

При контактных нагрузках

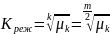. (47)

Значения начальных моментов 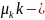го порядка для спектров относительных нагрузок типовых режимов приведены в таблице 4.

В расчетах на сопротивление усталости эквивалентные нагрузки, т.е. нагрузки постоянного режима нагружений, эквивалентного по усталостному воздействию рассматриваемому переменному режиму, находятся как:

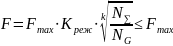, (48)

где 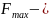максимальная нагрузка спектра;

число циклов до перелома кривой усталости;

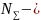суммарное число циклов перемен напряжений за весь срок службы;

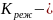коэффициент переменности режима;

k показатель степени,порядок начального момента.

Значения начальных моментов

Таблица 4.

			Порядок начального момента k
Режим
			1		2		3		6		9	12
	Тяжелый (Т)	0,772		0,615		0,501		0,300		0,200			0,142
	Средний равновероятный (СР)	0,5		0,333		0,250		0,143		0,100			0,0769
	Средний нормальный (СН)	0,5		0,286		0,179		0,0651		0,0358			0,0266
	Легкий (Л)	0,423		0,218		0,127		0,0384		0,0164			0,0084
	Особо легкий (ОЛ)	0,310		0,128		0,0622		0,0126		0,0041			0,0017

Коэффициент вариации эквивалентной нагрузки F складывается из двух случайных −максимальной нагрузки спектра и коэффициента вариации режима

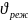
, (49)

в среднем, 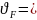0.1…0.15.

Численные значения вероятности безотказной работы определяются по таблице нормального распределения (приложение 4) в зависимости от квантили

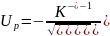, (50)

где - коэффициент запаса по усталостной прочности по средним напряжениям;

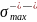среднее значение максимального напряжения цикла, вызванного действием среднего из максимальных значений нагрузок ;

среднее значение предела выносливости детали;

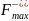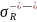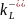-среднее значение коэффициента долговечности

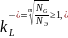( 51)

эквивалентное число циклов перемен напряжений;

коэффициент эквивалентности циклов, равный начальному моменту k-го порядка спектра нагрузок;

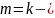показатель степени равный порядку спектра нагрузок. Для нормализованных и улучшенных сталей m=6, из закаленных и сталей с поверхностным упрочнением m=9;

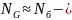число циклов до перелома кривой усталости;

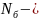базовое число циклов;

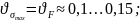
коэффициент вариации предела выносливости детали.

Коэффициент вариации предела выносливости детали определяется по следующей зависимости:

, (52)

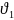
где коэффициент вариации для точного изготовленной детали из материала одной плавки; обычно 0,04…0,1 (определение этого коэффициента на основании теории подобия приводится в следующем разделе 3.5.), подробнее см. ;

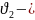коэффициент вариации, учитывающий межплавочное рассеяние, приблизительно равный коэффициенту вариации предела прочности материала 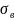, для улучшенных или нормализованных сталей, 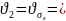0,05…0,07 для сталей с термически упрочненной поверхностью;

(0,3…0,45) коэффициент вариации, учитывающий рассеяние геометрических размеров и шероховатости поверхности концентратора напряжений;

коэффициент вариации радиуса выточки, галтели и другого пересопряжения, являющегося концентратором напряжений.

Более точные значения коэффициентов вариации устанавливаются по справочным материалам.