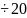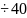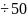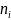2.2.5. Точность и надежность оценок числовых характеристик

случайной величины

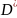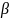Заменяя m и D гипотетического распределения статистическими значениями или или , мы совершаем какую-то ошибку. Интересно оценить эту ошибку и найти вероятность того, что она не превзойдет какого-то значения . Эта величина характеризует точность оценки, а вероятность – её надежность.

Вероятность того, что cтатистическое математическое ожидание откланяется от своего математического ожидания m гипотетического закона распределения не больше, чем

(20)

где Ф(x) – функция Лапласа,

..

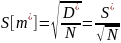Аналогично, вероятность того, что статистическая дисперсия откланяется от D гипотетического закона распределения не больше, чем на

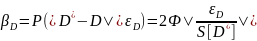, (21)

где S .

2.2.6. Пример выполнения лабораторной работы №1

«Статистическая обработка результатов исследования»

Задание по лабораторной работе №1 индивидуально для каждого студента или группы 2…3 человека приведено в Приложении 3.

По результатам испытаний имеем следующую первичную статистическую совокупность: 52, 47, 21, 28, 31, 38, 33, 41, 54, 48, 22, 27, 32, 37, 34, 42, 55, 13, 23, 26, 33, 36, 43, 44. 35, 34, 24, 14, 51, 15, 25, 35, 34, 45, 46, 33, 36, 26, 16, 17, 27, 37, 32, 31, 38, 28, 18, 29, 39, 32.

1. Cоставляется группированный ряд (таблица 2).

Группированный ряд

Таблица 2

Разряды	10	20	30	40	50
Частоты,	0,12	024	0,4	0,16	0,08
Число попад. в i-й разряд,	6	12	20	8	4
Плотность частоты,	0.012	0.024	0.04	0.016	0.008

2. Строится график функции распределения, пользуясь таблицей 2: F(10)=0; F(20)=0.12; F(30)=0.36; F(40)=0.76; F(50)=0.92; F(60)=1.0. График F(x) приведен на рисунке 3. На рисунке 4. показана гистограмма.

Рисунок 3. Статистическая функция распределения. Рисунок 4. Гистограмма.

3.При определении приближенных значений статистических характеристик 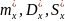по формулам (11), (12), (13) выбирается в качестве «представителя» i-го разряда его середина и этому значению 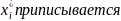частота

Таблица 3.

	15	25	35	45	55
	0.12	0.24	0.4	0.16	0.08

;

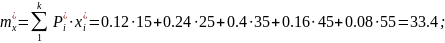
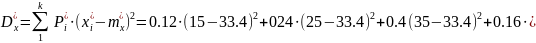Статистические характеристики, определенные по формулам (2), (3), (4):

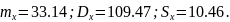
Чем больше число опытных данных и, соответственно, число разрядов (желательно иметь k=12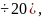 тем меньше различаются статистические характеристики от приближенных значений.

4. При выравнивании эмпирических зависимостей с помощью нормального закона в качестве вероятностных характеристик для данного примера берем: Учитывается еще одна связь

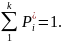
Функция гипотетического закона распределения F(x) будут отражена графиком, изображенном на рисунке 5, и плотность распределения - графиком на рисунке 6.

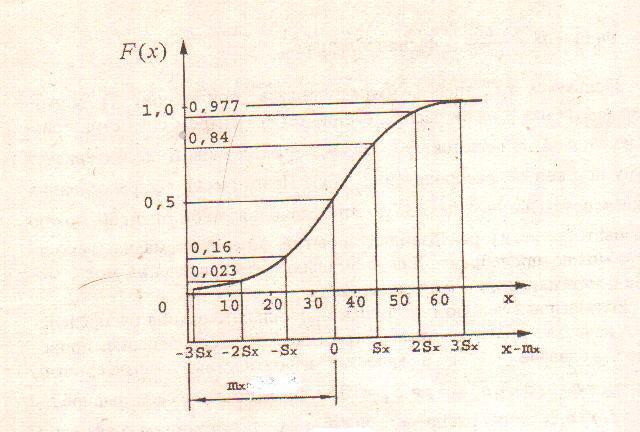
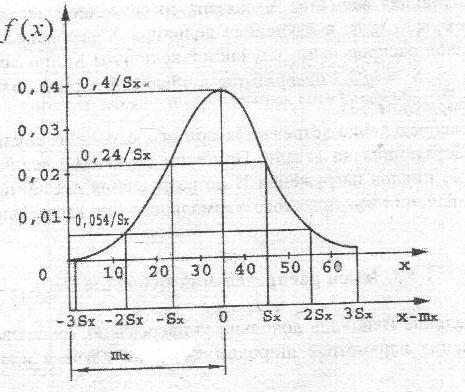
Рисунок 5. График функции распределения. Рис.6. График плотности вероятностей.

5. Требуется установить степень соответствия гипотетического распределения статистическому. Для этого необходимо, в первую очередь, определить критерий согласия Пирсона. Параметр зависит от числа степеней свободы r=k-z= 5-3=2.

Вероятности попадания случайной величины на заданный участок разряда определяем по формуле (19). Для данного примера при имеем: 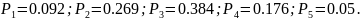Тогда, определяя коэффициент согласия по формуле (18), получим Пользуясь таблицей (Приложение 2), имеем вероятность соответствия гипотетического распределения статистическому, 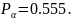Гипотезу можно считать не противоречащей опытным данным для разобранного примера. Вероятность не превышает порог значимости заданный для данного случая.

6. Пусть нас интересует, насколько точно соответствуют количественные характеристики 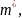характеристикам гипотетического закона m и D , выравнивающего статистическое распределение рассматриваемого примера. Задаются значения По формулам (20), (21) определяем вероятности того, что ошибки не превысят заданных ограничений.

S ;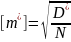

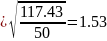S N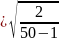  117.43 ;

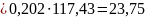Ф

Вероятности того, что ошибки от замены m 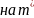не превзойдет 2, а от замены дисперсии D на не превзойдет 20, достаточны, чтобы считать событие практически достоверным.

3. Надежность машин и конструкций

3.1. Основные положения и зависимости надежности

Надежность – свойство объекта сохранять во времени способность к выполнению требуемых функций в заданных режимах и условиях эксплуатации. Принято толковать надежность как комплексное свойство, которое в зависимости от назначения объекта и условий его применения может включать свойства: безотказность, долговечность, сохраняемость и ремонтопригодность или определенные сочетания этих свойств.

Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ не возникает. Вероятность безотказной работы оценивается относительным количеством работоспособных элементов

P(t) 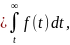(22)

где n – число объектов, отказавших к моменту времени t;

число работоспособных объектов;

N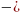 количество объектов;

f(t) 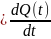– функция плотности распределения вероятностей наработки до отказа;

Q(t) – вероятность отказов.

Вероятность отказов через плотность вероятностей f(t)

Q(t)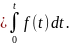 (23)

В расчетах на надежность широко применяется еще один показатель – интенсивность отказов

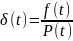. (24)

Если вероятность отказов достаточно мала, интенсивность отказов близка к плотности вероятности. При заданной интенсивности отказов формулу (24) можно считать, как дифференциальное уравнение относительно функции P(t). Решение этого уравнения при начальных условиях P(0)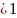 будет

P(t)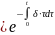 . (25)

В период нормальной эксплуатации машин, когда износовые отказы еще не появляются, надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением обстоятельств и потому имеют постоянную интенсивность, которая не зависит от возраста изделия

(26)

где 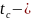средняя наработка на отказ, срок службы.

P(t)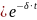 . (27)

Если, как обычно, 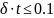, то

P(t) . (28)

Плотность распределения в (общем случае)

f(t) . (29)

Для постепенных (износовых) отказов законы распределения времени безотказной работы дают вначале низкую плотность распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных элементов. Нормальное распределение является наиболее универсальным, удобным и широко применяемым для практических расчетов

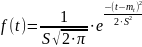, (30)

где математическое ожидание;

S – среднее квадратичное отклонение.

Вероятность отказов и вероятность безотказной работы по формулам (23), (22) через функцию Лапласа выражаются формулами

Q(t)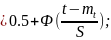 P(t) ( 31)

Определение вероятности безотказной работы P(t) легче производить с помощью таблицы (приложение 4) через квантиль нормированного нормального распределения 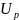. Квантилью называют значение случайной величины, соответствующей заданной вероятности

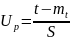. (32)

При заданной вероятности среднее время наработки до отказа

t

При совместном действии внезапных и постепенных отказов вероятность безотказной работы за период t по теореме перемножения вероятностей

P(t)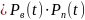 .