
- •1. Понятие качества нового продукта
- •2.2.2. Закон нормального распределения
- •2.2.3. Закон распределения Вейбулла
- •2.2.4. Критерий согласия Пирсона
- •2.2.5. Точность и надежность оценок числовых характеристик
- •3.2. Зависимость надежности системы от надежности элементов
- •3.3. Пример выполнения лабораторной работы № 2
- •3.4. Надежность работы элементов конструкции по критерию усталостной прочности
- •3.5. Применение статистических методов подобия к определению усталостных характеристик деталей машин
- •3.6. Пример выполнения лабораторной работы № 3 «Исследование
- •3.8 . Пример выполнения лабораторной работы №4
2.2.2. Закон нормального распределения
В качестве закона, выравнивающего результаты статистического исследования часто используется закон нормального распределения (закон Гаусса).
Плотность вероятности описывается формулой
f , (14)
, (14)
где
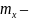 математическое ожидание случайной
величины,
математическое ожидание случайной
величины,
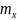 =
=
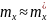 ;
;
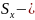 среднее
квадратичное отклонение,
среднее
квадратичное отклонение,
 .
.
Зная выражение f(x), можно определить функцию распределения вероятностей F(x).
F(x)
=
 ,
(15)
,
(15)
где
Ф(x)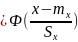 – функция Лапласа (Приложение 1).
– функция Лапласа (Приложение 1).
Пользуясь
таблицей функции Лапласа (Приложение
1) можно легко построить график
распределения F(x). Центром симметрии
распределения f(x)
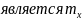 .
Параметр рассеяния
характеризует форму под кривой
распределения f(x). Практически все
случайные величины укладываются на
участке
.
Параметр рассеяния
характеризует форму под кривой
распределения f(x). Практически все
случайные величины укладываются на
участке
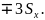 Этой
приближенной оценкой можно пользоваться,
когда реализацией событий, имеющих
малую вероятность можно пренебречь.
Для нормального распределения мода,
медиана и математическое ожидание
равны.
Этой
приближенной оценкой можно пользоваться,
когда реализацией событий, имеющих
малую вероятность можно пренебречь.
Для нормального распределения мода,
медиана и математическое ожидание
равны.
2.2.3. Закон распределения Вейбулла
Распределение
Вейбулла довольно универсально,
охватывает путем варирования параметра
формы
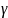 широкий диапазон случаев изменения
вероятностей.
широкий диапазон случаев изменения
вероятностей.
Закон плотностей вероятности
f(x)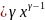 exp
exp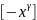 ;
(16)
;
(16)
функция распределения вероятностей
F(x)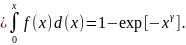 (17)
(17)
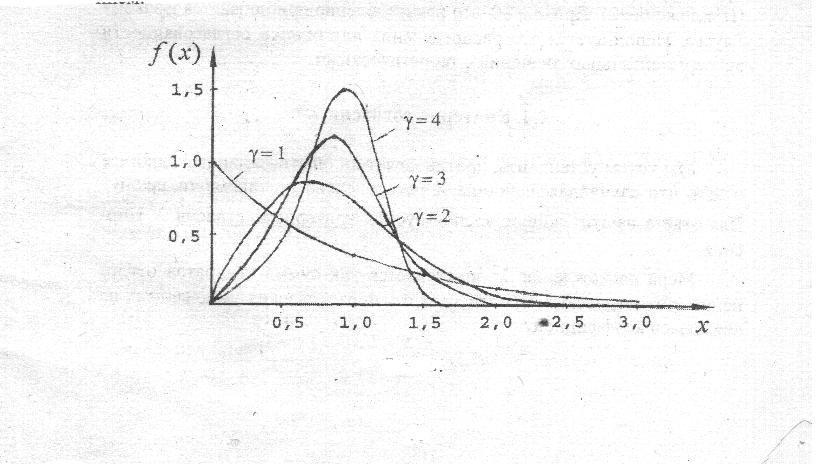
Рисунок 4. Закон распределения плотности вероятностей Вейбулла.
Математическое ожидание и дисперсия случайной величины
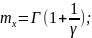
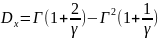 ,
,
где
Г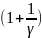 – Гамма – функция Эйлера.
– Гамма – функция Эйлера.
График f(x) для ряда значений показан на рисунке 4.
При
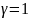 распределение
превращается в экспоненциальное, при
распределение
превращается в экспоненциальное, при
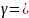 2
распределение соответствует распределению
Релея. Когда параметр формы
заключен в пределах 3,3 … 4,0 распределение
Вейбулла можно аппроксимировать
нормальным распределением.
2
распределение соответствует распределению
Релея. Когда параметр формы
заключен в пределах 3,3 … 4,0 распределение
Вейбулла можно аппроксимировать
нормальным распределением.
2.2.4. Критерий согласия Пирсона
Мы хотим установить, противоречат ли опытные данные гипотезе о том, что случайная величина распределена по такому-то закону? Для ответа на этот вопрос воспользуемся критерием согласия Пирсона.
Мера расхождения определяется как сумма квадратов отклонений статистических вероятностей от гипотетических умноженных на «весовые» коэффициенты.
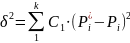 .
.
Весовые
коэффициенты вводятся потому, что
отклонения, относящиееся к разным
значениям вероятности попадания
случайной величины на заданный участок
i – го разряда, нельзя считать равноправными
по значимости. По Пирсону
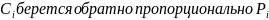
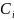
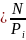 .
.
Заменяя
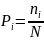 , формула для критерия согласия примет
вид:
, формула для критерия согласия примет
вид:
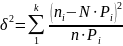 .
(18)
.
(18)
Критерий
зависит от параметра r, называемого
числом «степеней свободы». Число
степеней свободы равно разности между
числом разрядов и числом независимых
«связей» z, наложенных на частоты
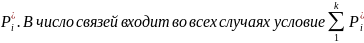
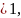 требования
требования
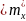 ,
,
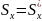 и т.д.
и т.д.
Вероятность попадания случайной величины на заданный участок разряда
 .
(19)
.
(19)
Определив
вероятности попадания событий для всех
разрядов, учитывая, что
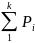 подсчитываем
по формуле (18) критерий согласия
для рассматриваемого примера. По формуле
r
подсчитываем
по формуле (18) критерий согласия
для рассматриваемого примера. По формуле
r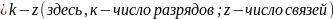 ,
определяем число степеней свободы r.
Пользуясь таблицей (Приложение 2) по r
и
устанавливаем вероятность соответствия
гипотетического распределения
статистическому,
,
определяем число степеней свободы r.
Пользуясь таблицей (Приложение 2) по r
и
устанавливаем вероятность соответствия
гипотетического распределения
статистическому,
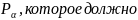 быть выше уровня значимости
быть выше уровня значимости
 При
При
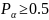 гипотезу
можно считать правдоподобной, при 0,3
гипотезу
можно считать правдоподобной, при 0,3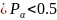 гипотезу можно считать не ротиворечащей
опытным данным. Если вероятность
гипотезу можно считать не ротиворечащей
опытным данным. Если вероятность
 очень мала – гипотеза противоречит
опытным данным.
очень мала – гипотеза противоречит
опытным данным.
