ВВЕДЕНИЕ

Необходимость получения знаний по принципам и методам управления качеством вызвана определяющей ролью качества в обеспечении конкурентоспособности организации, продукции, услугам, что подтверждается опытом, накопленным в нашей стране и во всех развитых странах.

Математический аппарат по анализу качества продукции, услуг, продаж и т.д. называется «Статистическая теория».

Задачей методического указания является коротко и доходчиво изложить основы статистической теории.

Другой задачей является применение этой теории для индивидуального выполнения ряда лабораторных работ по разработанным заданиям.

Студенты должны получить знания по статистической теории, получить навыки по методам её использования при анализе статистического материала.

Знания, полученные при изучении данной дисциплины и выполнении лабораторных работ, будут востребованы в рамках подготовки выпускных работ бакалавров и магистерских диссертаций.

1. Понятие качества нового продукта

Качество – это степень, с которой совокупность собственных характеристик продукта труда выполняет требования.

В дальнейшем продукты труда будем называть продуктами, понимая под этим как материальную продукцию, так и услуги.

Подходы определения качества разнообразны и противоречивы. Иногда встречается определение качества, как отсутствие дефектов.

Качество продукции складывается в процессе разработки, проектирования и производства новой продукции, технологии, услуги. К параметрам качества относятся:

- функциональность (способность эффективно реализовывать свое назначение);

- надежность (долговечность, безотказность);

- технологичность (удобство применения, возможность ремонта);

- унифицированность (наличие стандартных элементов);

- эргономичность (соответствие санитарным и другим нормам);

- эстетичность (презентабельный вид);

- транспортабельность (компактность);

- защищенность патентами; безопасность (безвредность применения);

- экологичность (возможность утилизации);

- экономичность (соотношение качества и цены).

В основе менеджмента качества должен быть заложен процессный и системный подходы контроля качества, при которых достигается более эффективный результат при достижении цели. Менеджмент качества, заложенный в стандартах, показан на рисунке 1.

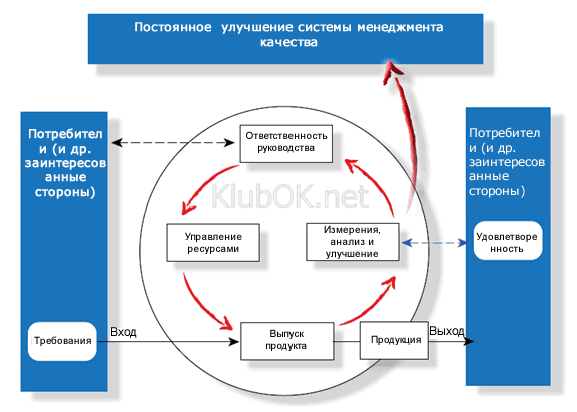
Рисунок 1. Система ИСО – 9000 менеджмента качества.

Для оценки качества продукта используется статистическая теория.

В методическом указании приведены основы статистической теории. Для закрепления теории в лабораторных работах студентами индивидуально или в группе 2…3 человека должна быть выполнена работа по статистической обработке экспериментальных (опытных) данных с поисками замены дискретного распределения непрерывным законом. Должно быть проведено исследование по установлению параметров надежности (вероятность безотказной работы и срока службы) комбинированной системы, в том числе с резервированием ряда подсистем. При известном режиме работы вала по критерию усталостной прочности необходимо установить вероятность его безотказной работы при заданном сроке службы. Установить вероятность безотказной работы системы «вал – ступица» с натягом по критерию сцепления.

2. Статистическая теория

2.1.Общие понятия

Необходимость широкого применения статистических методов на промышленных предприятиях, торговых предприятиях и в сфере услуг определяются основными причинами:

- снижением доли дефектной продукции путем предупреждения образования любых несоответствий;

- требованием международных стандартов ИСО серии 9000, рассматривающих применение статистических методов, как непременный признак существования у поставщиков продукции системы качества и её эффективного функционирования.

В системах управления качеством статистические методы могут решать следующие задачи:

- производить статистическую обработку оперативной информации о качестве продукции;

- осуществлять анализ хода технологического процесса с целью принятия решений о статистическом регулировании;

- оценить результаты сплошного и выборочного контроля и правильность выбора средств контроля;

- организовать эффективный статистический приемочный контроль качества на различных этапах изготовления продукции;

- осуществлять прогнозирование и оценку надежности продукции на этапе ее эксплуатации;

- производить: анализ рынка, маркетинговых исследований, управления продажами и поставками;

- оказывать помощь при проектировании продукции (расчеты допусков, точности геометрических цепей и т. д.).

- определение требований к надежности, прогнозирования долговечности и срока службы;

- оценки безопасности и анализа рисков.

Конкретные статистические методы включают:

- планирование экспериментов и факторный анализ;

- корреляционный анализ и регрессионный анализ;

- критерии значимости;

- карты контроля качества и методы кумулятивных сумм,

- статистический выборочный контроль.

2.2. Статистическая обработка результатов опыта

2.2.1. Определение количественных статистических характеристик

Математическая статистика занимается правилами получения, обработки и истолкования эмпирического распределения случайной величины.

Необходимо ответить на вопросы:

а) как упорядочить поступающий в наше распоряжение статистический материал, какими формами таблиц, графиков лучше всего воспользоваться?

б) как по известному распределению эмпирических частот повторения случайной величины, математическому ожиданию, дисперсии найти соответствующее теоретическое распределение вероятностей?

В) как оценить близость эмпирического и теоретического распределения?

Первое, что попадает в наши руки – «протокол испытаний», в котором зарегистрирован номер опыта «j», и значения случайной величины X. Такой протокол называется первичной статистической совокупностью.

Рассмотрение и осмысливание таблицы такого типа испытаний, где результаты пронумерованы в порядке возрастания, называется упорядоченной статистической совокупностью,

X: .

По упорядоченной статистической совокупности можно построить график статистической функции распределения

F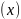 = P , (1)

где F(x) – разрывная ступенчатая функция распределения, равная 0 левее наименьшего наблюдаемого значения и справа - сумме вероятностей событий ;

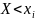P – вероятность событий случайной величины X <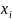 (здесь, – некоторая текущая переменная).

Среднее арифметическое случайной величины X называется статистическим математическим ожиданием

, (2)

где

N – общее число опытов.

Для характеристики разброса значений случайной величины X принимается статистическая дисперсия случайной величины

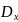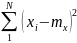= = , (3)

где 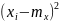– центрированная случайная величина в квадрате.

Для практических расчетов удобнее использовать величину, которая является статистическим средним квадратичным отклонением

. (4)

Чем меньше 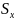, тем теснее группируются значения случайной величины около её среднего значения.

Если результаты экспериментов характеризуется двумя случайными величинами X,Y, то степень зависимости между этими случайными величинами устанавливаются по величине статистичеcкого корреляционного момента

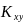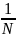
= , (5)

или по коэффициенту корреляции

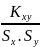= . (6)

Распределение случайных величин дискретного характера можно представить в виде таблиц и графиков. Для составления таблицы устанавливают максимальное и 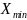минимальное значения и поле рассеяния - 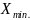. Поле рассеяния делят на равные интервалы случайных величин «а». Их число k определяется из отношения поля рассеяния к избранному значению «а» интервала

k . (7)

Частота попаданий событий в разряд определяется как отношение количества событий, попадающих в разряд, к общему числу событий (событие на границе двух смежных разрядов прибавляется долями по 0,5 для обоих разрядов)

, (8)

причем, = 1.

Плотность частоты каждого разряда

. (9)

Полную картину о законе распределения случайной величины из результатов наблюдений получаем из рассмотрения группированного статистического ряда. Группированным статистическим рядом называется таблица (таблица 1), где в верхней строке указаны разряды, в нижней - соответствующие им частоты.

Статистический группированный ряд

Таблица 1

			. . .		. . .
			. . .		. . .

Имея в своем распоряжении группированный статистический ряд можно построить график закона распределения случайной величины

F (10)

гистограмму (статистический аналог закона распределения плотности вероятностей) (9), определить приближенные статистические характеристики

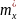
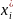; (11)

(12)

, (13)

здесь - «представитель» i-го разряда, его середина и этому значению приписывается частота .

При большом количестве разрядов ; .

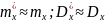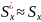На практике часто приходится решать вопрос, как подобрать для данного статистического распределения аналитическую формулу, выражающую существенные черты статистического материала? Такая задача называется задачей выравнивания статистического материала.

При сглаживании эмпирических зависимостей считается, что наилучшим приближением в данном классе функций является то, для которого сумма квадратов отклонений обращается в минимум.