40. Достижимость в сети Петри. См. Билет 29

41. Дерево достижимости в сетях

Определение. Множество достижимости R(C, ) для сети Петри С = (Р, T, I, O) с маркировкой есть наименьшее множество маркировок, определенных следующим образом: 1. 2. Если и для некоторого , то

Проще говоря, множество достижимости – это множество всех состояний(маркировок)сети, достижимых из текущего состояния. Говорят, что состояние 2 достижимо из состояния 1, если есть такой разрешенный переход tj, выполнив который, мы перейдем из состояния 1 в состояние 2.

Напомним, что переход tj разрешен в том случае, когда в любой его входной позиции число фишек не меньше, чем число дуг, идущих от этой позиции к переходу, то есть фишек в любой входной позиции «хватает» для перехода.

Д

P₂

ерево достижимости. Дерево достижимости представляется множеством состояний сети.

Пример:

P₁ t₂ P₃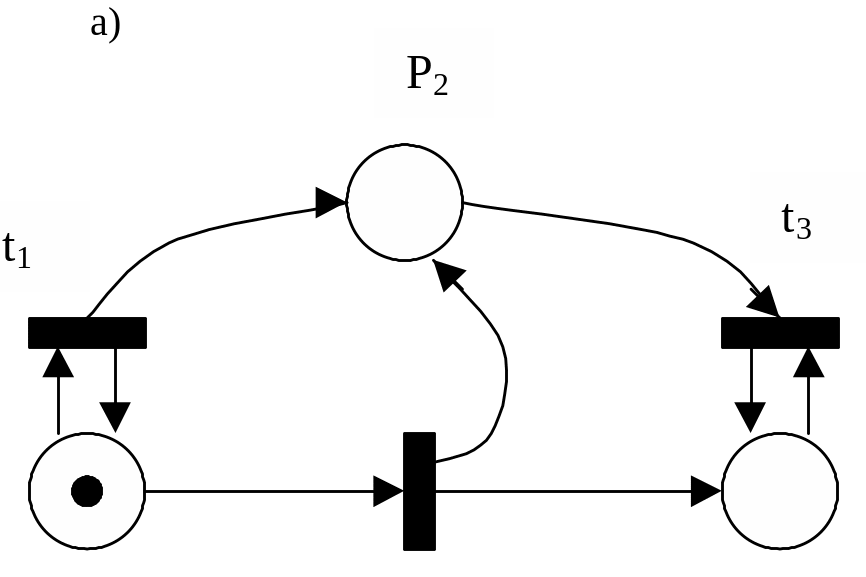

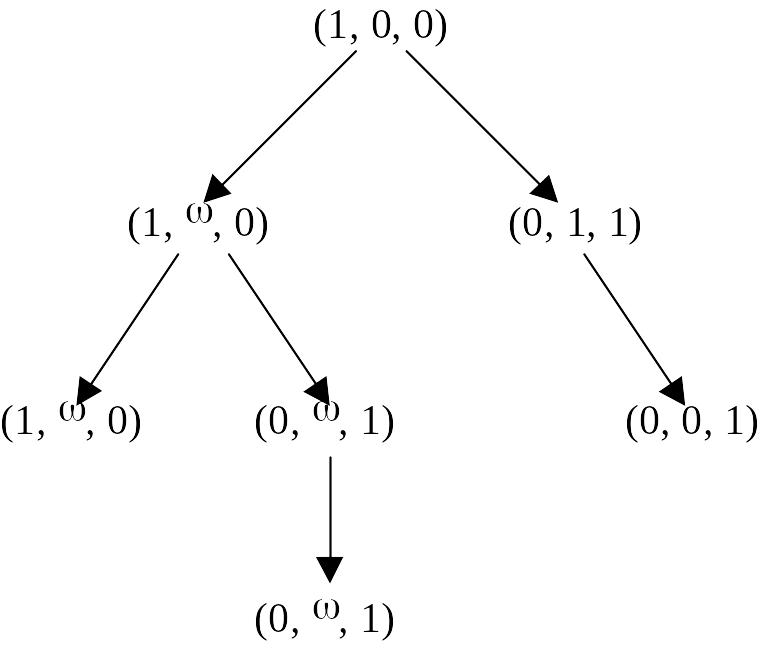
Проверка свойств: безопасность и ограниченность.

Сеть Петри ограниченна тогда и только тогда, когда символ

ω отсутствует в её дереве достижимости.

42. Анализ сетей Петри

С помощью сетей Петри можно моделировать широкий класс систем, пред-

ставляя должным образом взаимодействие различных процессов, которые могут воз-

никнуть в системе. Как отмечалось ранее, наиболее часто сети Петри применяют при

моделировании систем, включающих параллельные действия.

Моделирование системы (устройства) на основе сетей Петри предполагает про-

ведение тщательного анализа, который должен привести к глубокому пониманию по-

ведения моделируемой системы. Таким образом, необходимо рассмотреть методы

анализа и свойства сетей Петри. Для этого рассмотрим типы задач, которые могут

решаться с применением сетей Петри. Цель анализа сети Петри – получение ответа на

вопрос о конкретной сети Петри.

Анализ сетей Петри

Моделирование без анализа малополезно!

Задача анализа сети Петри - определение свойств сети:

• Безопасность

• Ограниченность

• Сохранение

• Активность

• Достижимость и покрываемость

• Эквивалентность

Основными свойствами сети Петри являются:

Ограниченность — число меток в любой позиции сети не может превысить некоторого значения K;

Безопасность — частный случай ограниченности, K=1;

Безопасность важна для моделирования аппаратуры. Без­опасную позицию можно реализовать одним триггером.

Сохраняемость — постоянство загрузки ресурсов, постоянна. Где Ni — число маркеров в i-той позиции, Ai — весовой коэффициент; Переход называется активным, если он не заблокирован, то есть потенциально запустимым.

Свойство сохранения является важным при моделировании распределения ресурсов.

Достижимость — возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;

Живость — возможность срабатывания любого перехода при функционировании моделируемого объекта.

Методы анализа:

• Деревья достижимости

• Матричные уравнения

43,47 Матричные уравнения сетей +